Резонансные режимы в цепях синусоидального тока при последовательном и параллельном соединении приемников

Резонансным режимом в цепях синусоидального тока называется такой режим, при котором сдвиг фаз φ между входным напряжением и током равен нулю, входное сопротивление чисто активное.

В цепи с последовательным соединением элементов R, L, C сдвиг фаз между входным напряжением и током определяется через сопротивления этого участка цепи:

.

Сдвиг фаз становится равным нулю при равенстве реактивных сопротивлений . Напряжения на индуктивном и емкостном элементах равны между собой (рис. 3.6, б), поэтому резонанс в рассматриваемой цепи называют резонансом напряжений. Входное напряжение при этом равно напряжению на активном сопротивлении.

Из условия возникновения резонансного режима следует способ его достижения. Резонанс напряжений в цепи можно получить путем изменения одной из трех величин при постоянстве двух других:

1. f=var, L=const, C=const;

2. f=const, L= var, C=const;

3. f=const, L=const, C= var.

Характеристики, показывающие изменение напряжений, тока и сдвига фаз при изменении одного из параметров, называются резонансными характеристиками.

Рассмотрим резонансные кривые при изменении частоты питающего напряжения (рис. 3.20).

Ток в цепи определяется законом Ома:

При значении частоты ω=0 емкостное сопротивление Х_С равно бесконечности и ток в цепи равен нулю. Далее, с увеличением частоты емкостное сопротивление уменьшается, а индуктивное увеличивается и ток возрастает до максимального значения при резонансе I_p=U/R= max. При дальнейшем увеличении частоты ток уменьшается и при ω→∞, когда индуктивное сопротивление стремится к бесконечности, он стремится к нулю.

напряжение на индуктивности определяется выражением и форма его графика соответствует кривой зависимости тока I(ω).

При ω=0 напряжение на емкости равно сетевому напряжению U, так как сопротивление конденсатора равно бесконечности, ток в цепи отсутствует и все входное напряжение приложено к месту разрыва. При ω=ω_р напряжение на емкостном элементе равно напряжению на индуктивном элементе. При ω→∞ напряжение емкостного элемента стремится к нулю.

В резонансной цепи комплексное сопротивление равно активному сопротивлению и имеет минимальное значение Z=R=min. Тогда ток в такой цепи, как было показано выше, будет иметь максимальное значение:

I_Р =U/z=U/R= I_max.

В случае, если реактивные сопротивления по величине гораздо больше активного сопротивления 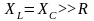, в режиме резонанса напряжения на индуктивном и емкостном элементах могут во много раз превышать входное напряжение:

.

Соотношение напряжений в резонансном режиме определяется величиной добротности Q контура, понятие которой вводится, исходя из следующих соображений:

,

где Q – добротность цепи, состоящей из последовательно соединенных элементов R, L, C , значение которой может достигать десятков и сотен единиц.

При изменении частоты от 0 до ω_р угол сдвига фаз φ между напряжением и током изменяется от (-π/2) до 0. При изменении частоты от ω_р до ∞ угол φ возрастает от 0 до π/2.

При параллельном соединении элементов R, L, C угол сдвига фаз между входным напряжением и током в цепи определяется выражением:

.

Рис. 3.20

Сдвиг фаз будет равен нулю при равенстве реактивных составляющих проводимостей: или , что и будет являться условием резонанса токов. Так как равны реактивные составляющие проводимостей , токи индуктивного I_L=b_LU и емкостного I_C=b_CU элементов равны, поэтому этот резонансный режим называют резонансом токов. Реактивные токи находятся в противофазе и их сумма равна нулю. В этом случае входной ток будет равен току активного элемента и иметь минимальное значение I= I_R=gU= min.

Резонансные кривые (рис. 3.21) для режима резонанса токов строятся аналогично резонансным кривым, построенным для режима резонанса напряжений.

Рис. 3.21

Входной ток цепи определяется согласно первому закону Кирхгофа:

Ток активного сопротивления от частоты питающего напряжения не зависит и будет всегда неизменным.

При частоте равной нулю ток емкости равен нулю, так как конденсатор представляет собой разомкнутый участок цепи, а ток идеальной катушки стремится к бесконечности, так как при нулевой частоте катушки представляет собой короткозамкнутый участок. Входной ток при этой частоте равен току катушки и также стремится к бесконечности.

При частоте равной резонансной ω_рез действующие значения емкостного и индуктивного токов равны. А так как эти токи находятся в противофазе, то их векторная сумма равна нулю и входной ток равен току активного элемента и имеет минимальное значение.

При дальнейшем увеличении частоты проводимость емкостного элемента увеличивается, а проводимость индуктивного элемента уменьшается. Входной ток увеличивается за счет возрастания реактивной составляющей.

При частотах меньше резонансной ω<ω_рез угол сдвига фаз больше нуля φ>0, так как преобладает индуктивная составляющая проводимости. При частоте равной резонансной ω=ω_рез реактивные составляющие проводимостей равны и угол сдвига фаз равен нулю φ=0. При частотах больше резонансной ω>ω_рез угол сдвига фаз меньше нуля φ<0 и стремится к значе нию -π/2, так как преобладает емкостная составляющая проводимости.