Параллельное соединение реальной индуктивной катушки и конденсатора

На рис. 3.12 представлена схема параллельного соединения реальной индуктивной катушки с параметрами L_К, R_К и идеального конденсатора с емкостью С.

Для действующих комплексных значений токов на основании первого закона Кирхгофа запишем:

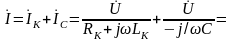
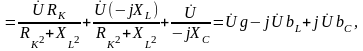
где активная и реактивные составляющие проводимостей находятся:

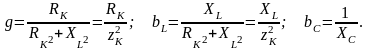
Ток реальной индуктивной катушки представлен как сумма активной составляющей, совпадающей по фазе с напряжением, и реактивной составляющей отстающей от напряжения по фазе на угол 90º:

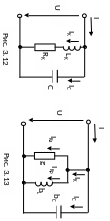
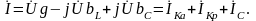
В этом случае на схеме замещения реальную индуктивную катушку можно представить в виде параллельного соединения двух ветвей с активной и реактивной проводимостями (рис. 3.13).

Заметим, что в случае, если ветвь содержит не один, а несколько элементов, активная и реактивная составляющие полной проводимости такой ветви будут определяться:

, .

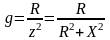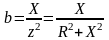Комплексная проводимость схемы рис. 3.12

.

В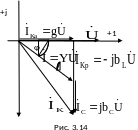 екторная диаграмма токов и напряжений (рис. 3.14) будет аналогична векторной диаграмме параллельного соединения идеальных элементов R, L, C.

Схемы замещения реальной индуктивной катушки и конденсатора

С помощью идеальных элементов R, L, C можно составить схемы замещения реальных элементов.

Так, катушка индуктивности с током I_К, напряжением U_К и углом сдвига фаз между ними φ_К на схеме замещения может быть представлена в виде последовательного (рис. 3.15, а) или параллельного (рис. 3.15, б) соединений активного и индуктивного элементов. Векторные диаграммы токов и напряжений для этих схем проведены соответственно на рис 3.16, а и б.

П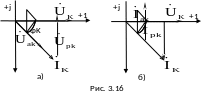 араметры схем замещения определяются следующим образом.

Для последовательной цепи:

Активная и реактивная составляющие напряжения и сопротивления катушки

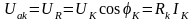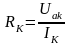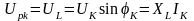, тогда ;

, тогда .

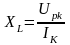Для параллельной цепи:

Активная и реактивная составляющие тока и проводимости катушки

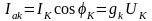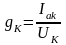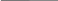
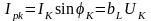, тогда ,

, тогда .

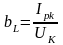При этом параметры последовательной и параллельной схем замещения связаны соотношениями

, ,

, .

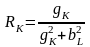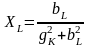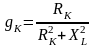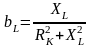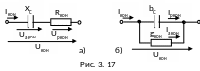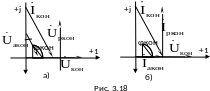К онденсатор с потерями в диэлектрике с током I_КОН, напряжением U_КОН и углом сдвига фаз между ними φ_кон на схеме замещения может быть представлена в виде последовательного (рис. 3.17, а) или параллельного (рис. 3.17, б) соединений активного и емкостного элементов.

Векторные диаграммы токов и напряжений для этих схем проведены соответственно на рис 3.18, а и б.

Параметры схем замещения определяются следующим образом.

Для последовательной цепи:

Активная и реактивная составляющие напряжения и сопротивления конденсатора

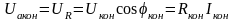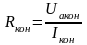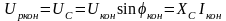, тогда ;

, тогда .

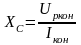Для параллельной цепи:

Активная и реактивная составляющие тока и проводимости конденсатора

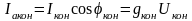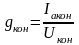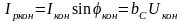, тогда ,

, тогда .

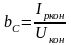При этом параметры последовательной и параллельной схем замещения связаны соотношениями

, ,

, .

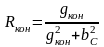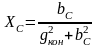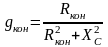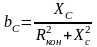Определение параметров пассивного двухполюсника опытным путем

Параметры пассивных двухполюсников можно определить опытным путем с помощью амперметра, вольтметра и фазометра.

Определим параметры индуктивной катушки, представленной на схеме замещения последовательным соединением активного и индуктивного элементов. Для того чтобы определить активное сопротивление катушки R_к и ее индуктивность L_к, катушку и измерительные приборы подключают к сети переменного тока согласно схеме, показанной на рис. 3.19.

Определив по приборам действующие значения напряжения на зажимах цепи U, тока I и с помощью фазометра угол сдвига фаз φ_к между ними, рассчитаем модуль полного сопротивления катушки, а также его активную и реактивную составляющие.

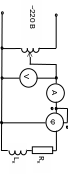
Рис. 3.19

Из треугольника сопротивлений (рис. 3.9) можно легко получить формулы для их определения:

полное сопротивление

активное сопротивление катушки

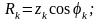
реактивное сопротивление катушки

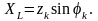
Так как X_L = ωL=2πf, то индуктивность катушки определяется:

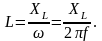
Аналогичным образом можно определить параметры схемы замещения конденсатора. Но так как потери в диэлектрике на низкой частоте невелики, то в данной лабораторной работе конденсатор будем считать идеальным с заданной емкостью С.