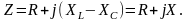- •Линейные элементы r, l, c в цепи синусоидального тока
- •Последовательное соединение элементов r, l, c
- •Векторные диаграммы для цепи с последовательным соединением элементов r, l, c
- •Активная, реактивная и полная мощности. Комплексная мощность. Понятие коэффициента мощности
- •Параллельное соединение элементов r, l, c
- •Параллельное соединение реальной индуктивной катушки и конденсатора
- •Схемы замещения реальной индуктивной катушки и конденсатора
- •Определение параметров пассивного двухполюсника опытным путем
- •Резонансные режимы в цепях синусоидального тока при последовательном и параллельном соединении приемников
- •Описание лабораторной установки
- •Задание на подготовительную работу
- •Программа работы
- •1. Определение параметров индуктивной катушки rk, lk:
- •Построение векторных диаграмм по опытным данным
Последовательное соединение элементов r, l, c
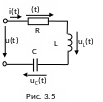
Пусть в цепи, состоящей из последовательно соединенных элементов R, L, C (рис. 3.5), известен ток i(t)=Imsin(ωt + ψi) и необходимо определить напряжение на ее зажимах.
Запишем для цепи уравнение по второму закону Кирхгофа для мгновенных значений напряжений:
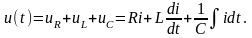 Сумме
синусоидальных напряжений соответствует
сумма изображающих их комплексных
величин. Тогда для действующих комплексных
значений можно записать
Сумме
синусоидальных напряжений соответствует
сумма изображающих их комплексных
величин. Тогда для действующих комплексных
значений можно записать
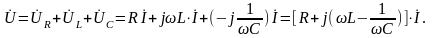 Запишем
комплексное действующее значение
напряжения
Запишем
комплексное действующее значение
напряжения
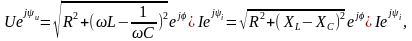
где
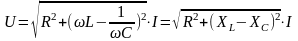 - действующее значение напряжения,
приложенного к цепи;
- действующее значение напряжения,
приложенного к цепи;
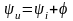 - начальная фаза
напряжения;
- начальная фаза
напряжения;
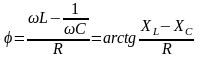 - угол сдвига фаз
между напряжением на зажимах цепи и
током; сдвиг фаз определяется соотношением
реактивных и активных сопротивлений,
включенных в электрическую цепь.
- угол сдвига фаз
между напряжением на зажимах цепи и
током; сдвиг фаз определяется соотношением
реактивных и активных сопротивлений,
включенных в электрическую цепь.
Так как амплитудные значения тока и напряжения связаны с действующими значениями соотношениями
, ,
то амплитудное значение входного напряжения
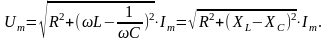
Запишем мгновенное значение напряжения на входе цепи, которое при синусоидальном токе также будет изменяться по синусоидальному закону:
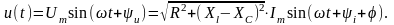
Введем ряд величин, характеризующих цепь синусоидального тока.
Величину
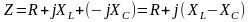
называют комплексным сопротивлением цепи с последовательным соединением элементов R, L, C. Заметим, что в этом случае комплексные сопротивления отдельных участков цепи складываются, как и сопротивления цепи постоянного тока.
Запишем комплексное сопротивление в показательной форме:
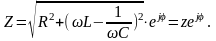
Модуль комплексного сопротвления
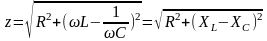 называют полным
сопротивлением цепи.
называют полным
сопротивлением цепи.
Аргумент комплексного сопротивления
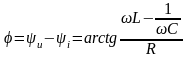 - угол сдвига фаз
между входным напряжением и током.
- угол сдвига фаз
между входным напряжением и током.
При
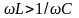 угол φ>0, ток отстает по фазе от
напряжения. При
угол φ>0, ток отстает по фазе от
напряжения. При
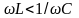 угол φ <0, ток опережает напряжение по
фазе. При
угол φ <0, ток опережает напряжение по
фазе. При
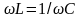 угол φ=0, ток совпадает по фазе с напряжением
и цепь ведет себя как чисто активное
сопротивление. Такой режим работы цепи
называют резонансным.
угол φ=0, ток совпадает по фазе с напряжением
и цепь ведет себя как чисто активное
сопротивление. Такой режим работы цепи
называют резонансным.
Векторные диаграммы для цепи с последовательным соединением элементов r, l, c
В цепи с последовательным соединением элементов R, L, C ток во всех участках один и тот же, а напряжения связаны между собой вторым законом Кирхгофа. В комплексной или векторной форме можно записать
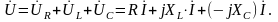
 В
соответствии с тремя возможными
вариантами соотношения между реактивными
сопротивлениями XL
и XC
(XL>XC,
XL<XC,
XL =
XC)
построим три векторные диаграммы для
каждого из случаев (рис. 3.6, а, б, в).
В
соответствии с тремя возможными
вариантами соотношения между реактивными
сопротивлениями XL
и XC
(XL>XC,
XL<XC,
XL =
XC)
построим три векторные диаграммы для
каждого из случаев (рис. 3.6, а, б, в).
При построении
векторных диаграмм примем начальную
фазу тока равной нулю, ψi=0.
Тогда сдвиг фаз φ между входным
напряжением и током и начальная фаза
входного напряжения ψu
будут равны друг другу. Напряжение
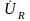 на
активном сопротивлении совпадает по
фазе c током, напряжение
на индуктивном элементе
на
активном сопротивлении совпадает по
фазе c током, напряжение
на индуктивном элементе
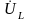 опережает
ток на 90°, напряжение на емкостном
элементе
опережает
ток на 90°, напряжение на емкостном
элементе
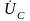 отстает от тока по фазе на 90°.
отстает от тока по фазе на 90°.
Как известно, на
векторных диаграммах угол сдвига фаз
φ отсчитывается от вектора тока
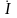 к вектору напряжения
к вектору напряжения
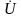 .
Угол φ положителен при отстающем токе
(рис. 3.6, а) и отрицателен при опережающем
токе (рис. 3.6, в).
.
Угол φ положителен при отстающем токе
(рис. 3.6, а) и отрицателен при опережающем
токе (рис. 3.6, в).
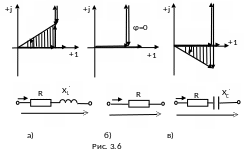
При неизменной частоте источника питания цепь рис. 3.5 может быть представлена одной из эквивалентных схем, представленных на рис. 3.6, а, б, в: при XL>XC как последовательное соединение активного и индуктивного сопротивлений (R и XL´=XL-XC); при XL=XC как активное сопротивление R; при XL<XC как последовательное соединение активного и емкостного сопротивлений (R и XС´=XL-XC).
Заштрихованные
треугольники, показанные на векторных
диаграммах, принято называть треугольниками
напряжений. Проекцию вектора напряжения
на направление вектора тока называют
активной составляющей напряжения и
обозначают
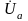 .
Проекцию вектора напряжения на
направление, перпендикулярное вектору
тока, называют реактивной составляющей
напряжения и обозначают
.
Проекцию вектора напряжения на
направление, перпендикулярное вектору
тока, называют реактивной составляющей
напряжения и обозначают
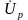 .
Из векторных диаграмм рис. 3.6 видно, что:
.
Из векторных диаграмм рис. 3.6 видно, что:
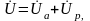
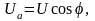
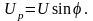
Необходимо заметить, что напряжения на L и С - элементах находятся в противофазе, вследствие чего в цепи переменного тока с последовательным соединением элементов могут создаваться условия, невозможные для цепей постоянного тока, когда напряжения на отдельных участках цепи значительно превышают напряжение на входе.
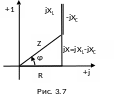 Если
каждую сторону треугольника напряжений
(рис. 3.6, а) поделить на вектор тока, то
получим треугольник, подобный исходному
и называемый треугольником
сопротивлений (рис. 3.7).
Если
каждую сторону треугольника напряжений
(рис. 3.6, а) поделить на вектор тока, то
получим треугольник, подобный исходному
и называемый треугольником
сопротивлений (рис. 3.7).
Этот же треугольник можно получить, построив на комплексной плоскости диаграмму, соответствующую выражению комплексного сопротивления: