1.3.3. Кривые второго порядка на плоскости
Общее уравнение кривой второго порядка на плоскости имеет вид:
.
Любая кривая второго порядка – это либо эллипс (частный случай – окружность), либо гипербола, либо парабола.
Если
в уравнении
,
то оно преобразуется выделением полных
квадратов:
и после введения соответствующих обозначений приводится к одному из следующих видов:
1.
– уравнение эллипса с центром в точке
и полуосями а
и b
(рис. 11).
Рис. 11.
Если
,
то получаем окружность радиуса R
с центром в точке
.
2.
– уравнение определяет гиперболу с
центром в точке М0
.
Для знака плюс, например, точки
,
– вершины гиперболы (рис. 12).
Рис. 12.
Гипербола
имеет две асимптоты:
.
3.
Если
или
,
то получается уравнение параболы,
например, для
:
.
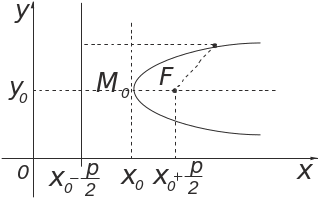
Рис.13.
Точка
называется фокусом параболы, а прямая
называется директрисой параболы
(рис. 13).
Кроме указанных, возможны некоторые вырожденные случаи (когда уравнение определяет пару пересекающихся, параллельных или совпадающих прямых) и мнимые случаи.
Пример
1.9.
Составить уравнение и построить линию,
расстояния каждой точки которой от
точки A(0;–2)
и от прямой
относятся как 4:5.
Решение.
Возьмем точку
на искомой кривой. Тогда точка К,
лежащая на прямой
,
имеет координаты
(МК
– расстояние от М
до прямой).
Рис. 14.
Из условия задачи известно, что АМ:МК=4:5.
Используя формулу для вычисления расстояния между двумя точками, получим
.
Решим это уравнение:
,
,
,
,
,
.
Получили
каноническое уpавнение
эллипса с центром в точке
.
Полуоси эллипса:
,
(рис.15).
Рис. 15.
§1.4. Комплексные числа
Комплексным
числом
называется выражение вида:
,
(алгебраическая
форма числа z),
где x
и y
– вещественные числа, i
– мнимая
единица,
определяемая условием
.
Re
– называется вещественной частью числа
z,
Im
мнимой частью z.
Число
называется сопряженным
к z.
Если
,
,
то
.
.
При
делении двух комплексных чисел следует
числитель и знаменатель умножить на
– число, сопряженное к знаменателю.
Число
r
(рис. 16)
называется модулем
комплексного числа
z
и обозначается
:
.
Угол
называется аргументом
комплексного числа
z
и обозначается Аrg
,
при этом
.
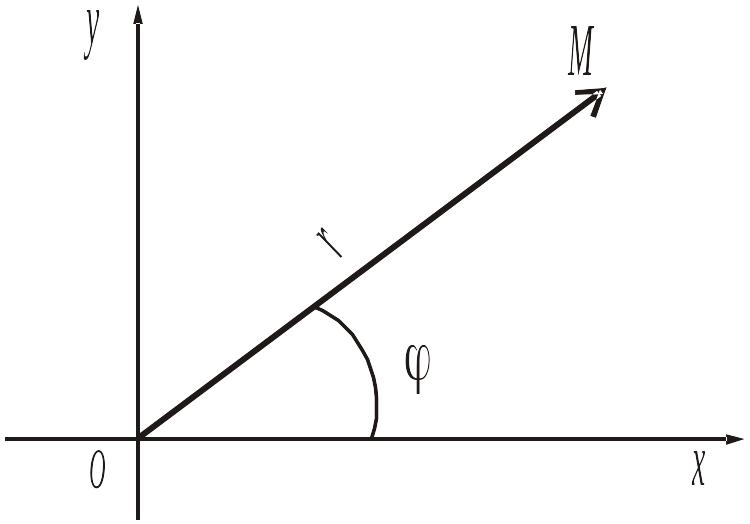
Рис. 16.
Аргумент
определяется неоднозначно, с точностью
до слагаемого, кратного 2:
,
где
– главное
значение
аргумента.
поэтому необходимо учитывать следующие
соотношения:
при
x
0 ;
при
x
0,
y
0 ;
при
x
0,
y
0.
Так
как
,
то комплексное число z
можно представить в виде:
.
Такая запись называется тригонометрической формой комплексного числа z.
Если
заданы два комплексных числа в
тригонометрической форме
и
,
то
,
,
Корнем
n-ой
степени из комплексного числа
z
называется такое комплексное число
,
что
Обозначение
для корня:
.
Корень n-ой
степени из числа
имеет
n
различных значений, определяемых по
формуле:
,
.
Геометрически
числа
располагаются в вершинах правильного
n-угольника,
вписанного в круг радиуса
с центром в начале координат.
Пример
1.10.
Дано комплексное число
1) Записать число z в алгебраической и тригонометрической формах.
2)
Найти
.
Решение.
1)
алгебраическая
форма.
Так
как число z
находится в 4-й четверти, то
Таким образом, тригонометрическая форма числа z:
2)
где k принимает значения 0, 1, 2.
При
.
При
.
При
.