§1.2. Векторная алгебра

1.2.1. Основные определения

Вектором называется направленный отрезок. Длина этого отрезка называется длиной вектора и обозначается через . В векторной алгебре рассматриваются свободные векторы (вектор можно переносить параллельно самому себе из одной точки в другую). Если вектор задан началом A и концом B, то его обозначают через

Суммой векторов и называется вектор построенный с помощью правила треугольника по векторам и (рис.1).

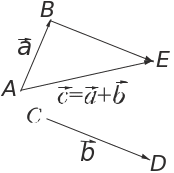
Рис. 1.

Произведением вектора на число называется вектор лежащий на той же прямой, что и вектор (или на прямой, параллельной ей), имеющий длину и то же направление, что и , если , и противоположное, если

Если дана декартова система координат Oxyz, то единичные вектора направленные по осям координат, называются ортами (рис. 2).

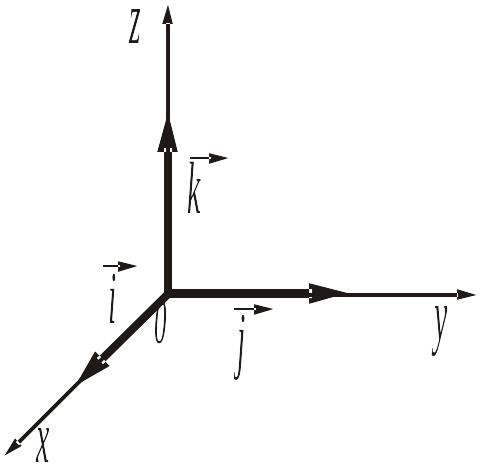
Рис. 2.

Любой вектор единственным образом раскладывается по ортам

Числа называются координатами вектора в базисе Можно использовать более короткую запись:

.

Если и , то

Координатами точки M называются координаты ее радиус-вектора (рис. 3).

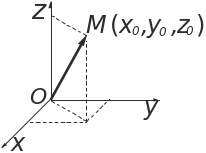
Рис. 3.

Если даны две точки и , то вектор имеет координаты

.

где – угол между векторами и

1.2.2. Скалярное произведение векторов

Скалярным произведением векторов и называется число, определяемое формулой

где – угол между векторами и

Свойства скалярного произведения

1) то есть

2) или или .

3) .

4)

5)

Если и , то

Длина вектора вычисляется по формуле

Расстояние между точками и равно    

Угол между векторами и вычисляется по формуле

1.2.3. Векторное произведение векторов

Векторным произведением векторов и называется такой вектор что

1) где – угол между векторами и .

2) и

3) Вектора , и образуют правую тройку векторов (рис. 4).

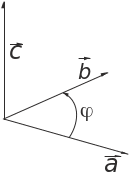
Рис.4.

Свойства векторного произведения

1)

2) или или .

3)

4) .

Если и , то векторное произведение можно вычислить по формуле

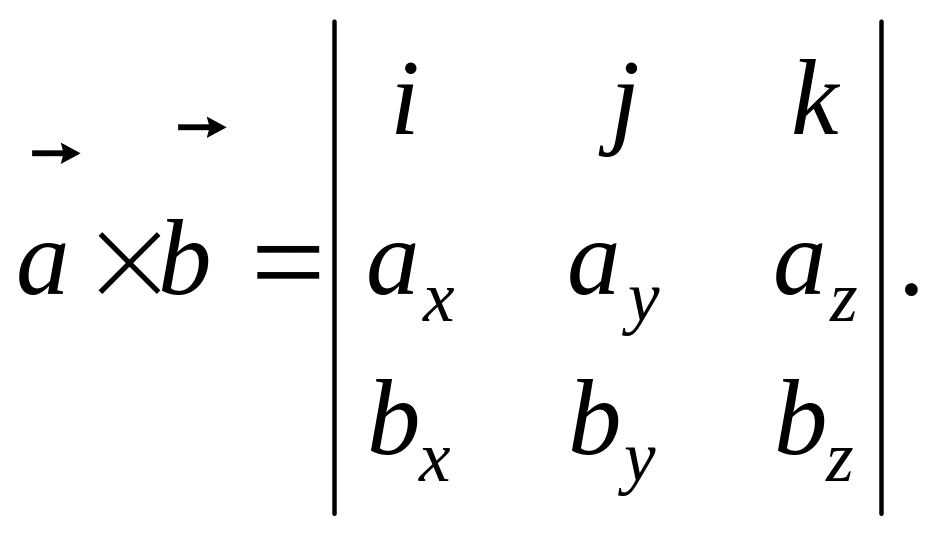
Площадь параллелограмма, построенного на векторах и , равна модулю векторного произведения:

Площадь треугольника, заданного вершинами

, и

в пространстве Оxyz – это половина площади параллелограмма, построенного на векторах и (рис. 5), поэтому

.

Рис. 5.

Площадь треугольника, заданного на плоскости Оxy вершинами , и , равна

.

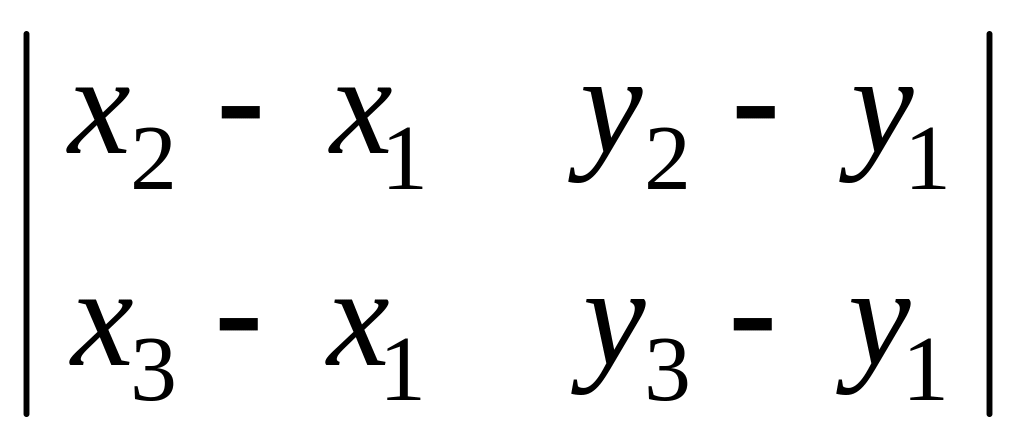1.2.4. Смешанное произведение

Смешанным произведением трех векторов , , называется число .

Свойства смешанного произведения

1)

2) или или либо вектора , и компланарны (лежат в одной плоскости).

Если , , то вычисляется по формуле

.

Объем параллелепипеда, построенного на векторах , и , равен модулю смешанного произведения этих векторов:

V_{параллелепипеда}=

Объем пирамиды, построенной на векторах , и , равен одной шестой модуля смешанного произведения, то есть

_{пирамиды} .