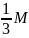- •Курсовая работа
- •Кейс-задание 1 Ситуация 1
- •Ситуация 2
- •1.Составить математическую модель планирования производства, записав соответствующую задачу злп в стандартном виде. Указать смысл всех используемых обозначений и математических выражений.
- •Кейс-задание 2
- •Кейс-задание 3
- •Решение методом потенциалов (наименьшая стоимость)
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Государственное образовательное учреждение
высшего профессионального образования
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ»
(МИИТ)
Институт экономики и финансов
Кафедра «Математика»
Курсовая работа
По дисциплине «Методы оптимальных решений»
Выполнил: студент
Петровский Александр Ильич
группа ЭЭС-211
Проверил : Кекух
Оценка:______________
Москва – 2014
Оглавление
КЕЙС-ЗАДАНИЕ 1 3
Ситуация 1 3
Ситуация 2 7
КЕЙС-ЗАДАНИЕ 2 11
КЕЙС-ЗАДАНИЕ 3 18
Кейс-задание 1 Ситуация 1
Сырье |
Продукция |
Запасы сырья |
||
Р1 |
Р2 |
|||
S1 |
9 |
8 |
66 |
|
S2 |
9 |
4 |
48 |
|
S3 |
3 |
2 |
18 |
|
Прибыль |
7 |
5 |
|
|
ТРЕБУЕТСЯ:
1.Составить математическую модель планирования производства, записав соответствующую задачу ЗЛП в стандартном виде. Указать смысл всех используемых обозначений и математических выражений.
bi ( i = 1,2,3,...,m) — запасы каждого i-го вида ресурса;
aij ( i = 1,2,3,...,m; j=1,2,3,...,n) — затраты каждого i-го вида ресурса на производство единицы объема j-го вида продукции;
cj ( j = 1,2,3,...,n) — прибыль от реализации единицы объема j-го вида продукции.
Пусть
![]() –
количество видов продукции Р1
и P2
соответственно, планируемое к выпуску
(
–
количество видов продукции Р1
и P2
соответственно, планируемое к выпуску
(![]() ,
,
![]() ).
).
Тогда прибыль составит: 7х1+5х2, поскольку план производства должен обеспечивать наибольшую прибыль, то целевая функция задачи: F=7х1+5х2→max
Составим
систему ограничений, используя заданную
ограниченность сырья. При планируемых
объемах производства расходуется сырья
I вида:
9х1+8х2,
что не должно превышать запас 66 ед., и
получаем неравенство: 9х1+8х2 66
66
Составляя неравенства по каждому виду сырья, получим систему:
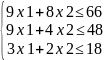
Тогда математическая модель задачи линейного программирования имеет вид:
F=7х1+5х2→max
2.Записать ЗЛП в каноническом виде:
F=7х1+5х2→max

3. Изобразить графически множество допустимых планов для задачи, записанной в стандартном виде.
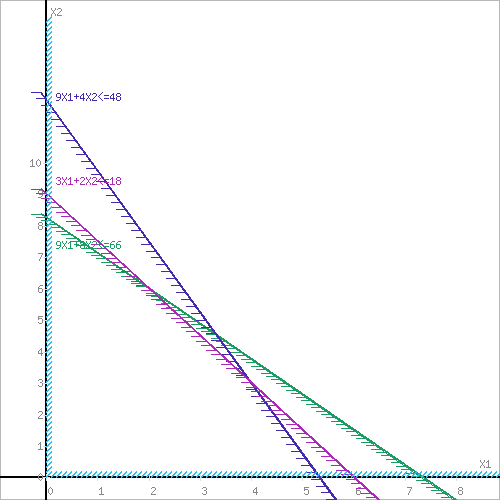
gradF=(7;5)
4.Найти графическим методом оптимальный план выпуска продукции.
 Ответ:
координаты максимальной точки B
(6;2)
F(X) = 7*6+5*2 = 42+10 = 52
Ответ:
координаты максимальной точки B
(6;2)
F(X) = 7*6+5*2 = 42+10 = 52
5. Excel
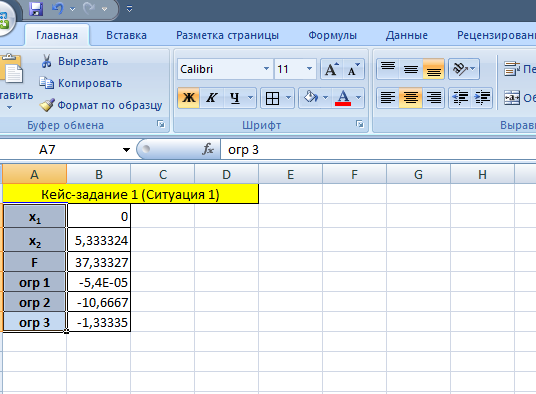
Ситуация 2
Сырье |
Продукция |
Запасы сырья |
|||
P1 |
P2 |
P3 |
|||
S1 |
4 |
6 |
1 |
32 |
|
S2 |
6 |
4 |
1 |
32 |
|
S3 |
2 |
2 |
1 |
12 |
|
Прибыль |
4 |
7 |
1 |
|
|
ТРЕБУЕТСЯ:
1.Составить математическую модель планирования производства, записав соответствующую задачу злп в стандартном виде. Указать смысл всех используемых обозначений и математических выражений.
Известны:
bi ( i = 1,2,3,...,m) — запасы каждого i-го вида ресурса;
aij ( i = 1,2,3,...,m; j=1,2,3,...,n) — затраты каждого i-го вида ресурса на производство единицы объема j-го вида продукции;
cj ( j = 1,2,3,...,n) — прибыль от реализации единицы объема j-го вида продукции.
Требуется составить план производства продукции, который обеспечивает максимум прибыли при заданных ограничениях на ресурсы (сырье).
Введем вектор переменных X=(X1, X2,...,Xn), где xj ( j = 1,2,...,n) — объем производства j-го вида продукции.
Затраты
i-го вида ресурса на изготовление данного
объема xj
продукции равны aijxj,
поэтому ограничение на использование
ресурсов на производство всех видов
продукции имеет вид:
![]() Прибыль
от реализации j-го вида продукции равна
cjxj
, поэтому целевая функция равна:
Прибыль
от реализации j-го вида продукции равна
cjxj
, поэтому целевая функция равна:
![]()
Математическая модель имеет вид:
F=4x1+7x2 + x3→max

2. Привести задачу к каноническому виду.
F=4x1+7x2 + x3→max

х3 12-2х1-2х2
12-2х1-2х2

F=4x1+7x2+12-2х1-2х2 => F=2x1+5x2+12→max
3.Найти графическим методом оптимальный план выпуска продукции.
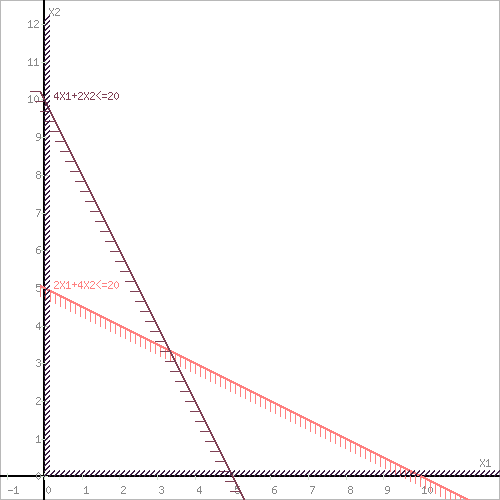
gradF = (2;5)

Ответ: координаты максимальной точки B( 0;5) F(X) = 2*0 + 5*5 + 12 = 37
3.Привести задачу к каноническому виду.
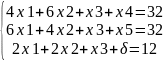
4.Найти решение полученной задачи симплекс-методом.
F=
-4x1-7x2-x3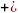 M
M 4x1+7x2
+
x3
M(12-2х1-2х2-х3)
(-4-2M)x1+(-7-2M)x2
+(-1-M)x3+12M
4x1+7x2
+
x3
M(12-2х1-2х2-х3)
(-4-2M)x1+(-7-2M)x2
+(-1-M)x3+12M
БП |
X1 |
X2 ٧ |
X3٧٧ |
X4 |
X5 |
|
СЧ |
Q |
X4 |
4 |
6 |
1 |
1 |
0 |
0 |
32 |
51/3 |
X5 |
6 |
4 |
1 |
0 |
1 |
0 |
32 |
8 |
|
2 |
2 |
1 |
0 |
0 |
1 |
12 |
6 |
F |
-4-2M |
-7-2M |
-1-M |
0 |
0 |
0 |
-12M |
|
X2 |
2/3 |
1 |
1/6 |
1/6 |
0 |
0 |
16/3 |
32 |
X5 |
10/3 |
0 |
1/3 |
-2/3 |
1 |
0 |
32/3 |
32 |
|
2/3 |
0 |
2/3 |
-1/3 |
0 |
1 |
4/3 |
2 |
F |
|
0 |
|
-7/6+M |
0 |
0 |
37 |
|
X2 |
1/2 |
1 |
0 |
1/4 |
0 |
-1/4 |
5 |
|
X5 |
3 |
0 |
0 |
-1/2 |
1 |
-1/2 |
10 |
|
X3 |
1 |
0 |
1 |
-1/2 |
0 |
-1/2 |
2 |
|
F |
1/2 |
0 |
0 |
1*1/4 |
0 |
-1/4+М |
37 |
|
Оптимальный план можно записать так: x2 = 5 x3 = 2 F(X) = 7*5 + 1*2 = 37
6. Excel
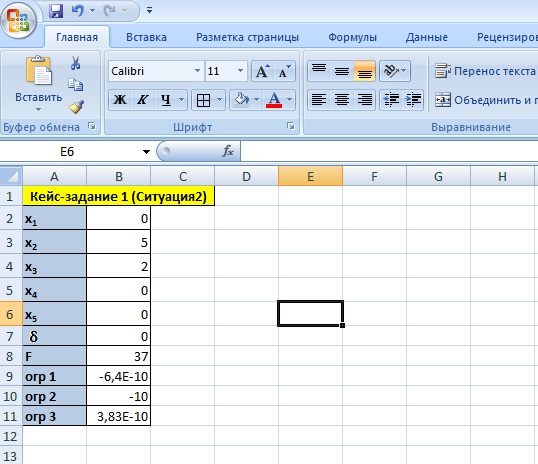
7. Анализ результатов
Предприятию «P1 & P2» не выгоден переход от старой программы к новой, т.к прибыль уменьшилась.


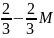
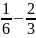 M
M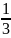 - 1
- 1