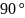- •Вступ.....................................................................................................................3
- •Самоосвітня діяльність учнів та її структура
- •Мета засвоєння стереометрії у шкільній підготовці учнів
- •Організація самоосвітньої діяльності школярів під час опанування стереометрії
- •Мета засвоєння стереометрії у шкільній підготовці учнів.
- •Організація самоосвітньої діяльності учнів під час опанування стереометрії.
- •Теоретична частина підготовки електронного підручника.
- •Дидактичні матеріали.
Мета засвоєння стереометрії у шкільній підготовці учнів.
Повсякденне життя людини, побут, професійна діяльність і вся навколишня природа пов’язані з просторовими геометричними об’єктами: призмами, пірамідами, конусами, циліндрами, кулями та їх комбінаціями. Часто виникає практична необхідність визначити об’єм чи поверхню об’єктів природи та побуту, дослідити їх взаємне розташування та визначити оптимальні розміри. Дослідження геометричних тіл є первинним видом інтелектуальної діяльності людства. Геометрія вивчає просторові форми та їх відношення і тому використовується скрізь, де потрібна найменша точність у визначенні форми і розмірів. Встановлено, що кожний десятий винахід робиться із застосуванням геометрії за рахунок вибору зручної форми, вдалого розташування, тощо. Інженерам, архітекторам, будівельникам, дизайнерам, модельєрам, вченим, дослідникам у найрізноманітніших галузях науки необхідні ґрунтовні знання геометрії, зокрема знання про геометричні тіла.
Геометрія є одним із засобів інтелектуального розвитку людини, має велике розвиваюче значення, стимулює розвиток творчих здібностей. Цей предмет природно пов’язує можливості гармонійного розвитку образного та логічного мислення учнів. А курс стереометрії в рамках дедуктивної структури оперує уявленнями візуального просторового характеру. Просторові геометричні фігури є предметом вивчення стереометрії.
Розробкою змісту, форм і методів вивчення геометрії, зокрема стереометрії, займалися М. І. Антоненко, Г. П. Бевз, Н. В. Гібалова, Я. М. Жовнір та ін. Науково – методичне забезпечення процесу навчання геометрії розробляли Л. С. Атанасян, В. Г. Бевз, М. І. Бурда, Т. В. Гришина та ін. [].
Мета вивчення геометрії в 10 – 11-х класах – систематичне вивчення властивостей просторових геометричних фігур; розвиток просторових уявлень і уяви; засвоєння способів зображення просторових фігур на площині; обчислення площ поверхонь і об’ємів геометричних тіл і подальший розвиток логічного мислення.
У процесі вивчення стереометричного матеріалу систематизуються, узагальнюються і закріплюються геометричні знання, навички і вміння, одержані під час вивчення планіметрії в 7 – 9-х класах. Прикладна спрямованість вивчення матеріалу забезпечується широким використанням наочності, зверненням до життєвого досвіду учнів, розв’язуванням задач практичного змісту [8].
Організація самоосвітньої діяльності учнів під час опанування стереометрії.
Теоретична частина підготовки електронного підручника.
Дидактичні матеріали.
Стереометрія – частина геометрії, що вивчає властивості геометричних фігур у просторі.
АКСІОМИ СТЕРЕОМЕТРІЇ
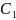 .
У просторі існує площина і (принаймні
одна) точка, що не лежить у цій площині.
.
У просторі існує площина і (принаймні
одна) точка, що не лежить у цій площині.
 .
Через будь-які три точки, що не лежать
на одній прямій, можна провести площину,
і до того ж тільки одну.
.
Через будь-які три точки, що не лежать
на одній прямій, можна провести площину,
і до того ж тільки одну.
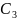 .
Якщо дві точки прямої лежать у площині,
то і вся пряма лежить у цій площині.
.
Якщо дві точки прямої лежать у площині,
то і вся пряма лежить у цій площині.
 .
Якщо дві площини мають спільну точку,
то вони перетинаються по прямій, яка
проходить через цю точку.
.
Якщо дві площини мають спільну точку,
то вони перетинаються по прямій, яка
проходить через цю точку.
Теорема. Через пряму і точку, що не лежить на ній, можна провести площину, і до того ж тільки одну.
Теорема. Через дві прямі, що перетинаються, можна провести площину, і до того ж тільки одну.
ПАРАЛЕЛЬНІСТЬ ПРЯМИХ І ПЛОЩИН
Мимобіжні і паралельні прямі
Означення. Дві прямі, які не лежать в одній площині, називають мимобіжними.
Теорема (ознака мимобіжних прямих). Якщо одна з двох прямих лежить у площині, а друга перетинає цю площину, але не перетинає першу пряму, то дані прямі мимобіжні.
Означення. Дві прямі називаються паралельними, якщо вони лежать в одній площині і не перетинаються.
Теорема. Через будь-яку точку простору, яка не лежить на даній прямій, можна провести пряму, паралельну даній, і тільки одну.
Теорема. Дві прямі, паралельні третій, паралельні.
Паралельність прямої і площини
Означення. Пряма і площина називаються паралельними, якщо вони не мають спільних точок.
Теорема (ознака паралельності прямої і площини). Якщо пряма, яка не лежить у площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині.
Паралельність площин
Означення. Дві площини називаються паралельними, якщо вони не мають спільних точок.
Теорема (ознака паралельності площин). Якщо дві прямі, які перетинаються і лежать в одній площині, паралельні двом прямим другої площини, то такі площини паралельні.
Теорема. Паралельні площини перетинаються січною площиною по паралельних прямих.
Теорема. Відрізки паралельних прямих, які відтинаються паралельними площинами, рівні.
Паралельне проектування і його властивості
Теорема. Якщо відрізки, які проектуються, не паралельні проектуючій прямій, то при паралельному проектуванні:
відрізки фігури зображаються відрізками;
паралельні відрізки – паралельними відрізками, або відрізками однієї прямої;
відношення довжин паралельних відрізків і відрізків однієї прямої зберігається.
ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ І ПЛОЩИН
Кут між прямими. Перпендикулярність прямих
Теорема. Якщо дві прямі, які перетинаються, паралельні іншим прямим, що перетинаються, то кут між першими прямими дорівнює куту між другими.
Означення. Кутом між мимобіжними прямими називають кут між прямими, які перетинаються і паралельні відповідно даним мимобіжним прямим.
Означення. Дві прямі називають перпендикулярними, якщо кут між ними дорівнює 90°.
Теорема. Якщо пряма перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої прямої.
Перпендикулярність прямої і площини
Означення. Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до будь-якої прямої, що лежить у площині і проходить через точку перетину.
Теорема (ознака перпендикулярності прямої і площини). Якщо пряма, яка перетинає площину, перпендикулярна до двох прямих цієї площини, що проходять через точку перетину, то вона перпендикулярна до площини.
Наслідки.
Пряма, перпендикулярна до двох прямих, що перетинаються, перпендикулярна до площини, яка проходить через ці прямі.
Пряма, перпендикулярна до площини, перпендикулярна до будь-якої прямої, що лежить у цій площині.
Якщо пряма перпендикулярна до двох сторін трикутника, то вона перпендикулярна і до третьої його сторони (рис.1).

Рис.1
Теорема. Якщо одна з двох паралельних прямих перпендикулярна до площини, то і друга пряма перпендикулярна до цієї площини.
Теорема. Дві прямі, перпендикулярні до однієї площини, паралельні.
Перпендикуляр і похила до площини
Означення. Перпендикуляром, опущеним з даної точки на дану площину, називають відрізок прямої, перпендикулярної до площини, що міститься між даною точкою і площиною.
Теорема (про три перпендикуляри). Пряма, проведена на площині перпендикулярно до проекції похилої, перпендикулярна до цієї похилої. І навпаки, якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
Теорема. Якщо з однієї точки, взятої поза площиною, проведені до цієї площини перпендикуляр і похилі, то:
дві похилі, які мають рівні проекції, рівні;
з двох похилих та більша, проекція якої більша;
перпендикуляр коротший за будь-яку похилу.
Перпендикулярні площини
Означення. Кутом між площинами, які перетинаються, називається кут між прямими, проведеними в цих площинах перпендикулярно до лінії їх перетину. Якщо площини паралельні, то вважають, що кут між ними дорівнює 0°.
Означення. Дві площини називаються перпендикулярними, якщо кут між ними дорівнює 90°.
Теорема (ознака перпендикулярності площин). Якщо одна з двох площин проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.
Теорема. Пряма, проведена в одній з двох перпендикулярних площин перпендикулярно до прямої їх перетину, перпендикулярна до другої площини.
Ортогональне проектування
Означення. Якщо проектуючи прямі перпендикулярні до площини проекцій, таке проектування називають ортогональним.
Теорема. Площа проекції многокутника на площину дорівнює площі даного многокутника, помноженій на косинус кута між їх площинами.
Теорема (просторова теорема Піфагора). Квадрат довжини будь-якого відрізка дорівнює сумі квадратів довжин його проекцій на три взаємно перпендикулярні прямі.
ВІДСТАНІ І КУТИ
Означення. Відстанню між двома фігурами називають відстань між найближчими точками цих фігур (якщо такі точки існують). Якщо дві фігури мають спільні точки, то вважають, що відстань між ними дорівнює 0.
Означення. Відстанню від точки до прямої називають перпендикуляр, опущений з точки на пряму, коротший від будь-якого відрізка, що сполучає цю точку з даною прямою.
Означення. Відстань від точки до відрізка не завжди дорівнює відстані від точки до прямої, якій належить цей відрізок. Вона може дорівнювати відстані від даної точки до кінця відрізка.
Означення. Відстань від точки до площини дорівнює довжині перпендикуляра, опущеного з даної точки на площину.
Означення. Відстанню між мимобіжними прямими називається довжина їхнього спільного перпендикуляра.
Означення. Відстань між паралельними площинами – довжина перпендикуляра, опущеного з будь-якої точки площини на паралельну їй площину.
Кут між прямою і площиною
Означення. Кутом між прямою і площиною називають кут між прямою і її проекцією на площину.
Теорема. Кут між похилою і площиною найменший з усіх кутів, які похила утворює з прямими, проведеними на площині через основу похилої.
Двогранні кути
Означення. Двогранним кутом називається фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує. Півплощини, які утворюють двогранний кут, називають гранями, а пряму, що їх обмежує, – ребром двогранного кута.
Означення. Лінійним кутом двогранного кута називається кут, утворений перетином даного двогранного кута площиною, перпендикулярною до його ребра.
ГЕОМЕТРИЧНЕ ТІЛО
Означення. Геометричне тіло являє собою частину простору, яку займає фізичне тіло.
Означення. Геометричною фігурою називається будь-яка множина точок площини або простору.
Означення. Точка називається граничною для фігури в просторі, якщо в будь-якій кулі з центром у цій точці знайдеться як точка даної фігури, так і точка, що не належить цій фігурі.
Означення. Множина граничних точок фігури називається її границею.
Означення. Точка фігури, яка не лежить на її границі, тобто не є її граничною точкою, називається внутрішньою точкою фігури.
Означення. Множина внутрішніх точок фігури називається її внутрішністю.
Означення. Про точки простору, які не лежать ні на границі, ні всередині фігури, говорять, що вони лежать зовні фігури або є її зовнішніми точками.
Означення. Фігура, що містить всі свої граничні точки (тобто свою границю), називається замкненою.
Означення. Тілом називається фігура в просторі, яка має дві властивості:
у неї є внутрішні точки, і будь-які дві з них можна з’єднати ламаною (або відрізком), що цілком проходить всередині фігури, тобто складається з внутрішніх точок;
фігура містить свою границю, та її границя співпадає з границею її внутрішності.
Означення. Границя тіла називається його поверхнею.
Означення. Фігура в просторі називається обмеженою, якщо її можна заключити в яку-небудь сферу.
Означення. Фігура називається опуклою, якщо разом з будь-якими двома своїми точками містить усі точки відрізка, що з’єднує їх.
Означення. Поверхня обмеженого опуклого тіла називається замкненою опуклою поверхнею.
Означення. Фігура називається простою, якщо вона обмежена і кожна пряма має скінчене число окремих точок і відрізків спільних з границею цієї фігури або не має таких точок і відрізків.
Поняття площі та об’єму
Означення. Дві фігури називають рівними, якщо їх можна сумістити за допомогою руху.
Означення. Площею простої плоскої фігури називається невід’ємна величина визначена для кожної простої плоскої фігури так, що:
рівні фігури мають рівні площі;
якщо плоска фігура складена зі скінченого числа простих плоских фігур, то її площа дорівнює сумі площ складових фігур;
одиницею вимірювання площ є площа квадрату, довжина ребра якого прийнята за одиницю вимірювання довжин.
Означення. Площею поверхні многогранника називається сума площ усіх його граней.
Означення. Об’ємом простої фігури називається невід’ємна величина, визначена для кожної простої фігури в просторі так, що:
рівні прості фігури мають рівні об’єми;
якщо проста фігура складена зі скінченого числа простих фігур, то її об’єм дорівнює сумі їх об’ємів;
одиницею вимірювання об’ємів є об’єм куба, довжина ребра якого прийнята за одиницю вимірювання довжин.
Означення. Два тіла, що мають рівні об’єми, називають рівновеликими.
МНОГОГРАННИКИ
Поняття многогранника
Означення. Многогранник – це обмежене тіло, поверхня якого складається зі скінченого числа плоских многокутників.
Означення. Многокутники, із яких складається поверхня многогранника, називаються його гранями. Сторони граней називаються ребрами, а вершини граней – вершинами многогранниками.
Означення. Відрізок, який з’єднує дві вершини, що не належать одній грані, називається діагоналлю многогранника.
Означення. Діагональною площиною многогранника називається площина, що містить діагональ многогранника.
Означення. Опуклим многогранником називається многогранник, який розташований з одного боку від площини кожної з граней.
Означення. Якщо поверхню многогранника розрізати по ребрах і розгорнути її так, щоб усі многокутники, які належать поверхні, лежали в одній площині, то отримаємо фігуру, яка називається розгорткою.
Теорема Ейлера. Якщо Г- число граней опуклого многогранника, Р – число ребер, В – число його вершин, то Г + В – Р = 2.
Правильні многогранники
Означення. Многогранник називається правильним, якщо всі його грані є рівними між собою правильними многокутниками і в кожній вершині многогранника сходиться одне і те ж число ребер.
Введемо
позначення: а
–
ребро многогранника, Г – кількість
граней,
 - кількість ребер (сторін) у кожної грані,
- кількість ребер (сторін) у кожної грані,
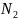 - кількість ребер у кожної вершини, В –
кількість вершин, Р – загальна кількість
ребер, S
– площа поверхні, V
– об’єм, R
– радіус описаної кулі, r
– радіус вписаної кулі.
- кількість ребер у кожної вершини, В –
кількість вершин, Р – загальна кількість
ребер, S
– площа поверхні, V
– об’єм, R
– радіус описаної кулі, r
– радіус вписаної кулі.
Назва многогранника |
Властивості многогранника та співвідношення між його елементами |
Тетраедр (правильний чотиригранник) |
Г
= 4,
|
Гексаедр (правильний шестигранник – куб) |
Г
= 6,
|
Октаедр (правильний восьмигранник) |
Г
= 8,
,
|
Додекаедр (правильний дванадцятигранник) |
Г
= 12,
|
Ікосаедр (правильний двадцятигранник) |
Г
= 20,
,
|
ПРИЗМА ТА ПАРАЛЕЛЕПІПЕД
Поняття призми та види призм
Означення. Призмою називається многогранник, у якого дві грані – рівні n-кутники, а решта n-граней – паралелограми.
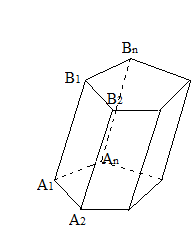
Рис.2
Означення.
Рівні
n-кутники
 ,
,
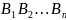 називаються
основами; паралелограми
називаються
основами; паралелограми
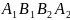 ,
,
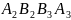 ,
… - бічними
гранями; а відрізки (
,
… - бічними
гранями; а відрізки ( ),
які сполучають відповідні вершини,
називаються бічними ребрами призми
(рис.2).
),
які сполучають відповідні вершини,
називаються бічними ребрами призми
(рис.2).
Означення. Призма, бічні ребра якої перпендикулярні площинам основ, називається прямою призмою.
Означення. Якщо бічні ребра призми не перпендикулярні площинам основ, то її називають похилою призмою.
Означення. Пряма призма, основою якої є правильний многокутник, називається правильною призмою.
Бічна поверхня призми
Означення. Перпендикулярним перерізом називається многокутник, який отримано при перерізі призми площиною, що перпендикулярна до кожного бічного ребра. Сторони цього многокутника перпендикулярні до ребер.
Теорема. Бічна поверхня призми дорівнює добутку периметра перпендикулярного перерізу на довжину бічного ребра.
Означення.
Площею
повної поверхні призми називається
сума площ її бічних граней (площа бічної
поверхні) і площ основ призми:
 .
.
Теорема. Об’єм прямокутного паралелепіпеда дорівнює добутку трьох його лінійних вимірів.
Теорема. Об’єм будь-якої призми дорівнює добутку площі її основи на висоту.
Поняття паралелепіпеда
Означення. Паралелепіпедом називається призма, основами якої є паралелограми.
Означення. Дві грані паралелепіпеда, що мають спільне ребро, називаються суміжними, а ті, що не мають спільного ребра – протилежними.
Означення. Дві вершини, що не належать одній грані, називаються протилежними.
Означення. Відрізок, що сполучає протилежні вершини, називається діагоналлю паралелепіпеда.
Означення. Якщо бічні ребра паралелепіпеда перпендикулярні до площини його основи, то паралелепіпед називається прямим.
Означення. Прямий паралелепіпед, основою якого є прямокутник, називається прямокутним паралелепіпедом.
Означення. Прямокутний паралелепіпед, у якого всі ребра рівні, називається кубом.
Властивості паралелепіпеда
Теорема. У паралелепіпеда:
протилежні грані рівні і паралельні;
усі чотири діагоналі перетинаються в одній точці і діляться в ній навпіл.
Теорема. У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох його лінійних вимірів.
ПІРАМІДА
Означення. Пірамідою називається многогранник, у якого одна грань, що називається основою, будь-який многокутник, а всі інші грані, які називаються бічними, - трикутники, що мають спільну вершину.
Многокутник
 є основою, а трикутники
є основою, а трикутники
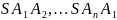 - бічними
гранями піраміди. Точка S
називається
вершиною піраміди, а відрізки
- бічними
гранями піраміди. Точка S
називається
вершиною піраміди, а відрізки
 - її
бічними ребрами (рис.3).
- її
бічними ребрами (рис.3).
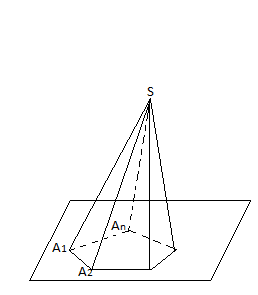
Рис.3
Означення. Піраміда називається n-кутною, якщо її основою є n-кутник.
Означення. Відрізок перпендикуляра, проведений з вершини піраміди до площини основи, називається висотою піраміди.
Означення. Переріз піраміди площиною, що проходить через два бічних ребра, які не лежать в одній грані, називається діагональним перерізом піраміди.
Означення. Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти співпадає з центром цього многокутника.
Означення. Віссю правильної піраміди називається пряма, яка містить її висоту.
Означення. Висота бічної грані правильної піраміди, яка проведена з її вершини, називається апофемою.
Означення. Зрізаною пірамідою називається частина піраміди, що знаходиться між основою і січною площиною, яка паралельна до основи (рис.4).
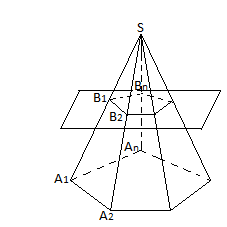
Рис.4
Означення. Відрізок перпендикуляра, проведений з будь-якої точки однієї основи до площини другої основи, називається висотою зрізаної піраміди.
Означення. Зрізана піраміда називається правильною, якщо вона отримана перерізом правильної піраміди площиною, яка паралельна до основи.
Властивості паралельних перерізів у піраміді
Теорема. Якщо піраміда перетинається площиною, яка паралельна до основи, то:
1)бічні ребра й висота діляться цією площиною на пропорційні частини;
2)при перерізі утворюється многокутник, подібний до основи;
3)площі перерізу і основи відносяться, як квадрати їх відстаней від вершини піраміди.
Теорема. Якщо дві піраміди з рівними висотами перетнути на однаковій відстані від вершини площинами, паралельними до основ, то площі перерізів пропорційні площам основ.
Поверхня піраміди
Означення. Сума площ бічних граней піраміди називається її бічною поверхнею.
Означення. Сума бічної поверхні піраміди і площі її основи називається повною поверхнею піраміди.
Теорема. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.
Теорема. Бічна поверхня правильної зрізаної піраміди дорівнює добутку півсум периметрів двох основ на висоту бічної грані (апофему).
Твердження. Дві піраміди з рівними площами основ і рівними висотами рівновеликі.
Теорема.
Об’єм
будь-якої піраміди дорівнює третині
добутку площі основи на висоту:
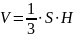 .
.
Теорема (обчислення об’єму піраміди через площі двох граней, двогранний кут та ребро):
Якщо
P
та
Q
– площі двох граней піраміди, а
–
довжина спільного ребра, β – величина
двогранного кута між цими гранями, то
об’єм піраміди можна обчислити за
формулою
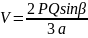 .
.
Теорема (обчислення об’єму піраміди через два протилежних ребра, відстань і кут між ними):
Якщо
a
та b
– довжини двох протилежних ребер
піраміди, d
– відстань, φ – кут між ними, то об’єм
піраміди можна знайти за формулою
 .
.
Теорема. Об’єм зрізаної піраміди дорівнює сумі об’ємів трьох пірамід, що мають висоту, яка дорівнює висоті зрізаної піраміди, й основами першої піраміди є нижня основа,другої – верхня основа заданої піраміди, а площа основи третьої піраміди дорівнює середньому геометричному площ верхньої та нижньої основ:
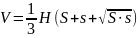 .
.
СИМЕТРІЯ МНОГОГРАННИКІВ
Центральна симетрія
Означення. Геометрична фігура F називається центральносиметричною, якщо існує точка О, відносно якої можна здійснити відображення кожної точки Х фігури F у таку точку Х' цієї самої фігури, яка розміщена на прямій ОХ на відстані ОХ', що дорівнює ОХ.
Властивості центральної симетрії
Означення. Фігура F', утворена з усіх точок, симетричних точкам фігури F відносно даної точки О, називається симетричною фігурі F відносно точки О.
Означення. Перетворення фігури F у фігуру F', при якому довільна точка Х фігури F переходить у симетричну відносно деякої точки О точку Х' фігури F', називається перетворенням симетрії відносно точки О.
Позначається
це перетворення через
 ,
причому, якщо точка Х' є образом точки
Х, то
(Х)
= Х'.
,
причому, якщо точка Х' є образом точки
Х, то
(Х)
= Х'.
З означення симетрії відносно деякої точки випливають такі властивості:
1.Для кожної точки О прямої, площини або простору існує центральна симетрія .
2.Для різних точок Х і Х' прямої, площини або простору існує така єдина симетрія , що (Х) = Х'. Центр симетрії - середина О відрізка ХХ'. Отже, центральна симетрія може бути задана або центром симетрії, або двома відповідними точками.
3.Центральна симетрія відображає фігуру F на фігуру F', причому різні точки першої фігури перетворюються в різні точки другої. Тому центральна симетрія є взаємно однозначним відображенням відносно її центра О.
4.Перетворення фігури F у фігуру F' називається рухом, якщо воно зберігає відстань між точками, тобто переводить будь-які дві точки X, Y фігури F у точки X', Y' фігури F' так, що XY = X'Y'. Отже, перетворення симетрії відносно точки є рух.
5.Точки, які лежать на прямій, переходять у результаті руху в точки, що також лежать на прямій, причому зберігається порядок їх взаємного розміщення.
6.Єдина нерухома точка перетворення симетрії відносно точки О – сама ця точка (центр симетрії). Нерухомою є також пряма, що проходить через центр симетрії, причому кожна точка прямої, що лежить по один бік від точки О, переходить у точку, що лежить по другий бік від точки О. Нерухомою є й кожна площина простору, що проходить через центр симетрії, причому нерухомою точкою такої площини є тільки центр симетрії.
7.Центральна симетрія на площині не змінює орієнтації трикутника.
8.Центральносиметричні трикутники, які не лежать в одній площині, мають протилежну орієнтацію.
Центральна симетрія многогранників
Теорема. Середина діагоналі паралелепіпеда є його центром симетрії.
Координатні формули симетрії відносно точки
Нехай
 і
і
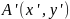 - дві взаємно симетричні точки відносно
точки
- дві взаємно симетричні точки відносно
точки
 .
Оскільки
.
Оскільки
 - середина відрізка
- середина відрізка
 ,
то її координати визначаються формулами:
,
то її координати визначаються формулами:
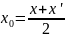 ,
,
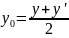 .
.
Записавши
ці рівності відносно
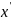 і
і
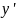 ,
дістанемо координатні формули симетрії
відносно точки:
,
дістанемо координатні формули симетрії
відносно точки:
 .
.
Симетрія відносно прямої та площини
Означення.
Нехай
l
– фіксована
пряма, Х – довільна точка. Проведемо
пряму
 ,
перпендикулярну до прямої l,
і від їх точки перетину
,
перпендикулярну до прямої l,
і від їх точки перетину
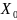 відкладемо відрізок
відкладемо відрізок
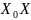 ',
що дорівнює відрізку
.
Побудована так точка
',
що дорівнює відрізку
.
Побудована так точка
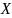 '
називається симетричною точці
відносно прямої l,
а перетворення фігури F
у фігуру F',
при якому кожна її точка
переходить у точку
',
симетричну відносно прямої l,
називається перетворенням симетрії
відносно прямої l.
Самі фігури F
і F'
називаються симетричними відносно
прямої l.
'
називається симетричною точці
відносно прямої l,
а перетворення фігури F
у фігуру F',
при якому кожна її точка
переходить у точку
',
симетричну відносно прямої l,
називається перетворенням симетрії
відносно прямої l.
Самі фігури F
і F'
називаються симетричними відносно
прямої l.
Означення. Якщо перетворення симетрії відносно прямої l переводить фігуру F саму у себе, то така фігура називається симетричною відносно прямої l, а пряма l називається віссю симетрії фігури F.
Перетворення
симетрії відносно прямої l
позначають символом
 ,
причому, якщо точка
'
фігури F'
є образом точки Х фігури F'
при симетрії
,
то це записують так:
(Х)
= Х'.
,
причому, якщо точка
'
фігури F'
є образом точки Х фігури F'
при симетрії
,
то це записують так:
(Х)
= Х'.
З означення симетричних точок, фігур і перетворення симетрії відносно прямої l площини випливають такі властивості:
1.Для кожної прямої l площини існує симетрія відносно цієї прямої.
2.Для різних точок Х, Х' площини існує така єдина симетрія , що (Х) = Х', (Х') = Х; пряма l перпендикулярна до відрізка ХХ' і проходить через його середину.
3.При перетворенні симетрії відносно прямої l кожна точка цієї прямої і сама пряма l переходять самі в себе, тобто залишаються нерухомими; переходять самі в себе і прямі, перпендикулярні до прямої l, причому півпряма кожної з них, що розташована по один бік від прямої l, переходить у півпряму, розміщену по другий бік від прямої l.
4.При перетворенні симетрії відносно прямої відрізок переходить у рівний йому відрізок, півпряма – у півпряму, пряма – в пряму, причому зберігається порядок взаємного розташування точок; кут переходить у рівний йому кут, одна з півплощин – у другу півплощину і навпаки.
5.Симетрія відносно прямої на площині змінює орієнтацію фігури.
Симетрію
відносно площини σ позначають
 ,
причому якщо точка А' є образом точки А
при такій симетрії, то записують:
(А)
= А'.
,
причому якщо точка А' є образом точки А
при такій симетрії, то записують:
(А)
= А'.
Основні властивості такої симетрії:
1.Точки, які лежать у площині симетрії σ, і тільки вони, нерухомі.
2.При симетрії відносно площини пряма перетворюється в пряму, причому пряма, яка лежить у площині симетрії, залишається нерухомою; пряма, перпендикулярна до площини симетрії, перетворюється в себе, причому одна півпряма переходить у другу і навпаки.
3.При симетрії відносно площини площина відображається в площину, причому якщо площина, перпендикулярна до площини симетрії, то вона відображається сама на себе.
4.При симетрії відносно площини тетраедр перетворюється в рівний тетраедр протилежної орієнтації.
Симетрія відносно прямої у просторі не змінює орієнтації фігури. Нерухомими елементами симетрії відносно прямої l у просторі є точки цієї прямої, прямі і площини, перпендикулярні до неї, і площини, які проходять через цю пряму.
Координатні формули симетрії відносно прямої й площини
Перетворення
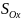 симетрії
відносно прямої
симетрії
відносно прямої
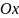 виражатиметься
такими формулами:
виражатиметься
такими формулами:
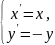 .
.
Поворот та його властивості
Означення. Поворотом навколо даної точки О на кут φ називається таке перетворення фігури F у фігуру F', при якому зберігається відстань між точками перетворюваної фігури і кожний промінь, що виходить з даної точки О, повертається на один і той самий кут в одному й тому самому напрямі. Точка повороту О називається центром повороту, а кут φ – кутом повороту.
Поворот
навколо точки О на кут φ позначають
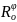 .
.
Властивості:
1.Поворот
на кут
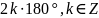 ,
є тотожним перетворенням.
,
є тотожним перетворенням.
2.Поворот
на кут
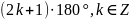 ,
навколо точки О є симетрією відносно
точки О.
,
навколо точки О є симетрією відносно
точки О.
3.Для кожної точки О площини існує перетворення повороту площини.
4.Для різних точок Х і Х' площини існує принаймні один поворот , такий, що (Х) = Х'.
5.При
повороті на кут
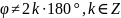 ,
нерухомою є тільки одна точка – центр
повороту.
,
нерухомою є тільки одна точка – центр
повороту.
6.При
повороті на кут
 нерухомих прямих немає.
нерухомих прямих немає.
7.При поворотах: відрізок перетворюється в рівний йому відрізок, півпряма – у півпряму, пряма – у пряму (причому зберігається порядок взаємного розташування їх точок), кут – у рівний йому кут; орієнтація будь-якої фігури і, зокрема, трикутника не змінюється: фігура перетворюється у рівну фігуру.
Фігури, що мають поворотну симетрію порядку n
Означення.
Якщо
фігура F
переходить
у себе при повороті навколо точки О (осі
l)
на
кут
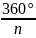 (n
– ціле
додатнє число), то говорять, що точка О
(вісь l)
для фігури F
є
центром (віссю) симетрії порядку n,
а фігура F
має
поворотну симетрію порядку n.
(n
– ціле
додатнє число), то говорять, що точка О
(вісь l)
для фігури F
є
центром (віссю) симетрії порядку n,
а фігура F
має
поворотну симетрію порядку n.
Означення.
Порядок
центра повороту або кількість самосуміщень
при повороті на 360° визначається формулою
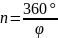 ,
де φ – кут найменшого повороту, при
якому фігури самосуміщаються. Якщо
фігура самосуміщається тільки при
повороті на кут 0° (або на кут
,
де φ – кут найменшого повороту, при
якому фігури самосуміщаються. Якщо
фігура самосуміщається тільки при
повороті на кут 0° (або на кут
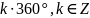 ),
180° (або
),
180° (або
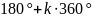 ),
120° (або
),
120° (або
 ),
то відповідний центр (вісь) називається
центром (віссю) повороту першого, другого
або третього порядку.
),
то відповідний центр (вісь) називається
центром (віссю) повороту першого, другого
або третього порядку.
Координатні формули повороту
 .
.
Паралельне перенесення
Означення.
Паралельним
перенесенням на площині xy
називається
таке геометричне перетворення, при
якому довільна її точка (x,y)
переходить у таку точку (x',y'),
що
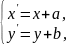 де
де
 і
і
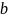 - деякі числа.
- деякі числа.
Паралельне перенесення в просторі визначається аналогічно і задається формулами:
 де
,
,
де
,
,
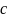 - деякі числа.
- деякі числа.
Властивості паралельного перенесення:
1)зберігає відстань між точками, тобто є рухом;
2)точки зміщує по паралельних (або таких, що збігаються) прямих на одну і ту саму відстань;
3)кожну пряму перетворює в паралельну пряму (або в себе);
4)не змінює орієнтації фігур;
5)півпряму, півплощину, кут перетворює відповідно в півпряму, півплощину, рівний кут; довільну фігуру – у фігуру, що їй дорівнює;
6)якщо
в системі
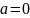 і
і
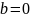 ,
то паралельне перенесення є тотожним
перетворенням площини.
,
то паралельне перенесення є тотожним
перетворенням площини.
ТІЛА ОБЕРТАННЯ
Циліндр
Означення. Круговим циліндром називається тіло, що складається з двох кругів, які не лежать в одній площині та суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів. Круги називаються основами циліндра, а відрізки, що сполучають точки кіл кругів, - твірними циліндра (рис.5).
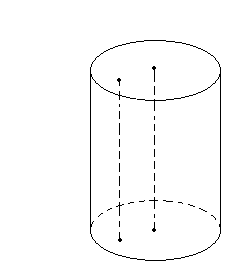
Рис.5
Означення. Перпендикуляр, опущений з будь-якої точки однієї основи на площину другої, називається висотою циліндра.
Означення. Пряма, що проходить через центри основ циліндра, називається віссю циліндра.
Означення. Якщо твірні циліндра перпендикулярні до площини основи, його називають прямим циліндром.
Теорема. Площина, паралельна площині основи циліндра, перетинає його бічну поверхню по колу, яке дорівнює колу основи.
Означення.
Площа
бічної поверхні циліндра дорівнює
добутку довжини кола основи на висоту
циліндра
 .
.
Означення. Дане тіло має об’єм V, якщо існують прості тіла, що містять його і що містяться в ньому, з об’ємами, які як завгодно мало відрізняються від V.
Означення.
Об’єм
циліндра дорівнює добутку площі основи
на висоту
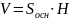 .
.
Вписана й описана призми
Означення. Призмою, вписаною у циліндр, називається така призма, у якої основи призми вписано в кола основ циліндра, а бічними ребрами є твірні циліндра (рис. 6).
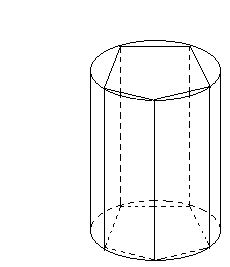
Рис.6
Означення. Дотичною площиною до циліндра називається площина, яка проходить через твірну циліндра і перпендикулярна до площини осьового перерізу, що містить цю твірну (рис. 7).
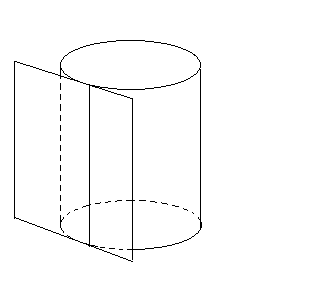
Рис.7
Означення. Призмою, описаною навколо циліндра, називається призма, у якої основи призми описано навколо основ циліндра, а бічні грані дотикаються до циліндра (рис. 8).
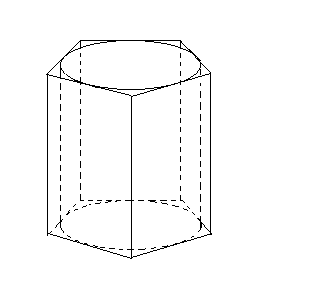
Рис.8
Конус
Означення. Круговим конусом називається тіло, яке складається з круга – основи конуса, точки, яка не лежить у площині цього круга – вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи (рис.9).
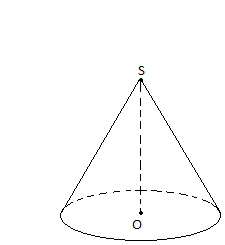
Рис.9
Означення. Відрізки, що сполучають вершину конуса з точками кола основи, називаються твірними конуса.
Означення. Конус називається прямим, якщо пряма, що сполучає вершину конуса з центром основи, перпендикулярна до площини основи.
Означення. Висотою конуса називається відрізок перпендикуляра, опущеного з вершини на площину основи.
Означення. Віссю прямого кругового конуса називається пряма, що містить його висоту.
Означення. Кожна площина, що проходить через вісь конуса, є площиною його симетрії.
Теорема (про переріз конуса).
Переріз конуса площиною, яка паралельна площині його основи, є круг подібний до круга основи конуса. Коефіцієнт подібності дорівнює відношенню відстані від вершини конуса до площини перерізу до висоти конуса.
Означення. Площина, яка паралельна основі конуса і перетинає конус, відтинає від нього менший конус. Частина, що залишилася, називається зрізаним конусом (рис.10).
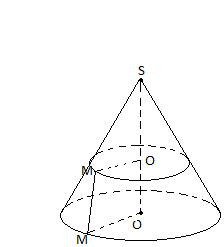
Рис.10
Означення. Висотою зрізаного конуса називається відрізок перпендикуляра, що опущений з довільної точки однієї з його основ на площину іншої.
Означення. Твірною зрізаного конуса є відрізок, що сполучає найближчі точки кіл основ.
Означення.
Площа
бічної поверхні конуса дорівнює добутку
половини довжини кола основи на твірну
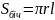 .
.
Означення. Об’єм конуса дорівнює третині добутку площі основи на висоту.
Вписана й описана піраміди
Означення. Пірамідою, вписаною в конус, називається така піраміда, основою якої є многокутник, вписаний у коло основи конуса, а вершиною – вершина конуса (рис. 11). Бічні ребра піраміди, вписаної у конус, є твірними конуса.
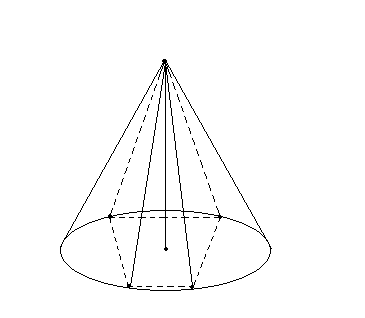
Рис.11
Означення. Дотичною площиною до конуса називається площина, яка проходить через твірну конуса і перпендикулярна до площини осьового перерізу, що містить цю твірну (рис. 12).
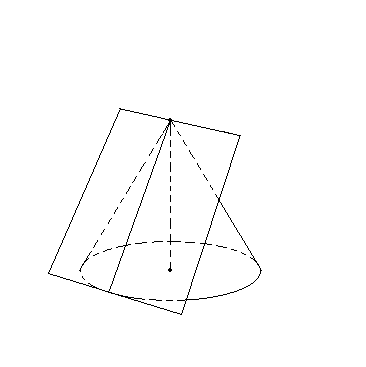
Рис.12
Означення. Пірамідою, описаною навколо конуса, називається піраміда, в основі якої лежить многокутник, описаний навколо основи конуса, а вершина співпадає з вершиною конуса (рис. 13). Площини бічних граней описаної піраміди є дотичними площинами до конуса.
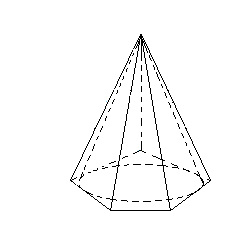
Рис.13
Куля і сфера
Означення. Кулею називається тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану (рис.14).
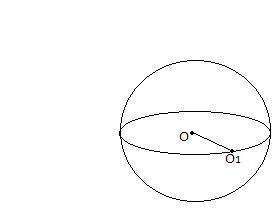
Рис.14
Означення. Межа кулі називається кульовою поверхнею або сферою.
Означення. Відрізок, що з’єднує центр кулі з точкою кульової поверхні, називається радіусом, а відрізок, що з’єднує дві точки кульової поверхні і проходить через центр кулі, називається діаметром кулі.
Означення. Площина, що проходить через діаметр кулі, називається діаметральною площиною.
Означення. Куля – це тіло, утворене обертанням півкруга навколо його діаметра як осі. Сфера утворюється внаслідок обертання півкола навколо діаметра.
Теорема. Діаметральна площина кулі є її площиною симетрії. Центр кулі є її центром симетрії.
Теорема. Будь-яка площина або не має спільних точок із сферою, або дотикається до неї, або перетинає її по колу. В останньому випадку коло має найбільший радіус, коли січна площина проходить через центр сфери.
Означення. Площина, яка має з кульовою поверхнею єдину спільну точку, називається дотичною площиною. Точка А називається точкою дотику (рис.15).
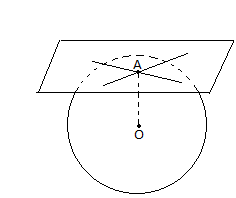
Рис.15
Теорема. Площина, дотична до кулі, перпендикулярна радіусу, проведеному в точку дотику.
Теорема. Лінія перетину двох сфер є коло.
Означення. Кульовим сегментом називається частина кулі, яку відтинає від неї січна площина.
Об’єм
кульового сегмента визначається:
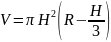 .
.
Площа
сегментної поверхні визначається: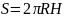 .
.
Означення. Кульовим сектором називається тіло, яке утворюється з кульового сегмента і конуса таким чином. Якщо кульовий сегмент менший за півкулю, то кульовий сегмент доповнюється конусом, у якого вершина знаходиться в центрі кулі, а основою є основа сегмента. Якщо ж сегмент більший від півкулі, то вказаний конус із нього вилучається (рис.16).
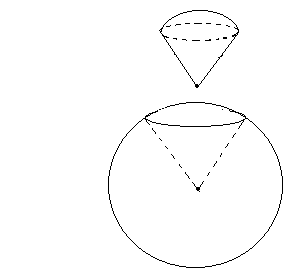
Рис.16
Об’єм
кульового сектора визначається:
 ,
де
R
–
радіус кулі, H
– висота відповідного кульового
сегмента.
,
де
R
–
радіус кулі, H
– висота відповідного кульового
сегмента.
Площа повної поверхні кульового сектора визначається:
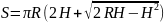 .
.
Означення. Кульовим шаром називається частина кулі, що міститься між двома паралельними площинами перерізу. Круги, що утворяться в перерізі кулі цими площинами, називаються основами кульового шару, а відстань між площинами – висотою кульового шару.
Об’єм
кульового шару визначається:
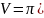 ,
де
,
де
 - радіус кулі,
- радіус кулі,
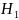 і
і
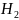 - висоти кульових сегментів.
- висоти кульових сегментів.
Площа кульового шару визначається: .
Об’єм
кулі визначається:
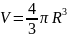 .
.
Вписані й описані многогранники
Означення. Многогранник називається вписаним у кулю, якщо всі його вершини лежать на сфері. Ця сфера називається описаною навколо цього многогранника.
Означення. Многогранник називається описаним навколо кулі, якщо всі його грані дотикаються до поверхні кулі – сфери. Ця сфера називається вписаною в даний многогранник.
Твердження. Центр кулі, описаної навколо правильної піраміди, лежить на її осі.
Теорема (про сферу, описану навколо трикутної піраміди).
Трикутна піраміда має єдину описану сферу.
Теорема (про сферу, вписану в піраміду).
У будь-якої трикутної піраміди існує єдина вписана сфера.
Примітка. Будь-який конус також має описану й вписану сферу. Циліндр завжди має описану сферу. Але вписати сферу можна не в довільний циліндр, а лише в циліндр із квадратним осьовим перерізом.
Тест №1
1.Дано
куб
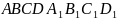 .
Укажіть точку, яка належить площині
(
.
Укажіть точку, яка належить площині
(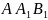 ).
).
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
Відповідь: 4.
2.У просторі дано точку А і пряму b. Скільки існує різних прямих, які проходять через точку А і НЕ ПЕРЕТИНАЮТЬ пряму b?
1 |
2 |
3 |
4 |
5 |
Жодної |
Одна |
Безліч |
Одна або безліч |
Жодної або безліч |
Відповідь: 5.
3.Скільки прямих перетину можуть мати три різні площини α, β і γ?
1 |
2 |
3 |
4 |
5 |
Або одну, або жодною |
Або три, або жодної |
Або три, або одну |
Або три , або одну, або жодної |
Інша відповідь |
Відповідь: 1.
4.З точки А до площини π проведено дві похилі AB = 30 і AC = 40. Знайдіть відстань від точки А до площини π, якщо довжини проекцій цих похилих відносяться як 9:16.
Відповідь: 24.
5.У правильному многограннику 12 ребер і 8 вершин. Скільки в ньому граней?
1 |
2 |
3 |
4 |
5 |
4 |
6 |
8 |
10 |
12 |
Відповідь: 2.
6.Яку найменшу кількість граней може мати піраміда?
1 |
2 |
3 |
4 |
5 |
3 |
4 |
5 |
6 |
9 |
Відповідь: 2.
7.Укажіть НЕПРАВИЛЬНЕ твердження.
А |
Протилежні грані будь-якого паралелепіпеда мають однакові площі |
Б |
Усі діагоналі будь-якого прямокутного паралелепіпеда мають однакову довжину |
В |
Діагоналі бічних граней будь-якої прямої трикутної призми рівні між собою |
Г |
Довжини бічних ребер будь-якої прямої трикутної призми дорівнюють її висоті |
Д |
Площі основ будь-якої шестикутної призми рівні між собою |
Відповідь: В.
8.Із n однакових маленьких кубиків склали великий куб. Укажіть число, яке може бути значенням n.
1 |
2 |
3 |
4 |
5 |
16 |
27 |
30 |
45 |
54 |
Відповідь: 2.
9.Установіть відповідність між рисунками (1-4), на яких зображені розгортки многогранників, і цими многогранниками (А-Д).
![]() А.
Трикутна піраміда
А.
Трикутна піраміда
![]() Б.
Трикутна призма
Б.
Трикутна призма
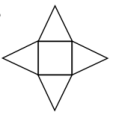 В.
Чотирикутна піраміда
В.
Чотирикутна піраміда
![]() Г.
Чотирикутна призма
Г.
Чотирикутна призма
Д. Шестикутна піраміда
Відповідь: 1 – Б; 2 – А; 3 – В; 4 – Г.
10.У піраміді MPQS (M - вершина піраміди) ребро MQ є висотою, PQ=15, QS=13, PS=4. Знайдіть об’єм піраміди, якщо відстань від точки M до ребра дорівнює 37.
Відповідь: 280.
11.Які геометричні фігури НЕ МОЖНА отримати як перерізи циліндра?
1 |
2 |
3 |
4 |
5 |
Трикутник |
Чотирикутник |
Круг |
Еліпс |
Усі наведені фігури не можна отримати |
Відповідь: 1.
12.Які геометричні фігури НЕ МОЖНА отримати як перерізи конуса?
1 |
2 |
3 |
4 |
5 |
Трикутник |
Чотирикутник |
Круг |
Еліпс |
Усі наведені фігури не можна отримати |
Відповідь: 2.
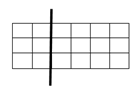
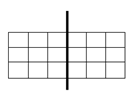
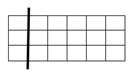
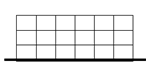
13.Прямокутники, зображені на рисунках, обертають навколо виділених осей. Укажіть рисунок, який відповідає тілу обертання з НАЙМЕНШОЮ площею бічної поверхні.
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
Відповідь: 2.
14.Прямокутний трикутник, гіпотенуза якого дорівнює 6 см, а один із гострих кутів дорівнює 30°, обертається навколо більшого катета. Знайдіть висоту конуса, утвореного внаслідок цього обертання.
1 |
2 |
3 |
4 |
5 |
|
3 см |
|
6 см |
12 см |
Відповідь: 3.
15.Виразіть об’єм циліндра V через радіус його основи R, якщо висота цього циліндра вдвічі більша за радіус його основи.
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
Відповідь: 4.
16.Круг, площа якого дорівнює а, обертається навколо свого діаметра. Знайдіть площу сфери, яка обмежує кулю, утворену внаслідок цього обертання.
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
Відповідь: 5.
17.Уявіть, що у вас є 5 видів фужерів: А, Б, В, Г, Д, кожний із яких має форму конуса з радіусом основи R та висотою h. Укажіть вид фужерів, які потрібно поставити на святковий стіл, якщо ви прагнете, наповнивши їх ущерть, налити в них ЯКНАЙБІЛЬШЕ рідини.
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
Відповідь: 1.
18.У циліндр вписано правильну трикутну призму, а в призму – інший циліндр. Знайдіть відношення об’єму меншого циліндра до об’єму більшого циліндра.
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
Відповідь: 2.
19.Установіть відповідність між плоскими фігурами (1-4) і тілами (А-Д), які утворені внаслідок обертання цих плоских фігур навколо прямих, що зображені пунктиром.

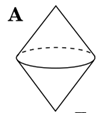
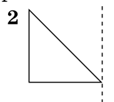

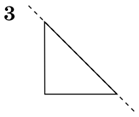
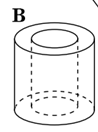
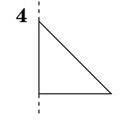
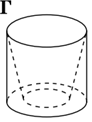
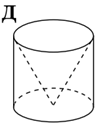
Відповідь: 1 – Г; 2 – Д; 3 – А; 4 – Б.
20.На рисунку зображено розгортку поверхні многогранника, яка складається з двох квадратів і чотирьох однакових прямокутників. Довжини суміжних сторін прямокутників дорівнюють 4 і 9 . Знайдіть площу повної поверхні цього многогранника.
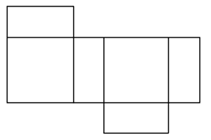
Відповідь: 306.
Тест №2
1.На
малюнку зображено прямокутний
паралелепіпед. Яке взаємне розташування
прямих
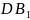 і
і
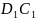 ?
?
1 |
2 |
3 |
4 |
5 |
Перетинаються |
Мимобіжні |
Паралельні |
Визначити неможливо |
Перпендикулярні |
Відповідь: 2.
2.Якщо дві суміжні сторони трапеції паралельні площині іншої трапеції, то площини цих трапецій…
1 |
2 |
3 |
4 |
5 |
Співпадають |
Паралельні |
Паралельні або співпадають |
Перпендикулярні |
Можуть бути розташовані як завгодно |
Відповідь: 2.
3.Якщо одна з двох площин перпендикулярна прямій, а інша площина паралельна цій прямій, то ці площини…
1 |
2 |
3 |
4 |
5 |
Перпендикулярні |
Співпадають |
Паралельні |
Паралельні або співпадають |
Інша відповідь |
Відповідь: 1.
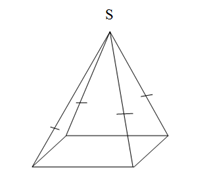
4.Точка S, яка не лежить в площині прямокутника з діагоналлю 10 см, віддалена від кожної з його вершин на 6 см. Відстань від точки S до площини прямокутника дорівнює…
1 |
2 |
3 |
4 |
5 |
|
|
|
|
Інша відповідь |
Відповідь: 2.
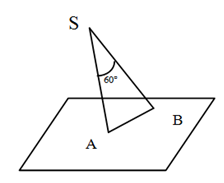
5.З точки S, яка знаходиться на відстані а від площини, проведені дві похилі, які утворюють з площиною кути в 45°, а між собою - в 60°. Відстань між кінцями похилих дорівнює…
1 |
2 |
3 |
4 |
5 |
см |
см |
см |
см |
Інша відповідь |
Відповідь: 3.
6.Величина двугранного кута при бічному ребрі правильної п’ятикутної призми дорівнює…
1 |
2 |
3 |
4 |
5 |
216° |
72° |
108° |
Величині, яка відмінна від наведених |
156° |
Відповідь: 3.
7.Перетином правильної трикутної призми не може бути…
1 |
2 |
3 |
4 |
5 |
Правильний трикутник |
Трапеція |
Прямокутник |
Шестикутник |
Інша відповідь |
Відповідь: 4.
8.В скільки разів треба збільшити ребра прямокутного паралелепіпеда, щоб його об’єм збільшився в два рази?
1 |
2 |
3 |
4 |
5 |
В 8 |
В 2 |
В
|
В
|
Інша відповідь |
Відповідь: 4.
9.Кут між висотою й апофемою правильної чотирикутної піраміди, в якій висота вдвічі коротша сторони основи, дорівнює…
1 |
2 |
3 |
4 |
5 |
60° |
90° |
45° |
30° |
Інша відповідь |
Відповідь: 3.
10.Площа перетину кулі радіуса 5 см площиною, яка знаходиться на відстані 4 см від центру, дорівнює…
1 |
2 |
3 |
4 |
5 |
|
|
|
|
Інша відповідь |
Відповідь: 2.
11.Обчисліть об’єм піраміди, основою якої є ромб із діагоналями 5 і 12, а висота цієї піраміди дорівнює 14.
Відповідь: 20.
12.Точка лежить на площині, яка дотикається до кулі радіуса 1 см, на відстані 1 см від точки дотику. Відстань від цієї точки до центру кулі дорівнює…
1 |
2 |
3 |
4 |
5 |
см |
1 см |
|
|
2 см |
Відповідь: 1.
13.Діаметр основи прямого кругового циліндра дорівнює 2 м. Деяка площина віддалена від осьового перетину прямого кругового циліндра на відстань 1,5 м і паралельна йому. Як розташовані циліндр і площина?
1 |
2 |
3 |
4 |
5 |
Не мають спільних точок |
Мають одну спільну точку |
Перетинаються по кругу |
Перетинаються по прямокутнику |
Інша відповідь |
Відповідь: 1.
14.Осьовим
перетином циліндра є квадрат, діагональ
якого дорівнює
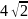 см. Об’єм циліндра дорівнює…
см. Об’єм циліндра дорівнює…
1 |
2 |
3 |
4 |
5 |
|
|
|
|
Інша відповідь |
Відповідь: 3.
15.Висота прямого кругового конуса дорівнює діаметру основи. Відношення площі його основи до площі бічної поверхні дорівнює…
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
Відповідь: 2.
16.Два
кола
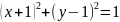 і
і
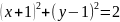 …
…
1 |
2 |
3 |
4 |
5 |
Перетинаються |
Дотикаються |
Не мають спільних точок |
Співпадають |
Інша відповідь |
Відповідь: 3.
17.Точка
К
рівновіддалена від усіх вершин трикутника
зі сторонами 5 см, 12 см і 13 см і знаходиться
на відстані
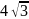 см від площини цього трикутника. Знайдіть
відстань від точки К
до кожної з вершин даного трикутника.
см від площини цього трикутника. Знайдіть
відстань від точки К
до кожної з вершин даного трикутника.
Відповідь: 9,5.
18.У правильній зрізаній чотирикутній піраміді діагоналі більшої та меншої основ дорівнюють 3 см і 1 см відповідно, а двогранні кути при меншій основі дорівнюють 120°. Знайдіть площу бічної поверхні цієї зрізаної піраміди.
Відповідь: 8.
19.З паперу вирізано круговий сектор радіуса 18 з центральним кутом 240°. З цього сектора без перекриттів згорнуто конус. Знайдіть радіус основи цього конуса.
Відповідь: 12.
20.У
правильну чотирикутну призму з висотою
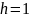 і стороною
і стороною
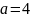 вписано циліндр. У цей циліндр вписано
правильну чотирикутну призму, в яку
знову вписано циліндр, і т.д. Знайдіть
суму об’ємів усіх призм, які при цьому
утворилися.
вписано циліндр. У цей циліндр вписано
правильну чотирикутну призму, в яку
знову вписано циліндр, і т.д. Знайдіть
суму об’ємів усіх призм, які при цьому
утворилися.
Відповідь: 32.
Тест №3
1.Скільки існує площин, які паралельні даній прямій і які проходять через дану точку?
А |
Б |
В |
Г |
Д |
Нескінченно багато або жодної |
Жодної |
Нескінченно багато |
Одна або жодної |
Одна |
Підказка
Зверніть увагу на те, що відповідь не залежить від взаємного розташування даних прямої та точки
Розв’язок
1 випадок 2 випадок
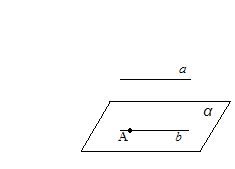

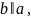 точка
точка
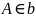
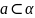

Відповідь: В.
2.Пряма а лежить у площині β, а пряма m паралельна прямій а та має спільну точку з площиною β. Яке взаємне розташування прямої m та площини β?
А |
Б |
В |
Г |
Д |
Пряма m лежить у площині β |
Пряма m і площина β перетинаються |
Пряма m паралельна площині β |
Можуть бути розташовані як завгодно |
Інша відповідь |
Підказка
Скористайтеся тим, що паралельні прямі a і m визначають площину
Розв’язок
Якщо пряма має спільну точку з площиною, то вона або перетинає її, або належить їй. Так як пряма має спільну точку з площиною і є паралельною прямій, яка належить площині, то ця пряма теж належить площині.
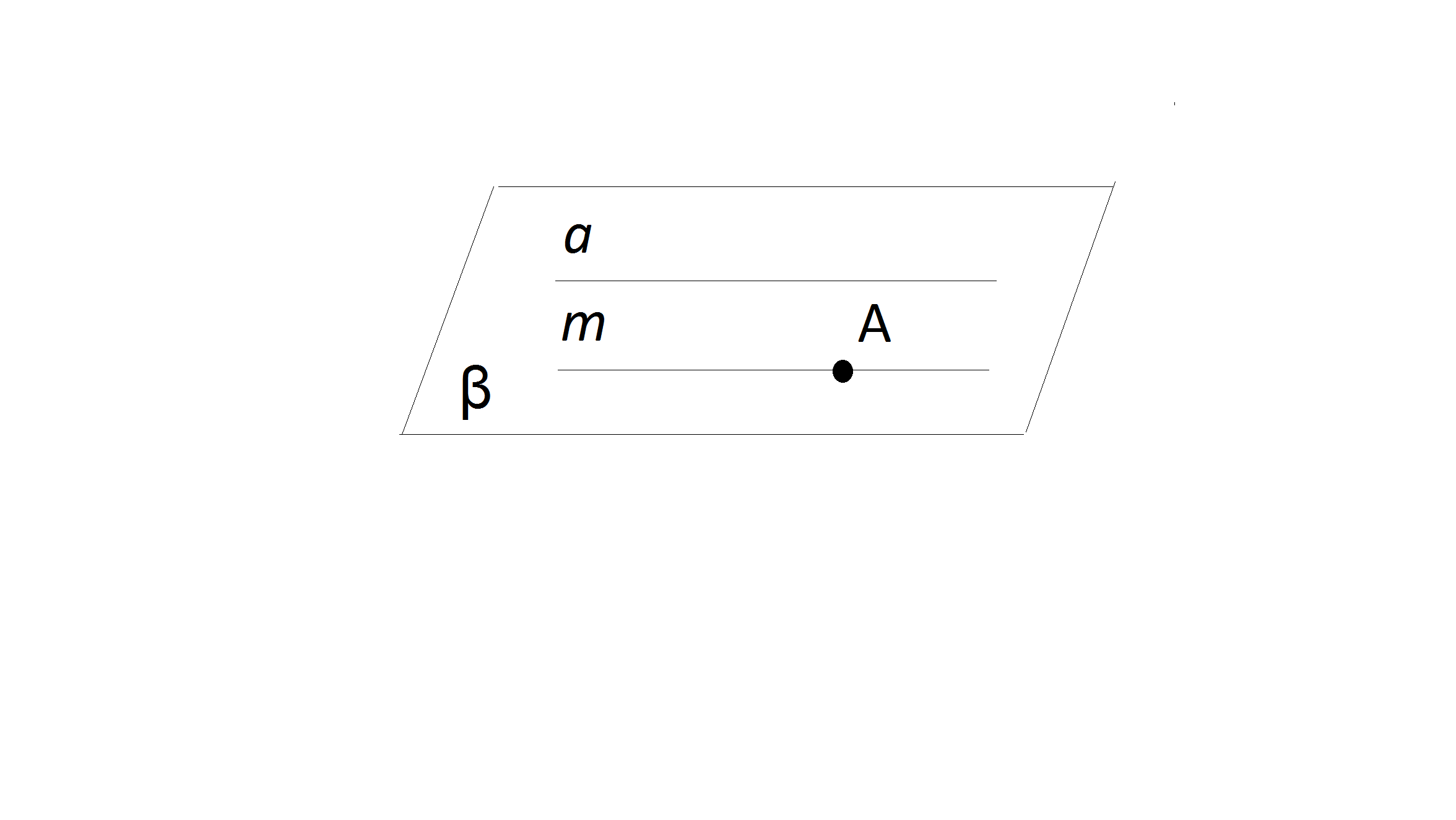
Відповідь: А.
3.Скільки площин проходять через дану точку простору перпендикулярно до даної прямої?
А |
Б |
В |
Г |
Д |
Жодної |
Одна |
Нескінченно багато |
Відповідь залежить від розташування точки |
Інша відповідь |
Підказка
Зверніть увагу на те, що відповідь не залежить від взаємного розташування даної точки та даної прямої
Розв’язок
1 випадок 2 випадок


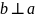 Точка
Точка
Відповідь: Б.
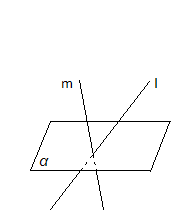
4.Скільки площин, які перпендикулярні даній площині, проходять через пряму, яка не є перпендикулярною до даної площини?
А |
Б |
В |
Г |
Д |
Нескінченно багато |
Жодної |
Одна |
Дві |
Одна або жодної |
Підказка
Зверніть увагу на те, що площина, яка перпендикулярна до даної площини і яка проходить через пряму l, яка не перпендикулярна до даної площини, проходить через пряму m, яка перпендикулярна площині α і яка проходить через точку перетину даної прямої l та даної площини α
Розв’язок
Площина β, яка проходить через пряму l, що не є перпендикулярною до даної площини α,також проходить через пряму m, перпендикулярною до площини α і проходить через точку перетину прямої l і площини α, то така площина – єдина.

Відповідь: В.
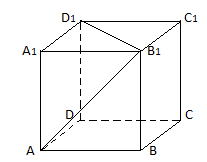
5.Дано
куб
.
Чому дорівнює кут між прямими
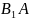 та
та
 ?
?
А |
Б |
В |
Г |
Д |
90° |
60° |
45° |
30° |
15° |
Підказка
Зверніть
увагу на вид трикутника
Розв’язок
Квадрат
 дорівнює
квадрату
дорівнює
квадрату
 й
дорівнює квадрату
й
дорівнює квадрату
 ,
так як
куб.
,
так як
куб.
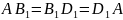 - діагоналі квадратів. Отже трикутник
- діагоналі квадратів. Отже трикутник
рівносторонній.
 .
.
Відповідь: Б.
6.Точка S, яка не лежить в площині прямокутника з діагоналлю 10 см віддалена від кожної з його вершин на 6 см. Відстань від точки S до площини прямокутника дорівнює…
А |
Б |
В |
Г |
Д |
8 см |
см |
см |
4 см |
12 см |
Підказка
Визначте розташування ортогональної проекції точки S на площину прямокутника, використовуючи те, що проекція точки S співпадає з центром кола, описаного навколо прямокутника
Розв’язок
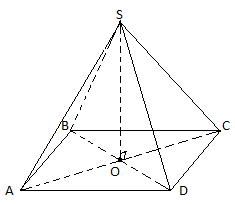
Трикутник
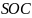 – прямокутний, так як
– прямокутний, так як
 – висота.
– висота.
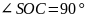 .
За теоремою Піфагора:
.
За теоремою Піфагора:
 ;
;
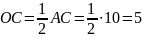 см
см
 см
см
 см.
см.
Відповідь: Б.
7.Об’єм
правильної трикутної призми дорівнює
8
 ,
висота основи – 2 см. Площа бічною
поверхні призми дорівнює…
,
висота основи – 2 см. Площа бічною
поверхні призми дорівнює…
А |
Б |
В |
Г |
Д |
6
|
12 |
36 |
24 |
Інша відповідь |
Підказка
Скористайтеся тим, що добуток сторони основи призми на її висоту використовується для обчислення і об’єму прямої призми і площі її бічної поверхні
Розв’язок

;
 ;
;
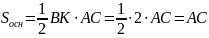 од.кв.
од.кв.
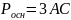 ;
;
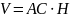 ;
;
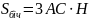 ;
;
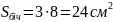 .
.
Відповідь: Г.
8.Перетином правильної трикутної призми не може бути…
А |
Б |
В |
Г |
Д |
Правильний трикутник |
Трапеція |
Прямокутник |
Шестикутник |
Інша відповідь |
Підказка
Зверніть увагу на те, що у трикутної призми п’ять граней
Розв’язок
Перетином однієї площини з п’ятьма гранями трикутної призми не може бути шестикутник
Відповідь: Г.
9.Діагональ куба дорівнює 6 см. Чому дорівнює ребро цього куба?
А |
Б |
В |
Г |
Д |
|
|
см |
2 см |
11 см |
Підказка
Скористайтеся просторовою теоремою Піфагора
Розв’язок

Скористаємось
формулою:
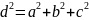
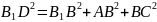
Так
як
– куб, то

 ;
;
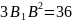 ;
;
 ;
;
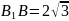 см.
см.
Відповідь: А.
10.Як зміниться об’єм правильної піраміди, якщо її висоту збільшити в 3 рази, а сторону основи зменшити в 3 рази?
А |
Б |
В |
Г |
Д |
Збільшиться в 3 рази |
Не зміниться |
Зменшиться в 3 рази |
Зменшиться в 9 разів |
Збільшиться в 9 разів |
Підказка
Використайте
те, що при зменшенні (збільшенні) сторін
правильного многокутника в k
разів
отримаємо правильний многокутник,
подібний даному, з коефіцієнтом подібності
к. тому площа його в
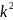 разів менше (більше) площі вихідного
многокутника
разів менше (більше) площі вихідного
многокутника
Розв’язок
 ;
;
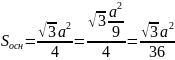 ;
;
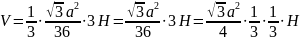 ;
;
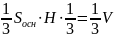
Відповідь: В.
11.Вершина трикутної піраміди, основою якої є прямокутний трикутник з катетами 1 см і 2 см, віддалена від вершин основи на 1,5 см. Чому дорівнює висота піраміди?
А |
Б |
В |
Г |
Д |
|
1 см |
|
|
5 см |
Підказка
Зверніть увагу на те, що ортогональною проекцією вершини даної піраміди є центр кола, яке описане навколо основи
Розв’язок
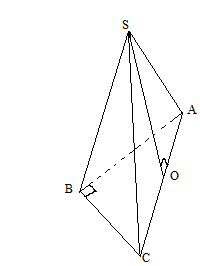
SB = SC = SA = 1,5 см, основою висоти є центр кола, описаного навколо трикутника. Трикутник АВС – прямокутний, центр описаного кола лежить на середині гіпотенузи.
З
 :
:
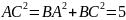 ;
;
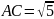 ;
;
 .
.
З
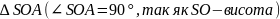 :
:
 .
.
Відповідь: Б.
12.Через середини ребер SA і SC правильного тетраедра SABC проведена площина, яка паралельна ребру BS. В перетині отримали…
А |
Б |
В |
Г |
Д |
Правильний трикутник |
Ромб |
Рівнобедрений трикутник |
Рівнобічна трапеція |
Інша відповідь |
Підказка
Скористайтеся тим, що шукана площина проходить паралельно одному з бічних ребер, тому дві сторони перерізу вже паралельні
Розв’язок

Так як SABC – правильний тетраедр, то KN = LM як середні ліній рівних трикутників SAC та АВС. Аналогічно NM = KL. Звідси випливає, що KN = LM = NM = KL як середні лінії рівних трикутників ⇒ KLMN – ромб.
Відповідь: Б.
13.Діаметри двох куль 25 і 29 см, а відстань між їх центрами дорівнює 36 см. Ці кулі…
А |
Б |
В |
Г |
Д |
Дотикаються |
Не мають спільних точок |
Перетинаються |
Довільно розташовані |
Інша відповідь |
Підказка
Порівняйте відстань між центрами куль і суму їх радіусів
Розв’язок
Радіус першої кулі дорівнює 12,5 см, а радіус другої кулі дорівнює 14,5. Якщо б кулі дотикались, то відстань між їх центрами дорівнювала 12,5 + 14,5 = 27 см. Але, так як відстань між центрами двох куль дорівнює 36 см, то ці кулі не мають спільних точок.
Відповідь: Б.
14.В скільки разів збільшиться об’єм кулі, якщо його радіус збільшити в 2 рази?
А |
Б |
В |
Г |
Д |
В 2 |
В 4 |
В 8 |
В 16 |
В 32 |
Підказка
Скористайтеся формулою для обчислення об’єму кулі
Розв’язок
Об’єм кулі дорівнює:
Збільшимо в 2 рази радіус та отримаємо:
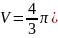
Відповідь: В.
15.Осьовим перерізом циліндра є квадрат, діагональ якого дорівнює см. Чому дорівнює об’єм циліндра?
А |
Б |
В |
Г |
Д |
|
|
|
|
Інша відповідь |
Підказка
Зверніть увагу на те, що сторонами осьового перетину циліндра є діаметр основи й твірна циліндра, довжина якої дорівнює висоті циліндра
Розв’язок

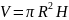 ;
;
 ;
;
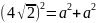 ;
;
 ;
;
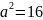 ;
;
;
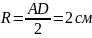 ;
;
 .
.
Відповідь: В.
16.В скільки разів треба зменшити радіус основи прямого кругового циліндра, не змінюючи його висоти, щоб його об’єм зменшився втричі?
А |
Б |
В |
Г |
Д |
В 3 рази |
В 9 разів |
В
|
В
|
В 2 рази |
Підказка
Скористайтеся тим, що в формулу для обчислення об’єму циліндра радіус його основи входить в другому степеню
Розв’язок
;
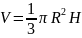 ;
;
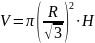
Таким чином радіус основи прямого кругового циліндра треба зменшити у разів.
Відповідь: В.
17.Осьовим перерізом конуса є прямокутний трикутник. Радіус основи конуса дорівнює 6 см. Чому дорівнює площа осьового перетину конуса?
А |
Б |
В |
Г |
Д |
9 |
12 |
18 |
36 |
Інша відповідь |
Підказка
Скористайтеся тим, що осьовим перетином конуса є рівнобедрений прямокутний трикутник
Розв’язок
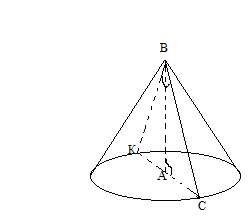
Розглянемо переріз конуса:

З
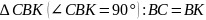 – як
твірні конуса, отже трикутник
– як
твірні конуса, отже трикутник
 – рівнобедрений.
– рівнобедрений.
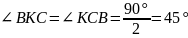 .
ВА
– висота трикутника СВК. Так як трикутник
СВК рівнобедрений, вона також є медіаною.
Отже СК = СА+АК = 12.
За
теоремою Піфагора з трикутника СВК:
.
ВА
– висота трикутника СВК. Так як трикутник
СВК рівнобедрений, вона також є медіаною.
Отже СК = СА+АК = 12.
За
теоремою Піфагора з трикутника СВК:
 ;
;
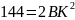 ;
;
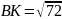 .
.
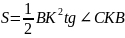 ;
;
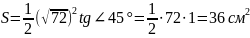 .
.
Відповідь: Г.
18.Твірна
прямого кругового конуса дорівнює 6 см,
площа його бічної поверхні дорівнює
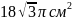 .
Чому дорівнює висота конуса?
.
Чому дорівнює висота конуса?
А |
Б |
В |
Г |
Д |
см |
см |
|
см |
1 см |
Підказка
Спочатку знайдіть радіус основи конуса
Розв’язок

 ;
;
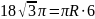 ;
;
 см.
см.
С
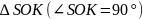 :
:
 ;
;
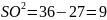 ;
;
 см.
см.
Відповідь: В.
19.Радіус
основи прямого кругового конуса дорівнює
2 см, а його об’єм дорівнює
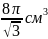 . Твірна конуса нахилена до площини
основи під кутом…
. Твірна конуса нахилена до площини
основи під кутом…

А |
Б |
В |
Г |
Д |
|
|
|
|
Інша відповідь |
Підказка
Спочатку знайдіть висоту конуса
Розв’язок

 ;
;
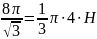 ;
;
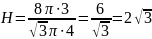 ;
;
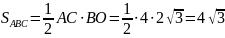 ;
;

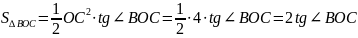
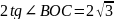
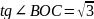
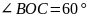 .
.
Відповідь: В.
20.Куча каміння має форму прямого кругового конуса з довжиною кола основи 18 м й твірною 5 м. Об’єм кучі каміння приблизно дорівнює… (оберіть найбільш точний результат)
А |
Б |
В |
Г |
Д |
20
|
35 |
70 |
55 |
Інша відповідь |
Підказка
Скористайтеся формулою для обчислення об’єму прямого кругового конуса:
,
де
– радіус основи,
 – висота конуса
– висота конуса
Розв’язок
;
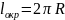 ;
;
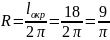 ;
;
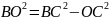 ;
;
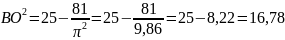 ;
;
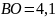
 .
.
Відповідь: Б.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
Буряк В.К. Формування у школярів потреби в самоосвіті // Рідна школа, 2000, №9, с.55-57.
Громцева А.К. Формирование у школьников готовности к самообразованию: Учеб. пособие по спецкурсу для студ. пед. ин-тов. М.: Просвещение, 1983. - 144 с.
Громцева А.К., Карпова А.Ф. и др. Руководство самообразованием школьников. – М.: Просвещение, 1983.
Кулюткин Ю.Н. Исследование познавательной деятельности учащихся вечерней школы. — М.: Педагогика, 1977. -152 с.
Матюшкин А.М. Развитие творческой активности школьников. - М.: Педагогика, 1991. - 160.
Сериков Г.Н. Обучение как условие самоподготовки к профессиональной деятельности. - Иркутск: Изд. Иркут. ун-та, 1985. -36 с.
http://subject.com.ua/psychology/pedagog_psychology/38.html
Програма для загальноосвітніх навчальних закладів математика 5-11 класи.

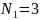 ,
,
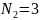 ,
В = 4, Р = 6;
,
В = 4, Р = 6;

 ,
,
В = 8,
Р = 12;
,
,
В = 8,
Р = 12;
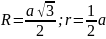
 ,
В = 6,
Р = 12;
,
В = 6,
Р = 12;
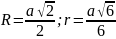
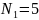 ,
,
В = 20,
Р = 30;
,
,
В = 20,
Р = 30;
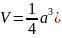

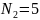 ,
В = 12,
Р = 30;
,
В = 12,
Р = 30;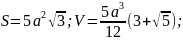
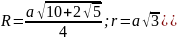


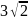 см
см см
см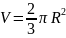
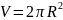
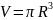
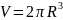
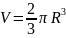
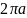

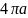
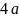
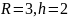
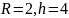
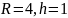


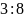
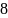 см
см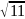 см
см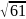 см
см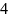 см
см
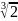

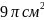
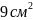
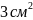
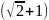 см
см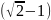 см
см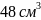
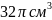
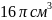

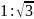
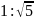
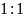
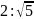

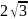 см
см см
см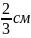
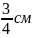
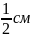
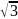 разів
разів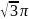 разів
разів см
см