II. Оптимізація виробничої програми
Оптимальна програма визначається на основі формування задачи лінійного програмування і її розв’язку симплексним методом. Математична модель задачі складається з трьох частин:
системи ресурсних обмежень -
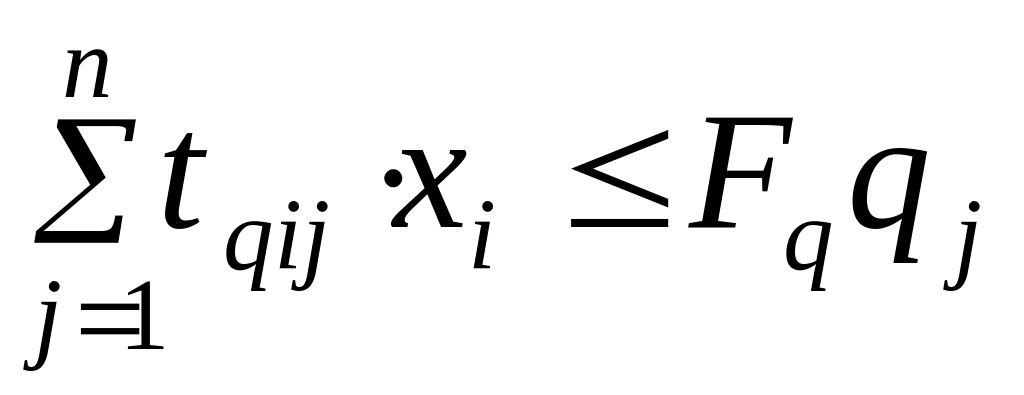;системи обмежень, зумовлених попитом (хі ≤
)
і договорами поставок (хі
≥
);цільової функції Рі хі → max,
де
– фактична машиномісткість і-го
виду продукції за j-ою
групою устаткування, м-год./шт.; хi
– шукана
кількість продукції i-го
виду (A, B і
C), шт./рік;
Fq
– ефективний (корисний) фонд часу одиниці
устаткування, год./рік; qj
– кількість устаткування j-го
виду;
–
прогнозний попит на продукцію i-го
виду (A, B, C),
шт./рік;
–
обов’язкові поставки продукції i-го
виду за укладеними договорами, шт./рік;
Pi
– прибуток
від реалізації одиниці продукції,
грн./шт.
Ефективний (корисний) фонд часу приймається однаковим для всіх видів устаткування і визначається за формулою
,
де Fн
– номінальний (режимний) фонд часу,
год./рік;
–
втрати робочого часу, необхідні для
планових ремонтів устаткування у
відсотках Fн,
Кр=5...8%.
,
де f – кількість робочих змін за добу (раціонально f =2); τ – тривалість робочої зміни (при п’ятиденному робочому тижні τ =40/5=8 год.); Тр і Тс – кількість робочих і святкових днів в наступному році (за календарем); Δτ – скорочення робочого дня перед законодавчо визнаним святом, Δτ =1 год.
Після обчислення F його значення можна заокруглити (F ≈ 4000 год./рік) для спрощення наступних розрахунків.
Прибуток на одиницю продукції (Рj) визначається умовно на основі вихідних даних завдання за формулою:
де Pi
– прибуток з розрахунку на 1 м-год.
машиномісткості продукції i-го
виду (див. завдання), грн./м-год;
– сумарна машиномісткість одиниці
продукції.
Прогнозний попит на продукцію A, B і C ( ) визначається за відповідними функціями тренду – як сума значень Nt в наступних чотирьох кварталах (див. табл. 1.2). Оскільки нова продукція (Сн) є покращеним аналогом (за призначенням) продукції С, то можна вважати, що загальний попит на продукцію С і Сн не перевищить найвищі досягнення (максимальні значення) реалізації продукції С в минулі квартали, тобто:
За вихідними даними завдання та результатами попередніх розрахунків складається математична модель (табл.2.1.)
Таблиця 2.1.
Математична модель (приклад)
Системи обмежень і цільова функція |
Наявні ресурси тис. маш.-год. / рік |
||||||
Всього |
Витрати на виконання договірних зобов’язань: |
Вільний залишок |
|||||
х1 |
х2 |
х3 |
х4 |
п.3 – п.4 |
|||
Ресурсні обмеження |
2,3х1+3,0х2+2,8х3+2,4х4≤4·12 |
48 |
11,5 |
9 |
0 |
0 |
27,5 |
3,8х1+2,0х2+3,4х3+3,6х4≤4·14 |
56 |
19 |
6 |
0 |
0 |
31 |
|
3,9х1+4,0х2+2,9х3+3,1х4≤4·18 |
72 |
19,5 |
12 |
0 |
0 |
40,5 |
|
2,6х1+2,8х2+1,9х3+2,3х4≤4·9 |
36 |
13 |
8,4 |
0 |
0 |
14,6 |
|
1,6х1+1,5х2+2,0х3+2,4х4≤4·7 |
28 |
8 |
4,5 |
0 |
0 |
15,5 |
|
1,6х1+2,5х2+3,0х3+2,8х4≤4·14 |
56 |
8 |
7,5 |
0 |
0 |
40,5 |
|
1,3х1+2,6х2+2,8х3+2,6х4≤4·10 |
40 |
6,5 |
7,8 |
0 |
0 |
25,7 |
|
2,3х1+2,6х2+1,8х3+1,5х4≤4·11 |
44 |
11,5 |
7,8 |
0 |
0 |
24,7 |
|
Обмеження по попиту |
5,0 ≤ х1≤ 22,97 |
|
1 |
0 |
0 |
0 |
17,97 |
3,0 ≤х2≤25,56 |
0 |
1 |
0 |
0 |
22,56 |
||
х3 ≤ 1,66 |
0 |
0 |
1 |
0 |
1,66 |
||
х3+х4 ≤15,54 |
0 |
0 |
1 |
1 |
15,54 |
||
Цільова функція |
65,96х1+75,6х2+90,64х3+82,85х4→max |
|
|||||
У відповідності до наведеної моделі складається матриця коефіцієнтів: стовпчики позначаються відповідними дійсними змінними х1, х2, х3, х4, а стрічки – штучними змінними х11, х12, ... х1n, як показано в табл.2.2., без обмежень за договірними зобов’язаннями. В стовпчику наявних ресурсів приводяться значення їх залишку. Далі задача розв’язується за наступним алгоритмом.
В рядку цільової функції визначити максимальне значення поміж Рі. В наведеному прикладі Рma = 90,64 Стовпчик в якому знаходиться Рmax називається базовим (х3) і виділяється поміж інших.
Знайти мінімальне додатнє відношення j-го ресурсу до відповідного елемента базового стовпчик. Відповідна стрічка матриці (х21) називається базовою, а її елемент, який знаходиться на перетині з базовим стовпчиком (а21,3 =1) – опорним.
Таблиця 2.2.