3. Критерий с.Н.Журкова. Кинетическая концепция прочности твердых тел

Многочисленные исследования, проведенные С.Н.Журковым с сотрудниками, показали, что временная зависимость прочности присуща всем твердым телам и при постоянной (комнатной) температуре при растяжении имеет вид:

. (3.3.1)

Вопрос об истинной зависимости τ от σ важен, так как он в значительной мере определяет ту или иную интерпретацию данных по долговечности, преследующую цель вскрытия природы процесса разрушения тела.

Необходимо отметить, что вопрос о достоверности связи τ=f(σ) связан, в первую очередь, со значительным разбросом экспериментальных данных. Долговечность одинаковых образцов, испытанных при одном и том же напряжении при идентичных условиях, могут различаться до 100 раз. Так что обработка данных требует внимания и тщательности.

Широко используется метод статистической обработки по способу наименьшего квадратичного отклонения. К настоящему времени исследовано более сотни различных материалов: металлы, полимеры, стекла, бетоны, древесина, композиты и др., и подтверждено, что в достаточно широком диапазоне напряжений зависимость lgτ–σ остается линейной, т.е. подтверждается зависимость (3.3.1). Изучение зависимости механической долговечности от температуры является особенно важным для развития кинетической концепции разрушения твердых тел. Было обнаружено, что линейная зависимость lgτ–σ оправдывается не только при комнатной, но и при других температурах (см. рисунок 3.3.1).

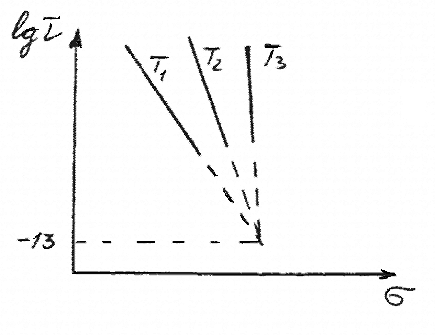
Т₁>Т₂>Т₃

Рисунок 3.3.1 – Линейные зависимости механической долговечности

Выявлена существенная особенность вида температурно-силовой зависимости долговечности: а именно, веерообразность семейства прямых, соответствующих различным температурам испытаний, когда эти прямые при экстраполяции пересекаются в одной точке – полюсе, причем, что очень важно, для разных материалов полюсы лежат при практически одном и том же значении долговечности ≈10^-13 сек.

Изменения долговечности при разных температурах позволили определить температурные зависимости долговечности твердых тел при фиксированных разрывных напряжениях σ. Зависимости lgτ от 1/T (см. рисунок 3.3.2) оказались линейными и при разных σ образуют «температурный веер» с полюсом.

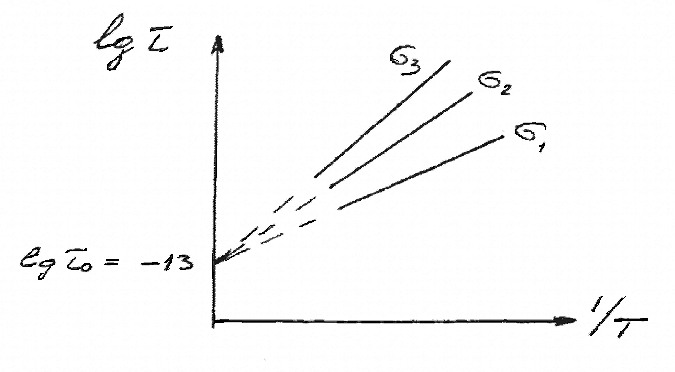σ₁<σ₂<σ₃

Рисунок 3.3.2 – Температурные зависимости долговечности

Зависимость lgτ от 1/T имеет вид:

,

или ,

где b₁(σ)=2,3b(σ).

Умножив числитель и знаменатель экспоненты на постоянную Больцмана k=1,38×10^-16 эрг/град и, обозначив kb₁(σ)=U(σ), получим:

. (3.3.2)

Проведено изучение этой зависимости на большом числе материалов и определено, что ее можно считать достаточно общей и справедливой для многих твердых тел.

Для определения τ₀ требуется найти ординату полюса, что сопряжено со сравнительно далекой экстраполяцией экспериментальных участков прямых, приводящей к небольшой точности. Значение U(σ) может быть вычислено из наклона прямых на графике lgτ от 1/T:

.

В этом случае величина U(σ) измеряется в эргах и относится к единичному событию атомного масштаба (по смыслу постоянной Больцмана). Если же заменить постоянную Больцмана на универсальную постоянную R=kN_A=2×10^-3 ккал/(моль×град), то получим для U (σ) в ккал/ моль:

.

Величину U(σ) назвали энергией активации процесса разрушения.

Как оказалось, связь U и σ линейна:

U(σ)=U₀–γσ , (3.3.3)

где U₀ – значения при σ=0;

γ – коэффициент, определяемый из наклона графика U(σ).

Обобщая уравнения (3.3.2) и (3.3.3), пришли к закономерности:

. (3.3.4)

Легко видеть, что в уравнении (3.3.1)

, α=γ/RT.

Опыт показывает, что для всех материалов, независимо от их химического состава, типов сил связи и структуры, предэкспоненциальный множитель τ₀ остается (в пределах точности его определения), примерно, постоянным, лежащим в интервале 10^-12 – 10^-14 сек (в среднем τ₀≈10^-13 сек), и совпадает по десятичному порядку с периодом тепловых колебаний атомов в телах. Начальный энергетический барьер U₀ меняется от материала к материалу (для полиэтилена U₀=25 ккал/моль, для молибдена U₀=170 ккал/моль) и при этом оказывается близким к величине энергии активации распада межатомных связей в твердых телах: в металлах – к энергии сублимации, в полимерах – к энергии активации процесса термодеструкции. С другой стороны, U₀ для данного материала не зависит от всевозможных структурных изменений. Иначе говоря, τ₀ и U₀ – нечувствительны к изменениям структуры.

Единственным «структурночувствительным» коэффициентом является коэффициент γ.

В ходе экспериментов также отмечена необратимость процесса разрушения, а также тот факт, что временная зависимость прочности не является следствием только лишь влияния окружающей среды.

Все эти свойства позволили сформулировать основные положения кинетической концепции прочности.

Главным действующим фактором при разрушении оказывается не внешняя сила, а тепловое движение атомов, порождающее энергетические флуктуации. Именно флуктуации разрывают межатомные связи, что и ведет к разрушению тела. Внешняя сила выступает здесь в качестве своеобразного «вентиля», открывающего флуктуациями возможность разрывать связи и «запирающего» возможность их флуктуационной же рекомбинации, т.е. внешняя сила обеспечивает направленность разрывного действия флуктуаций, без чего не может развиваться разрушение. Это существенно меняет представление об энергетике процесса разрушения. При термофлуктуационном разрушении значительная, а иногда и основная доля работы по разрушению выполняется не внешней силой, а за счет запаса тепловой энергии тела. Работа внешней силы может составлять здесь малую долю. Все это позволяет говорить о механической прочности тела как о таком его свойстве, которое в основе своей имеет не «чисто механическую» природу, обусловленную чисто силовым взаимодействием атомов, а «кинетическую» природу, связанную с тепловым движением атомов. Это дает основание говорить о кинетической природе прочности и противопоставлять термофлуктуационный механизм разрушения чисто механическому. Основные положения концепции подтверждены прямыми физическими методами исследований.

В ходе экспериментов отмечены усложненные случаи разрушения, которые не приводят при их анализе к отрицанию основных положений кинетической концепции прочности.

Искривление зависимости lgτ от в области малых σ (см. рисунок 3.3.3) отмечалось во многих работах.

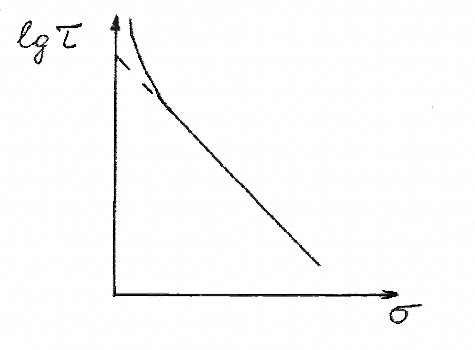
Рисунок 3.3.3 – Искривление зависимости в области малых σ

Эффект этот вполне естественен, и его следует ожидать для любых твердых тел, так как при малых σ уравнение (3.3.4) неприменимо. Ограниченность применимости формулы (3.3.4) заключается в том, что она, описывая процесс термофлуктуационного распада межатомных связей, не учитывает возможности их восстановления. Доля же актов восстановления связей, естественно, возрастает с уменьшением напряжения, уравниваясь в пределе (при σ=0) с количеством актов распада, исключает накопление разрывов связей и развитие разрушения. Вторая причина заключается в том, что предэкспоненциальный множитель τ₀ лишь для элементарных актов может считаться постоянным. Если же описывать процесс разрушения тела как последовательность термофлуктуационных распадов связей, то после соответствующих математических выкладок, учитывающих постепенное изменение напряжения на разрываемых связях, получается формула типа (3.3.4), но с предэкспоненциальным множителем вида:

τ_а×φ(T, σ), (3.3.5)

где τ_а≈10^-13 сек – период колебания атомов (τ_а≈h/kT, h - постоянная Планка);

φ(T, σ) – некоторая степенная функция от температуры и напряжения.

При средних значениях T и σ значение φ(T, σ) близко к 1. При малых σ функция φ(T, σ) влияет на величину τ заметно, «завышая» долговечность по сравнению с формулой (3.3.4).

Ряд материалов во всем диапазоне σ не проявляет линейной зависимости lgτ–σ: она криволинейна (см. рисунок 3.3.4).

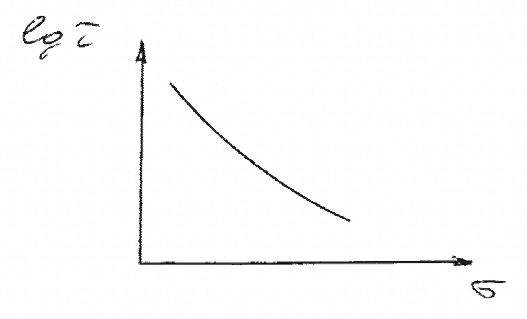
Рисунок 3.3.4 – Криволинейная зависимость lgτ от σ

В основном, такая зависимость характерна для структурно-нестабильных материалов. Вероятнее всего долговечность таких материалов можно описать выражением типа (3.3.4), но с переменными параметрами (прежде всего γ). Таким же образом можно описать и следующие особенности: выпадение отдельных прямых из общего веерообразного семейства (см. рисунок 3.3.5а) и изломы (см. рисунок 3.3.5б).

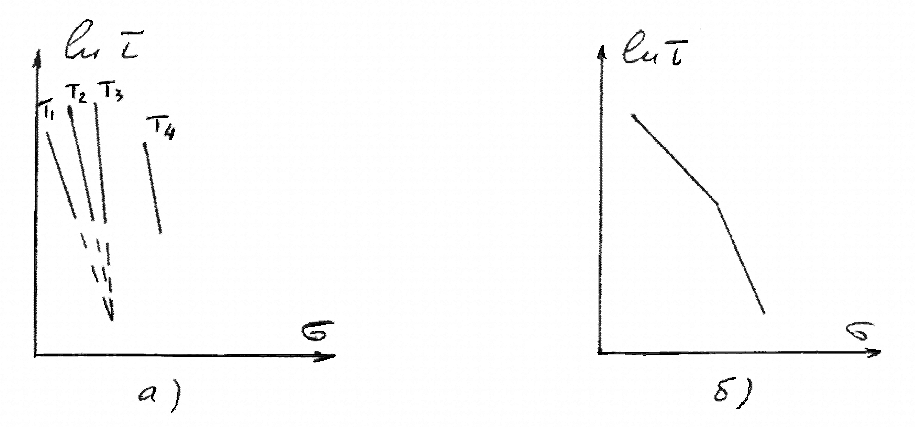
Рисунок 3.3.5 – Особенности зависимостей долговечности

В литературе отмечен еще один случай отклонений от закономерности (3.3.4): «эффект смещения полюса» (см. рисунок 3.3.6).

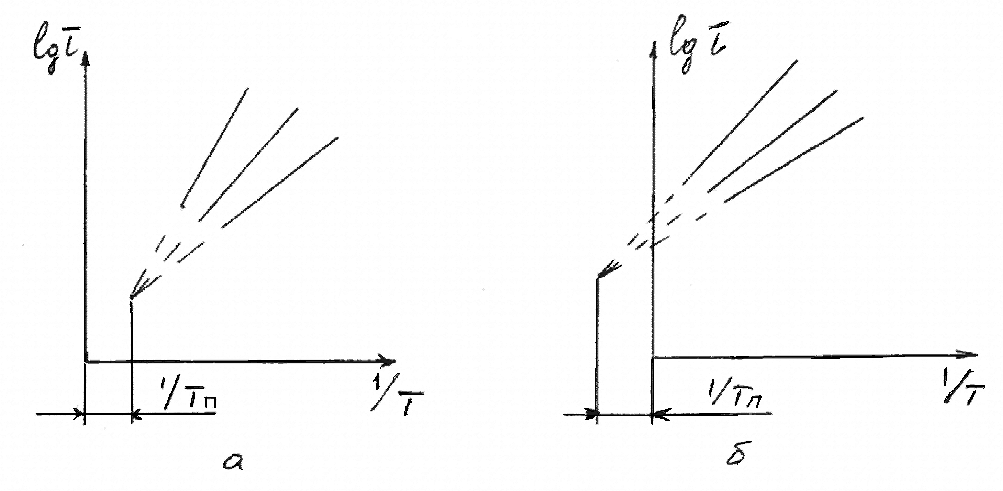
Рисунок 3.3.6 – "Эффект смещения полюса" зависимостей долговечности

Зависимость τ(σ, Т) в этом случае изображается в координатах lgτ–1/T семейством прямых, сходящихся при линейной экстраполяции в одну точку – «полюс», который находится, однако, не на оси ординат, как этого требует закономерность (3.3.4), а сдвинут в ту или иную сторону на расстояние 1/T_п. Этот эффект вполне объясним, если предположить зависимость коэффициента γ от σ и Т. Как видно, отступления от закономерности (3.3.4) вполне объяснимы на основе представлений о термофлуктуационной природе процесса разрушения.

Кроме испытаний на растяжение при постоянной нагрузке исследовалась долговечность при сложных режимах нагружения. При этом предложено (а это подтверждено экспериментально) исходить из принципа суммирования повреждений, т.е. из предположения о необратимости разрушающего действия нагрузки. Необратимый характер процесса разрушения приводит к уменьшению ресурса долговечности материала, побывавшего под нагрузкой. Если напряжение σ действовало в течение времени Δt₁, то соответствующее относительное уменьшение долговечности можно положить равным Δt₁/τ.

В следующий период Δt₂ действия той же доли нагрузки σ доля уменьшения долговечности составит Δt₂/τ и т.д. Разрыв ожидается тогда, когда сумма относительных уменьшений долговечности станет равной единице:

.

Если σ=σ(t), то

, (3.3.6)

где t_p – время наступления разрыва.

Зависимость (3.3.6) называют законом Бейли.

Для случая , где - скорость роста напряжений, t – время нагружения:

.

Учитывая, что , получим: .

Так как τ_p<<А, то .

Тогда после логарифмирования имеем:

(3.3.7)

Как видно, разрывное напряжение является линейной функцией , что неоднократно наблюдалось при испытании материалов. Возможность определять долговечность по результатам испытаний при нарастающей нагрузке подтверждена экспериментально.

Исследования долговечности при кручении, как одном из видов сложного напряженного состоянии, также подтвердили вывод о кинетической природе твердых тел. Рассмотренная концепция находится на этапе дальнейшего подтверждения и совершенствования, в частности, в работах Г.М.Бартенева.