3 Теория процессов накопления повреждений. Кинетическая природа прочности твердых тел

В настоящее время является общепринятой точка зрения, что разрушение тела не есть мгновенный акт, а представляет собой процесс, подготовляющийся с самого начала нагружения тела за счет накопления в последнем повреждений. Особенно отчетливо это проявляется в условиях напряжений, переменных во времени по величине, а тем более по знаку; в условиях высокотемпературной ползучести и пластического деформирования.

3.1 Критерий Хоффа

Хофф исследовал вопрос о длительной прочности при одноосном растяжении стержня. Вследствие удлинения образца по мере роста деформации ползучести поперечное сечение образца все время уменьшается, что приводит к увеличению напряжений в сечении и, следовательно, к увеличению скорости ползучести. В результате этого процесса по истечении некоторого времени площадь поперечного сечения стержня должна уменьшиться до нуля. Этот промежуток времени Хофф предлагает считать критическим временем длительной прочности.

Истинная скорость ползучести

; (3.1.1)

σ_ист=σ_о(1+ε); ε_ист=ln(1+ε).

Пусть ,

где В₁ и m – постоянные, определяемые из эксперимента.

Обозначив 1+ε=R, получим:

.

После интегрирования и нахождения постоянной интегрирования из условия τ=0, R=1 имеем:

. (3.1.2)

Если R→∞, то

, (3.1.3)

где - скорость деформации ползучести в начале испытаний.

Тогда

τ=τ_кр(1-R^-m) (3.1.4)

или

l₀/l=F/F₀=(1-τ/τ_кр)^1/m. (3.1.5)

Формула Хоффа проверялась экспериментально на алюминиевом сплаве 3S–H18 и показала хорошее соответствие теоретических и экспериментальных значений. Вместе с тем, она неприемлема в общем случае для любого напряженного состояния, например, при кручении изменение площади не происходит. Ряд материалов разрушается хрупко (до 1 %), когда изменение площади мало. Из изложенного следует, что концепция Хоффа имеет ограниченную область применения.

3.2 Критерий Качанова

Л.М.Качанов поставил перед собой цель найти продолжительность жизни тела (вообще говоря, произвольной формы), работающего в условиях ползучести, независимо от того, имеет ли разрушение вязкий или хрупкий характер.

Развивая теорию Хоффа, он рассматривает процесс разрушения при растяжении как процесс трещинообразования, развивающийся на фоне растущих деформаций ползучести. Вводится скалярная величина 0≤ψ≤1, характеризующая поврежденность сечения вследствие образования микротрещин, и, следовательно, истинная площадь сечения равна ψF.

В начальный момент, когда еще повреждений нет, ψ=1, а в момент хрупкого разрушения ψ=0. Следовательно, критическое время τ_{кр хр} является временем, в течение которого ψ уменьшается от единицы до нуля.

Качанов ввел следующее уравнение:

, (3.2.1)

где А и n – экспериментальные константы.

После интегрирования и определения константы интегрирования из условия при τ=0, ψ=1 получаем:

. (3.2.2)

При ψ=0

(3.2.3)

В общем случае, когда происходят одновременно два процесса - трещинообразование и ползучесть, с учетом уравнения (3.1.5) имеем:

. (3.2.4)

Учитывая, что P/F₀=σ_о, получим:

.

Интегрируя, будем иметь:

.

Здесь учтено, что , так как при τ=0 σ_max=σ₀.

При ψ=0 τ=τ_(кр). Отсюда следует, что

(m≠n) . (3.2.5)

Уравнение имеет смысл при τ_(кр)≤τ_кр.

Отсюда следует:

,

или

; ; ,

или, наконец,

.

Если напряжения превышают , то разрушение происходит вязкое, согласно решению Хоффа. При напряжениях меньших, чем , разрушение происходит хрупко, но при больших или меньших деформациях, определяемых из (3.1.5) при τ=τ_(кр).

На рисунке 3.2.1 изображена кривая длительной прочности.

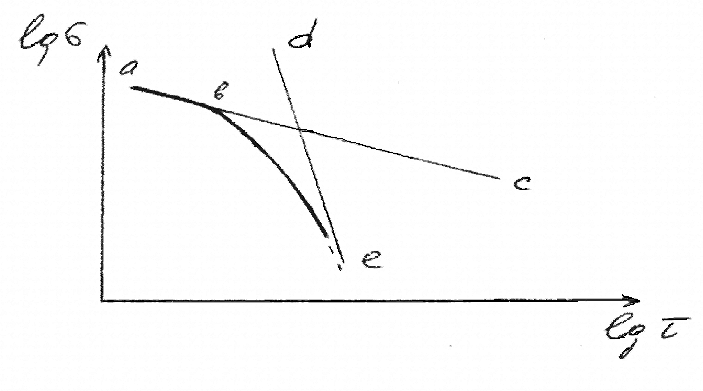
Рисунок 3.2.1 – Кривая длительной прочности

Прямая ac соответствует вязкому, а асимптота de – чисто хрупкому разрушению.

Кривая длительной прочности плавно переходит в прямую aс в точке b и асимптотически подходит к прямой de. Постоянные A и n находятся по положению линии de.

Рассмотрим случай m=n.

Перепишем формулу (3.2.5) в следующем виде:

.

Имея в виду формулу , получаем: .

При этом разрушение всегда хрупкое (при ψ =0) и происходит при одной и той же деформации, равной 1-(l/l_(кр))^m, где l_(кр) – длина стержня при разрушении.

В исследовании Л.М.Качанова накопление дефектов учитывается в явной форме при помощи функции ψ, однако никакой конкретизации физической природы возникновения и развития трещин не производится.