2.6.3 Критерии усталостной прочности

Многие детали машин в процессе работы испытывают действие переменных во времени напряжений. Если эти напряжения превышают определенный уровень, то в детали начинают происходить необратимые изменения, которые приводят к образованию трещин. Трещина развивается до мгновенного разрушения. Это явление называется усталостью (см. рисунок 2.6.3.1).

Рисунок 2.6.3.1 – Кривая усталости

N – количество циклов;

- предел усталости (на базе N=10⁷ циклов).

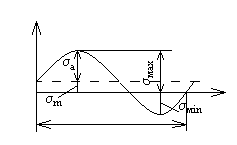
На рисунке 2.6.3.2 даны характеристики цикла.

T

Рисунок 2.6.3.2 – Характеристики циклов нагружения

Т – период цикла;

- амплитудное значение напряжений;

- среднее значение напряжений;

, - максимальное и минимальное значение напряжений.

;

;

r = - коэффициент асимметрии.

Если , то r=-1 и цикл называется симметричным. Тогда - предел выносливости при симметричном цикле.

Если =0, = , то r=0 и цикл называется пульсирующим.

r -1 – асимметричный цикл.

- предел выносливости при асимметричном цикле.

Диаграмма предельных напряжений (диаграмма Хея - Зодерберга) при асимметричном цикле представлена на рисунке 2.6.3.3.

σ_a

Рисунок 2.6.3.3 – Диаграмма предельных напряжений

Кривую предельных напряжений обычно аппроксимируют прямой, эллипсом, гиперболой и т.д. При линейной аппроксимации:

, (2.6.3.1)

где - статическая прочность.

При повторно – переменном или нестационарном механическом нагружении в условиях сложного напряженного состояния реализуется бесконечное множество различных сочетаний, которые могут отличаться друг от друга, как пределами изменения абсолютной величины, так и частотой. В этих условиях задача о критериях эквивалентности в отношении усталости значительно усложняется и в общей постановке становится практически неразрешимой. Поэтому известные теории усталостной прочности установлены применительно к отдельным наиболее простым случаям нагружения и, как правило, являются результатом обобщения теорий статической прочности на случай усталости. Для подтверждения правомерности использования критериев статической прочности в расчетах на усталость обычно ссылаются на то, что отношения предельных напряжений при чистом сдвиге и растяжении- сжатии в условиях усталости и статического нагружения для большинства материалов практически совпадают.

Если компоненты тензора напряжений изменяются по симметричному циклу, то критерии прочности в расчетах на усталость отличаются лишь выбором констант материала.

Исходя из линейной зависимости между октаэдрическими касательными и нормальными напряжениями (гипотеза Боткина - Миролюбова), С.В.Серенсен за критерий усталостной прочности принимает следующее уравнение:

, (2.6.3.2)

где m= ; , - предел выносливости при сдвиге и растяжении соответственно.

Строят также зависимости в координатах: (рисунок 2.6.3.4).

Рисунок 2.6.3.4 – Критерий усталостной прочности

Для стали опытные данные лучше описываются дугой:

.

Для чугуна – эллипсом:

.

При несимметричных циклах удобно использовать поверхность предельных напряжений в координатах: (см. рисунок 2.6.3.5).

1- линия статического разрушения; 2 – кривая усталости;

3 – кривая длительной прочности; 4 – кривые предельных напряжений.

Рисунок 2.6.3.5 – Поверхность предельных напряжений

Если кривую 1 предельных напряжений аппроксимировать прямой (уравнение 2.6.3.1), тогда для эквивалентных напряжений имеем:

.

В соответствии с гипотезой максимальных касательных напряжений ( ; ; ) имеем:

. (2.6.3.3)

Если кривая 1 – гипербола, то

.

Условие эквивалентности при =const принимает вид:

, (2.6.3.4)

где , , ,

, - пределы изменения касательных напряжений при кручении;

, - пределы изменения нормальных напряжений при изгибе или растяжении – сжатии.

Предложена и такая аппроксимация кривой 1:

,

где , - некоторые коэффициенты, зависящие от состояния поверхности и чувствительности металла к концентрации напряжений.

Тогда для случая сложного напряженного состояния имеем:

.

А.А.Лебедев и Г.С.Писаренко предлагают использовать формулы:

;

, (2.6.3.5)

где ; .

Зачастую .

Критерий (2.6.3.5) проверялся на чугунах и сталях Х18Н9Т и 30ХГСА при наличии асимметрии в условиях плоского напряженного состояния.

Кроме циклической усталости существуют понятия малоцикловая усталость (до N=10²) и термоусталость (циклическая смена температур). Эти виды исследованы недостаточно. Для оценки малоцикловой усталости используется критерий Коффина:

, (2.6.3.6)

где N – число циклов, - размах пластической деформации.

Для оценки термопластичности Кузнецов предложил критерий:

= / ,

где - максимальная линейная пластическая деформация;

- интенсивность пластической деформации;

- константа.