2.5.6 Достоверность теорий прочности

Феноменологический подход к разработке механических теорий прочности и их большое разнообразие предполагают обязательную экспериментальную оценку достоверности применяемого критерия. Среди экспериментальных оценок можно назвать следующие:

а) проверка по особым случаям напряженного состояния (двухосное равномерное растяжение и сжатие, всестороннее равномерное сжатие);

б) проверка по отдельным видам напряженных состояний (сдвиг, радиальное сжатие);

в) сопоставление набора физических результатов при различных напряженных состояниях с теоретическим контуром по каждому материалу;

г) сопоставление фактических и теоретических значений разрушающих напряжений в безразмерных координатах, т.е. по группе исследуемых материалов;

д) построение розеток ошибок теоретических расчетов;

е) количественная оценка точности каждой теории прочности по определенному интервалу напряженных состояний и набору материалов.

2.5.6.1 Особые случаи напряженного состояния:

а) ₁=₂>0, ₃=0;

б) ₂=₃<0, ₁=0;

в) ₁=₂=₃<0.

В случае всестороннего равномерного сжатия (в) эквивалентные напряжения по I-IV теориям прочности равны:

^I_экв=0; ^II_экв=^III_экв=^IV_экв=0.

Трудно представить _экв=0. Но горные породы, действительно, выдерживают без разрушения весьма значительные напряжения, которые могут в десятки раз превышать их прочность на линейное сжатие. Подобные результаты получены и при исследовании прочности материалов при гидростатическом давлении. Однако разрушение при всестороннем неравномерном сжатии все же имеет место. Можно предполагать, что разрушение наступает за счет дефектов и неоднородности материалов, которые приводят к перераспределению напряжений, что и будет являться причиной разрушения.

Все классические теории прочности для двухосного равномерного растяжения и сжатия дают одно и то же значение, которое приравнивается к пределу прочности на растяжение и сжатие.

Фактическое значение прочности при двухосном равномерном растяжении и сжатии по многим материалам весьма близко к пределу прочности при линейном растяжении и сжатии. В то же время, для ряда структурно-неоднородных материалов (кермет на основе карбида кремния, пьезокерамика, графиты и т.д.) получены экспериментальные значения напряжений при ₁/₂=1 и –1 заметно отличающиеся от _р и _с, что дает возможность в этих точках провести оценку надежности ряда теорий прочности.

2.5.6.2 Оценку надежности теорий прочности можно осуществить и по другим точкам, эксперимент в которых достаточно прост. К таким экспериментам относятся сдвиг и радиальное сжатие. Сдвиг реализуется при кручении трубчатых образцов, радиальное сжатие при сжатии по радиусу цилиндрических образцов.

При сдвиге напряженное состояние следующее:

₃=-₁=_к; ₂=0; ₃/₁=-1.

При радиальном сжатии (в центре цилиндра):

₃=-3₁=6P/×d×l; ₂=0; ₃/₁=-3.

где Р – разрушающая нагрузка, d и l – диаметр и длина образца.

На рисунке 2.5.6.1 приведена фактическая и расчетная прочность материалов на сдвиг.

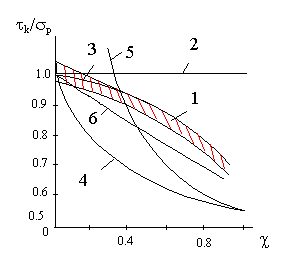
1 - доверительная зона экспериментальных данных;

2 – I теория;

3 – теория ТПИ;

4 – теория Кулона-Мора;

5 – теория Баландина;

6 – теория Лебедева-Писаренко.

Рисунок 2.5.6.1–Прочность материалов на сдвиг

Из рисунка 2.5.6.1 видно, что в наилучшем соответствии критерии ТПИ и Лебедева-Писаренко. В таблице приведены результаты испытаний при радиальном сжатии.

Таблица 2.5.4.3 – Результаты испытаний при радиальном сжатии

Материал		р/1	По Баландину		По Боткину		По Лебедеву и Писаренко
			р/1	, %	р/1	, %	р/1	, %
Сплав АС 418	0,04	0,64	0.15	70.6	0.58	9.4	0,64	0
Сплав ЮНКД-24	0,08	0,64	0,28	56,2	0,65	1,6	0,66	3,2
К-17-2	0,16	0,73	0,52	28,8	0,79	8,2	0,72	1,4
К-20-2	0,17	0,75	0,55	26,7	0,81	8,0	0,73	2,7
К-18-2	0,18	0,81	0,58	28,4	0,83	2,5	0,74	8,6
К-21-22	0,19	0,71	0,62	12,7	0,85	19,7	0,76	7,4
Серый чугун НВ 190	0,26	0,90	0,79	12,2	0,97	7,8	0,91	1,2
Серый чугун НВ 110	0,31	0,82	0,91	11,0	1,06	29,3	0,93	13,4
Сталь 9ХСНРС62	0,63	1,47	1,60	8,8	1,63	10,9	1,54	4,8
Сталь 9ХСНРС50	0,71	1,63	1,74	6,8	1,76	8,0	1,55	4,9
Среднее отклонение				26,82		10,54		4,74

Из таблицы видно, что средняя относительная ошибка  по всем материалам минимальная по критерию Лебедева–Писаренко.

2.5.6.3 Если эксперимент проведен при разных сочетаниях главных напряжений, то составляется таблица в виде выше приведенной и определяется критерий, у которого наименьшее среднее отклонение.

2.5.6.4 Достоверность критерия можно повысить, если провести расчет по группе исследованных материалов (например, пластмассы К-17-2, К-20-2, К-18-2 в таблице).

2.5.6.5 Наиболее полное представление о достоверности теорий прочности дают розетки ошибок теоретических расчетов на прочность.

При плоском напряженном состоянии такие розетки строятся в следующем порядке (см. рисунок 2.5.6.2).

а) б)

а) СBD – теоретический контур прочности, точка А – эксперимент;

б) розетки ошибок по теории Баландина.

Рисунок 2.5.6.2 – Розетки ошибок теоретических расчетов на прочность

По построению ОА – фактический радиус прочности, ОВ – теоретический, АВ – абсолютная разность, ОА/ОВ – относительная разность между фактической и теоретической прочностью при известном соотношении главных напряжений.

Усредняя фактические результаты экспериментов, можно подсчитать отношение теоретического радиуса прочности к фактическому для каждого соотношения главных напряжений, и отложить это отношение по соответствующему лучу. Соединив соответствующие точки, получим розетку теоретических ошибок. На один чертеж можно нанести кривые по любым теориям прочности и для любого исследованного материала.

2.5.6.6 Зная ₁ и ₁ при разных соотношениях n=₃/₁, можно определить величину средней квадратической ошибки в исследованном диапазоне напряженных состояний для данного материала:

,

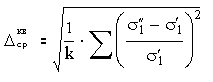где k – количество напряженных состояний, при которых определялась фактическая прочность материала.

Строится таблица, и определятся достоверность P=1-^кв_ср соответствующей теории прочности.

Многочисленные исследования показывают, что при плоском напряженном состоянии наибольшей достоверностью отличаются критерии Лебедева-Писаренко и ТПИ. При объемном напряженном состоянии требуется дальнейшая экспериментальная проверка.