2.5.5 Статистические теории прочности

2.5.5.1 Теория прочности С.Д.Волкова исходит из положения о том, что существует два рода напряжений:

а) напряжения, вызванные внешними нагрузками в твердом теле (I рода);

б) самоуравновешивающиеся напряжения – микронапряжения (II рода).

Рассматривается модель микроскопически неоднородной среды. Возникающая пластическая деформация – результат совместного действия напряжений I и II рода. Определяется вероятность развития разрушений.

Эта теория формулируется так: критическое напряжение I рода зависит от нормального напряжения, действующего в плоскости скольжения, и от гидростатического давления:

_s =  - (_ + _o), (2.5.5.1)

где _s - критическое касательное напряжение I рода на площадке с нормалью ,

_ - нормальное напряжение на этой площадке;

_o - гидростатическое давление;

, ,  - константы материала.

2.5.5.2 Статистический критерий опасности разрушения, предложенный Д.М.Шуром, основывается на следующих исходных положениях:

а) сопротивление отрыву не зависит от касательного напряжения;

б) сопротивление отрыву по различным направлениям является случайной величиной;

в) вероятность повреждения равна нулю, если напряжение сжимающее.

Для хрупко-пластичеких материалов:

_экв=(1-)_экв+_экв, (2.5.5.2)

где _экв - эквивалентное напряжение по I теории прочности;

_экв - эквивалентное напряжение по энергетической теории прочности.

2.5.5.3 А.А.Лебедев и Г.С.Писаренко для структурно-неоднородных материалов указывают на необходимость рассматривать их сопротивление с учетом статистических закономерностей.

Критерий прочности записывается в виде:

_iQ+(1-)₁P=_р, (2.5.5.3)

где Q и P – некоторые функции, отражающие статистические закономерности деформирования и разрушения (Q учитывает особенности возникновения трещин, P – особенности их развития и распространения).

Зарождение новых трещин происходит под влиянием процессов, протекающих в микро - и субмикрообъемах материала. Можно предположить, что влияние при этом статистических факторов несущественно, и принять Q=1. Статистический аспект прочности в основном проявляется в процессе развития трещин, поэтому связать его целесообразно только с нормальным напряжением _1, как критерием их распространения.

Учет этого аспекта более важен для хрупких материалов, структура которых, как правило, характеризуется кроме свойственной всем материалам структурной неоднородности наличием микротрещин, пустот и других существенных дефектов.

Решая вероятностную задачу о прочности неоднородного тела, получаем:

P=A^1-J,

где A=(1-q/q)^ - константа, зависящая от характера имеющихся в материале дефектов и, следовательно, отражающая статистическую сущность процесса разрушения, - от размеров тела; q – вероятность нарушения сплошности;  - константа, J – параметр напряженного состояния, имеющий смысл жесткости нагружения;

.

Тогда критерий имеет вид:

_i+(1-)₁A^1-J=_р. (2.5.5.4)

Статистическая сущность функции Р подтверждается корреляцией константы А с коэффициентом гомогенности m в теории хрупкой прочности Вейбулла.

Действительно, при =0: А=_р/_k.

В соответствии с теорией Вейбулла отношение предельных напряжений при чистом изгибе балки прямоугольного сечения к предельным напряжениям при кручении круглого стержня и одинаковой вероятности разрушения образца определяется выражением

Если принять влияние градиентов напряжений при изгибе и кручении одинаковыми, то можно получить:

. (2.5.5.5)

Зависимость (2.5.5.5) нашла экспериментальное подтверждение. Таким образом, константу А можно легко определить по результатам весьма простых в методическом отношении опытов, например, испытании образцов разных размеров. Отмечено, что при m<10 пренебрежение влиянием дефектов структуры приводит к заметным ошибкам. А=0,65…0,85, в среднем 0,75. Критерий (2.5.5.4) нашел экспериментальное подтверждение для таких материалов, как графит, чугуны, хрупкие термореактивные пластмассы и пр.

2.5.5.4 Гриффитс показал, что разрушение, начинающееся вблизи концов случайно ориентированных эллиптических трещин, приводит к макроскопическому критерию разрушения по напряжению, графически представленному на рисунке 2.5.5.1:

₁=_р, при 3₁+₂>0;

(₁-₂)²+8_p(₁+₂)=0, при 3₁+₂<0. (2.5.5.6)

Таким образом, начав с субмакроскопического уровня, можно формулировать макроскопический критерий разрушения. Очевидный недостаток критерия (2.5.5.6) в том, что _с/_р=-8 (для многих материалов это не верно), т.е. он требует дальнейшего совершенствования, например, с использованием начальных и мгновенных кривых разрушения.

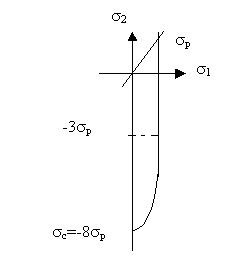
Рисунок 2.5.5.1 – Макроскопический критерий разрушения Гриффитса