2.5.3 Объединенные теории прочности

Ряд исследователей полагают разделять предельную поверхность на ряд поясов: один – цилиндр, другой – конус и т.д.

Концепция о невозможности описания предельного состояния материала одним уравнением наиболее явно выражена в теории прочности Давиденкова-Фридмана. Эта теория основана на двух основных положениях.

Первое положение. В зависимости от характера напряженного состояния материал может разрушаться как от нормальных напряжений (хрупкое разрушение или разрушение отрывом), так и от касательных напряжений (пластическое разрушение – разрушение срезом).

Второе положение. Для каждого материала существует не зависящая от напряженного состояния связь между напряжениями и деформациями в координатах «касательное напряжение - сдвиг». Для пластических материалов конечная ордината кривой деформирования, представляющей собой предельное сопротивление срезу, является константой материала. На рисунке 2.5.3.1 представлены диаграммы механического состояния.

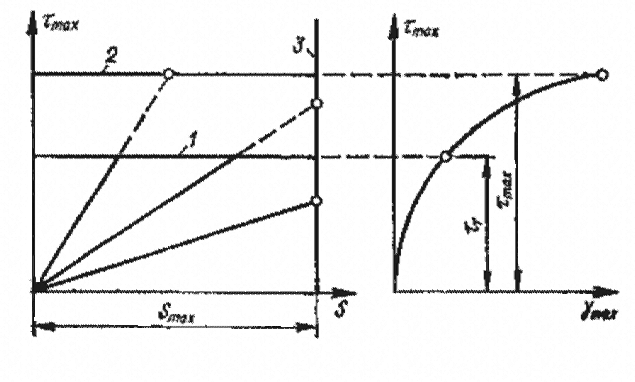
1 – начало текучести; 2 – разрушение сдвигом; 3 – разрушение отрывом; S – эквивалентное напряжение по 2 теории прочности.

Рисунок 2.5.3.1 – Диаграммы механического состояния

Каждому напряженному состоянию соответствует луч, исходящий из начала координат. Так, например, луч, наклоненный к оси под углом, тангенс которого равен ½, соответствует растяжению, 1/2μ – сжатию, 1/(1+μ) – кручению и т.д.

В зависимости от того, какую предельную кривую пересекает луч, определяют вид разрушения (путем отрыва или путем сдвига), а, значит, и теорию прочности, по которой следует вести расчет.

Таким образом, предельная поверхность, соответствующая данной гипотезе, представляет собой равнонаклоненную шестигранную призму, ограниченную с противоположных сторон трехгранной пирамидой.

Пельчинский считает, что при разрушении срезом вместо теории максимальных касательных напряжений лучше использовать энергетическую теорию; в этом случае соответствующая предельная поверхность имеет вид зачиненного цилиндрического карандаша.

Возвращаясь к диаграммам механического состояния, рассмотрим параметры сетки линий материала. Вводятся три коэффициента:

β=τ_к/S; η=τ_т/S; λ=τ_т/τ_к.

Если β>>1, то в целом материал имеет склонность к хрупкому разрушению путем отрыва: σ_р<σ_с.

Если β<<1, то в целом материал имеет склонность к пластическому разрушению путем среза.

Если β≈1, то характер разрушения материала и поведение его в основном зависят от типа напряженного состояния.

Если λ<1, то существует пластическая область, и при каких-то напряженных состояниях имеет место пластическая деформация.

Если λ=1, то произошло вырождение пластической области на диаграмме и, следовательно, материал всегда хрупкий.

Напряженное состояние характеризуется параметром: α=τ_max/S.

Тип излома определяется, с одной стороны, природой материала, характеризуемой коэффициентом β, с другой стороны, напряженным состоянием, характеризуемым коэффициентом α. При β<α имеет место срез, при β>α – отрыв. Условию β=α может соответствовать в одних случаях срез, в других – отрыв, т.е. картина разрушения неустойчива.

Пластическое или хрупкое поведение материала перед разрушением определяется отношением коэффициентов η и α. При η<α перед разрушением имеет место пластическая деформация, такой режим назван «мягким» нагружением. При η≥α материал разрушается хрупко – без предшествующей пластической деформации: такой режим назван «жестким» нагружением.

Я.Б.Фридман обращает внимание на три вида хрупкости материала:

а) хрупкость абсолютная (λ=1), пример, стекло;

б) хрупкость, характеризуемая не только типом разрушения (отрыв), но и отсутствием пластических деформаций перед разрушением; этот вид хрупкости возникает при «мягком» нагружении η<α, даже если λ<1;

в) хрупкость, состоящая в разрушении отрывом, но с предшествующими пластическими деформациями; этот вид хрупкости возникает при «мягком» нагружении (η<α), которое, разумеется, мыслимо лишь при условии λ<1.

Ф.Фишер разработал теорию прочности применительно к серому чугуну. Ее исходные положения:

а) разрушение невозможно без пластической деформации. Критерий прочности при пластической деформации, по мнению автора, описывается энергетической теорией;

б) для чугуна наиболее опасны включения графита;

в) графитные включения хорошо работают на сжатие и совершенно не сопротивляются растяжению.

Предлагается описывать границы прочности тремя уравнениями:

σ₁/χ=σ_с;

(σ₁/χ)²-σ₁σ₂/χ+σ₃²=σ_c²;

σ₂²+σ₃²–σ₃σ₁=σ_c².

Соответствующий комбинированный контур прочности показан на рисунке 2.5.3.2.

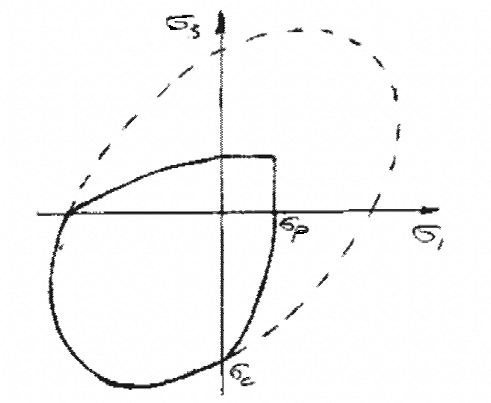
Рисунок 2.5.3.2 – Комбинированный контур прочности

Теория логична. Есть подтверждение этой теории опытами. Но она разработана применительно для чугунов и только для плоского напряженного состояния.

Б.Поль предложил провести усечение пирамиды Кулона-Мора в области растяжения (см. рисунок 2.5.3.3), т.к. σ_р¹>σ_р.

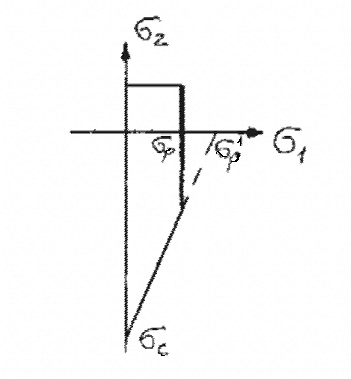
Рисунок 2.5.3.3 – Усечение пирамиды Кулона-Мора в области растяжения