2.5.2 Теории прочности, интерпретирующиеся поверхностями вращения

К этой группе теорий прочности относятся, прежде всего, теории, основанные на энергетических концепциях. При этом следует учитывать, что энергетический критерий (2.4.6) можно получить, принимая за критерий любую величину, которая формально эквивалентна энергии формоизменения (σ_i, τ_окт, J₂′ и др.). Так, условие (2.4.6) можно записать:

σ_i²=σ_р².

Большинство новых энергетических теорий укладывается в рамки высказанной А.Надаи гипотезы о том, что в предельном состоянии октаэдрическое касательное напряжение τ_окт является функцией октаэдрического нормального напряжения σ_окт или среднего σ₀:

τ_окт=f(σ_окт) (2.5.2.1)

или

σ_i=f(σ₀). (2.5.2.2)

В системе координат σ₁, σ₂, σ₃ это уравнение описывает поверхность вращения, равнонаклоненную к осям. Гипотезу Надаи можно рассматривать как более общую формулировку теории прочности Мора.

2.5.2.1 По мнению Шлейхера, опасное состояние материала наступает при определенном значении полной удельной энергии, причем, критическое для нее значение линейно зависит от шарового тензора или от среднего нормального напряжения:

U_уд=а+вσ₀.

В конечном виде:

σ₁²+σ₂²+σ₃²-2μ(σ₁σ₂+σ₂σ₃+σ₁σ₃)+(σ_с–σ_р)(σ₁+σ₂+σ₃)=σ_р+σ_с. (2.5.2.3)

Геометрически – это эллипсоид вращения, центр которого смещен в область трехосного растяжения.

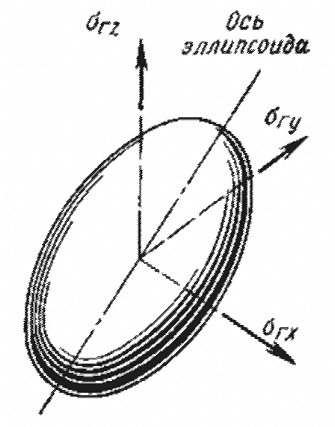
Рисунок 2.5.2.1 - Предельная поверхность – эллипсоид вращения

При σ_р=σ_с критерий превращается в формулу Бельтрами, а при μ=0,5 - в критерий (2.4.6).

Гипотеза Шлейхера плохо подтверждается имеющимися экспериментальными данными и поэтому не получила распространения.

2.5.2.2 Согласно гипотезе Бушинского опасное состояние материала наступает при достижении энергией, состоящей из энергии формоизменения и некоторой части энергии изменения объема, определенного критического значения, являющегося в свою очередь линейной функцией шарового тензора:

σ_i²=А+Вσ₀+Сσ₀².

Коэффициенты А, В, С определяются из опытов на растяжение, сжатие и кручение:

σ₁²+σ₂²+σ₃²-2( -1)(σ₁σ₂+σ₂σ₃+σ₁σ₃)+(σ_с–σ_р)(σ₁+σ₂+σ₃)=σ_р+σ_с. (2.5.2.4)

При поверхность вращения – сфера;

при - эллипсоид;

при - параболоид;

при - двуполый гиперболоид;

при – круговой конус;

при - однополый гиперболоид;

при σ_р=σ_с, τ_к= и условие (2.5.2.4) превращается в (2.4.6).

2.5.2.3. Баландин П.П. предположил, что предельное значение удельной потенциальной энергии формоизменения является линейной функцией шарового тензора:

σ_i²=А+Вσ₀;

σ₁²+σ₂²+σ₃²-(σ₁σ₂+σ₂σ₃+σ₁σ₃)+(σ_с–σ_р)(σ₁+σ₂+σ₃)=σ_р+σ_с. (2.5.2.5)

В пространстве σ₁, σ₂, σ₃ теория Баландина интерпретируется параболоидом вращения и является частным случаем гипотезы Бушинского. Критерий нашел экспериментальное подтверждение для некоторых бетонов, закаленной стали.

Рисунок 2.5.2.2 - Предельная поверхность – параболоид вращения

2.5.2.4 С гипотезой Бушинского тождественно совпадает теория прочности Ю.И.Ягна, хотя она базируется на совершенно других представлениях. Критерий имеет вид:

(σ₁²+σ₂²+σ₃²)–а(σ₁σ₂+σ₂σ₃+σ₁σ₃)+в(σ₁+σ₂+σ₃)=с;

(σ₁-σ₂)²+(σ₂-σ₃)²+(σ₃-σ₁)²+ (σ₁+σ₂+σ₃)²+ ×

×(σ₁+σ₂+σ₃)=6τ_к². (2.5.2.6)

2.5.2.5 По Миролюбову Н.Н. критерий прочности определяется квадратичной функцией главного тензора напряжений с тремя параметрами, но последние связаны между собой:

(σ_р+σ_с) +(σ_р-σ_с)(σ₁+σ₂+σ₃)=2σ_рσ_с. (2.5.2.7)

Геометрически – это однополостной гиперболоид вращения, следовательно, находится в противоречии с постулатом Друккера: поверхность должна быть выпуклой. Для чугунов при некоторых видах НДС критерий Миролюбова дает хорошие результаты.

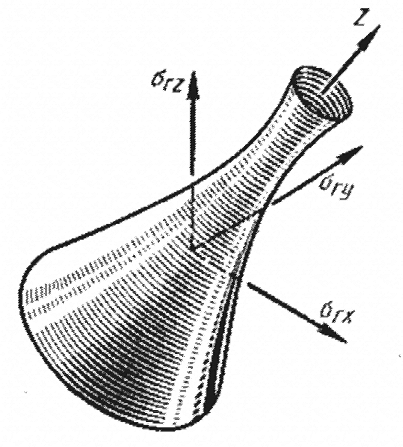
Рисунок 2.5.2.3 - Предельная поверхность – однополостной гиперболоид вращения

2.5.2.6 По Боткину А.И.:

τ_окт=m(n-σ_окт),

. (2.5.2.8)

Уравнение (2.5.2.8) является уравнением кругового конуса (см. рисунок 2.5.2.4), ось которого равнонаклонена к осям σ₁, σ₂, σ₃, а вершина имеет координаты:

σ₁=σ₂=σ₃= .

Рисунок 2.5.2.4 – Предельная поверхность в пространстве напряжений (а), предельная кривая на плоскости напряжений (б)

При σ₃=0 предельная кривая в системе координат σ₁-σ₂ эллипс (1≥ ≥0,27), парабола ( =0,27), гипербола ( ≤0,27).

2.5.2.7. Шкабрелис К.К. предлагает зависимость:

τ_окт^α+аσ_окт^β≤в. (2.5.2.9)

По исследованию материалов типа бетона при плоском напряженном состоянии зависимость (2.5.2.9) принята линейной:

τ_окт+аσ_окт ≤в.

При объемном напряженном состоянии:

≤в, α=1,4….1,6.

2.5.2.8 Друккер и Прагер предложили условие:

τ_окт=(а-вσ_окт)². (2.5.2.10)

2.5.2.9 Гольденблат И.И. и Копнов В.А. предлагают следующий вид:

А(σ₁+σ₂+σ₃)+[B(σ₁²+σ₂²+σ₃²)+C(σ₁+σ₂+σ₃)²]^1/2=1;

(σ₁+σ₂+σ₃)+{ +[ ]×

×(σ₁+σ₂+σ₃)²}^1/2=1. (2.5.2.11)

2.5.2.10 Критерии прочности, интерпретирующиеся поверхностями вращения, были получены также на основе предпосылок, не связанных с энергетическими представлениями.

Дощинский Г.А. считает, что наступление предельного состояния материала определяется величиной абсолютных значений компонентов деформаций. Общей мерой этой величины может служить среднее квадратичное от ε₁, ε₂ и ε₃:

ε_ср^кв= .

Соответствующее этому критерию условие эквивалентности в напряжениях имеет вид:

σ₁²+σ₂²+σ₃²– (σ₁σ₂+σ₂σ₃+σ₁σ₃)=σ_р². (2.5.2.12)

В пространстве напряжений уравнение (2.5.2.12) представляется вытянутым в направлении оси симметрии пространства эллипсоидом вращения, вырождающимся при μ=0,5 в цилиндр Губера-Мизеса-Генки. Для хрупких материалов Дощинский принимает

ε_ср^кв=Аθ+В.

Тогда

(2.5.2.13)

В зависимости от соотношений между константами μ, σ_с, σ_р возможными предельными поверхностями будут цилиндр, конус (при μ=0,5), эллипсоид, параболоид, гиперболоид (при μ≠0,5).

Седоков Л.М. строит критерий прочности для плоского напряженного состояния из следующих соображений.

Через четыре точки [(σ_р, 0), (0, σ_р), (-σ_с, 0), (0, -σ_с)] согласно классической теории прочности проходит эллипс. Но через них можно провести бесчисленное количество других эллипсов:

σ₁²+σ₂²+Сσ₁σ₂=σ_р², где С=2–(σ_р/τ_к)².

Так как по II теории прочности σ_р/τ_к=3/2, то

σ₁²+σ₂²-0,25σ₁σ₂=σ_р².

Аналогично можно построить эллипсы по I и II теориям.

Переход к хрупким материалам можно осуществить, используя безразмерные параметры и переменный масштаб:

, где k, m=1, 2, 3, но k≠m.

При σ_k>0 и σ_m>0, =σ_k,m/σ_р;

при σ_k <0 и σ_m<0, =σ_k,m/σ_с.

Возвращаясь к обычным координатам, можно записать часть контура прочности хрупких материалов, в основе которого лежит уточненная теория наибольших удлинений:

σ₁²+χ²σ₃²-0,25σ₁σ₃=σ_р², (2.5.2.14)

где

или критерий ТПИ (Томский политехнический институт).