2.5 Новые теории прочности

2.5.1 Теории прочности, интерпретирующиеся многогранниками

2.5.1.1 Новый вариант I теории для материалов, по-разному сопротивляющихся растяжению и сжатию (σ_р≠σ_с), интерпретируется кубом, ребро которого равно сумме пределов прочности на растяжение и на сжатие, и начало координат расположено на расстоянии σ_р от граней куба (см. рисунок 2.5.1.1).

Рисунок 2.5.1.1 – Контур предельных состояний по новому варианту I теории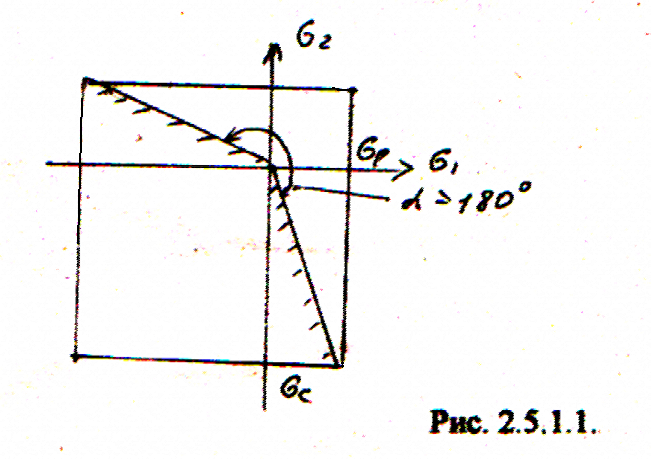

Угол α объединяет все напряженные состояния, ограничением для которых является предел прочности на растяжение (α>180).

2.5.1.2 Седоков Л.М. распространил II уточненную теорию на материалы, у которых σ_р≠σ_с (см. рисунок 2.5.1.2)

Рисунок 2.5.1.2 – Контур предельных состояний по II уточненной теории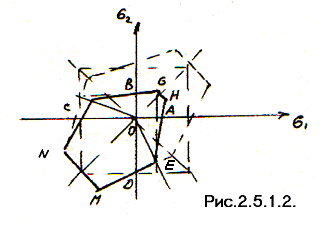

Сингулярный контур прочности, при плоском напряженном состоянии, определяется шестью уравнениями:

σ₁+σ₃=2σ_р;

2σ₁-х²σ₃=2σ_р;

2σ₃-х²σ₁=2σ_р;

σ₁+σ₃=-2σ_с;

2σ₁-σ₃=-2σ_с;

2σ₃-σ₁=2σ_р.

Принято, что точка Е является местом пересечения прямых ДЕ и ОЕ. Уравнение прямой ДЕ:

2σ₃-σ₁=-2σ_с.

Уравнение луча ОЕ, как и для нового варианта I теории:

σ₁=-χσ₃,

где χ=σ_р/σ_с.

Координаты точки Е найдем, решая эти два уравнения:

; .

Тогда уравнение прямой АЕ:

σ₁=σ_р+аσ₃, или σ₁- σ₃=σ_р,

где . (2.5.1.1)

2.5.1.3 Чтобы распространить теорию максимальных касательных напряжений на материалы, по-разному сопротивляющиеся растяжению и сжатию, Кулон предположил, что в случае сжатия максимальное касательное напряжение является линейной функцией нормального напряжения σ^′ в плоскости расположения τ_max:

τ_max=аσ^′+в.

Для растяжения и сжатия:

; ;

Учитывая, что τ_max=(σ₁-σ₃)/2 и σ^′=(σ₁+σ₃)/2, получаем:

σ₁- σ₃=σ_р

или

σ₁-χσ₃=σ_р. (2.5.1.2)

Предельная поверхность, соответствующая условию (2.5.1.2) – шестигранная равнонаклоненная к осям пирамида (см. рисунок 2.5.1.3).

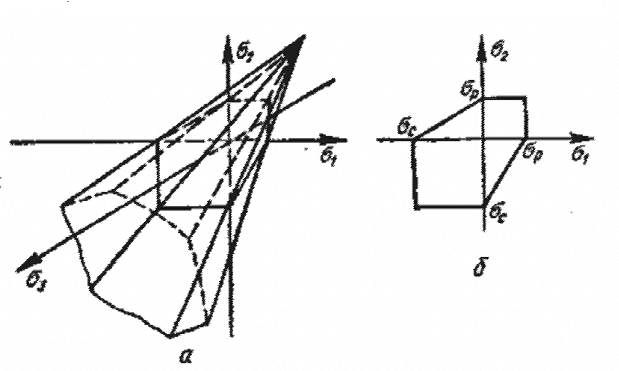
Рисунок 2.5.1.3 – Предельная поверхность в пространстве напряжений (а) и предельная кривая на плоскости напряжений (б)

К уравнению (2.5.1.2) приводит также теория прочности Мора, если предположить, что предельная кривая, огибающая круги напряжений – прямая линия (см. рисунок 2.5.1.4).

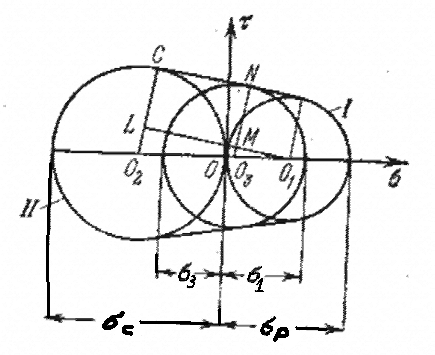
Рисунок 2.5.1.4 – Предельная кривая по теории прочности Мора

Если CN – прямая, то

или .

Тогда

; σ₁-χσ₃=σ_p.

Основной смысл теории Мора сводится к эмпирическому определению кривой τ=f(σ), огибающей семейство предельных главных кругов Мора и состоящей из двух симметричных ветвей. Абсциссы σ и ординаты τ точек касания кругов огибающими представляют нормальные и касательные напряжения, при которых начинается пластический сдвиг или разрушение. Таким образом, физический смысл теории Мора можно сформулировать так: нарушение прочности материала наступает либо при достижении касательными напряжениями τ некоторой критической величины, зависящей от нормальных напряжений σ, действующих по тем же плоскостям скольжения, либо при достижении наибольшим нормальным напряжением σ₁ предельного для данного материала значения.

Теория Мора продолжает совершенствоваться.

Прандтль предложил условие:

σ₁-σ₃=С₁-С₂(σ₁+σ₃),

которое приводит к условию (2.5.1.2). Основной недостаток условия (2.5.1.2) – неучет влияния напряжения σ₂.

2.5.1.4 Другие теории прочности, выражаемые линейными функциями с использованием двух констант и учитывающие влияние напряжений σ₂.

2.5.1.4.1 Седоков Л.М. сделал предположение о том, что максимальное касательное напряжение при разрушении линейно зависит от гидростатического давления:

τ_max=аσ_о+в.

После определения коэффициентов а и в при простейших нагружениях, получим:

σ₁-χσ₃+½(1-χ)σ₂=σ_р (2.5.1.3)

При σ₂=0 условия (2.5.1.2) и (2.5.1.3) совпадают.

2.5.1.4.2 Тарасенко И.И. предположил следующее условие:

σ₁+кσ_о=m.

Отсюда:

σ₁–χ(σ₂+σ₃)=σ_р. (2.5.1.4)

При σ₂=0 условия (2.5.1.2) и (2.5.1.4) совпадают.

2.5.1.4.3 Максимальная деформация сдвига при разрушении по Занделю линейно зависит от средней величины главных удлинений:

γ_мах=а-в(ε₁+ε₂+ε₃).

Отсюда: σ₁+½(1-х)σ₂-хσ₃=σ_р (2.5.1.5)

При σ₂=0 условия (2.5.1.2) и (2.5.1.5) совпадают. В пространстве напряжений условие (2.5.1.5) соответствует поверхности шестигранной пирамиды, вписанной в конус.

2.5.1.5 В.Киссель и Ф.Блюм построили теорию прочности в следующей форме:

σ_р=Аσ₁+Вσ₂+Сσ₃+Д│σ₁│+Е│σ₂│+F│σ₃│.

Предположив отсутствие влияния σ₂=0, получили:

. (2.5.1.6)

2.5.1.6 А.Ф.Липатов предложил гипотезу, основанную на учете изменчивости хрупко-пластических свойств материала в зависимости от шарового тензора: с увеличением всестороннего сжатия хрупкий материал приобретает пластические свойства и, начиная с определенной величины гидростатического давления, ведет себя как пластическое тело, разрушаясь при значительных деформациях. В условиях всестороннего растяжения такой пластичный материал разрушается хрупко, при этом деформации формоизменения практически отсутствуют.

Липатов ввел уравнение:

σ₁²+2σ_плσ₁+σ_с²=σ₃²,

где σ_пл – предел текучести в идеально пластическом состоянии.

Предел текучести находится из условия одноосного растяжения:

.

Тогда σ₁²- σ₁+σ_с²=σ₃². (2.5.1.7)

Если σ_р=σ_с условие (2.5.1.7) переходит в (2.5.1.2).

Предельная поверхность критерия Липатова представляет собой равнонаклоненную к осям пространственную фигуру, имеющую в нормальном сечении правильный шестиугольник, размеры которого увеличиваются с увеличением гидростатического сжатия. При этом стороны шестиугольника асимптотически приближаются к граням призмы Кулона.