2.4.3 Теория наибольших касательных напряжений (III теория, теория Кулона)
Любые напряженные состояния материала будут равнопрочными, если у них максимальные касательные напряжения равны:
σс≤σ1–σ3≤σр. (2.4.5)
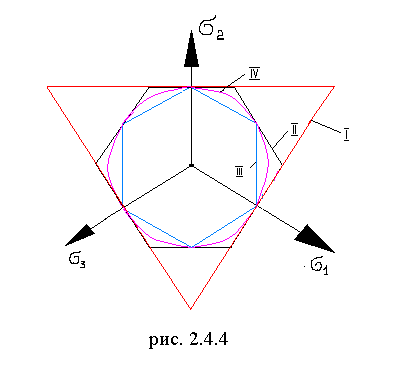
Соответствующие соотношениям (2.4.5) шесть плоскостей при пересечении образуют правильную шестигранную призму.
Как показали опыты для пластических материалов, эта теория прочности дает удовлетворительные результаты, но плохо согласуется с экспериментальными результатами для хрупких материалов.
2.4.4 Энергетическая теория прочности (IV теория, теория Губера, Мизеса, Генки)
Любые напряженные состояния материала будут равнопрочными, если у них удельные потенциальные энергии формоизменения равны.
. (2.4.6)
Уравнение (2.4.6) в пространстве напряжений σ1, σ2, σ3 определяет поверхность равнонаклоненного к осям кругового цилиндра, описанного вокруг призмы Кулона. При плоском напряженном состоянии предельная кривая представляет эллипс. Эта теория хорошо оценивает поведение пластических материалов. Но плохо – хрупких.
2.4.5 Сопоставление классических теорий прочности при плоском напряженном состоянии
На рисунке 2.4.2 дано сопоставление контуров предельных состояний по классическим теориям прочности.
Рисунок 2.4.2 – Контуры предельных
состояний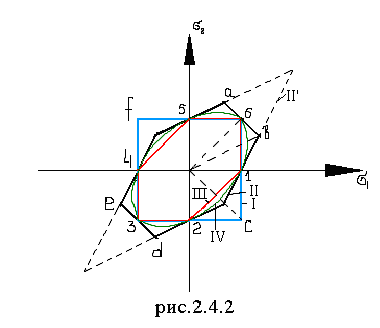
I – первая теория прочности, II – вторая теория прочности (уточненная),
II' – вторая теория прочности (классическая), III – третья теория прочности,
IV – четвертая теория прочности.
Все четыре теории прочности имеют шесть общих точек 1,…,6. Эквивалентные напряжения в этих точках по всем четырем теориям прочности близки. Наибольшие расхождения в точках: a, b, c, d, e, f.Соотношения между пределами прочности на сдвиг и растяжение, рассчитанные по теориям, соответственно равны:
;
2/3; 1/2; 1/
.
Чтобы быстро сопоставить значения эквивалентных напряжений, можно использовать графический способ (см. рисунок 2.4.3).
σ3 σ1
A
D
σ2
H O B
Е
M
С
Рисунок 2.4.3 – Графический способ сравнения эквивалентных напряжений
ABC – равносторонний треугольник; OB=σэквI (по построению); CE=σэквII (надо доказать); AC=σэквIII (по построению); CD=σэквIV (надо доказать).
CD=
;
CH2=[(σ1−σ3)cos30˚]2=
(σ1–σ3)2;
HD2=[
]2=(
)2;
CD=
=
,
что и требовалось доказать.
CE=CM+ME=CHcos30˚+HDsin30˚=
(σ1–σ3)+
=σ1–
(σ2+σ3)=σэквII,
что и требовалось доказать.
Из рисунка 2.4.3 видно:
а) если σ2 по знаку и величине близко к σ1 или к σ3, то значения эквивалентных напряжений, рассчитанные по второй, третьей и четвертой теориям прочности, будут близки друг к другу AC≈DC≈EC;
б) если
σ2=
,
то значения эквивалентных напряжений, посчитанные по второй, третьей и четвертой теориям прочности, будут иметь наибольшее расхождение:
AC:DC:CE=1:
:
;
в) при трехосном растяжении и сжатии расчетное значение эквивалентных напряжений по теории наибольших нормальных напряжений существенно отличается от соответствующих значений по другим классическим теориям прочности и противоречит фактическим результатам.
На рисунке 2.4.4 показано девиаторное сечение поверхностей предельной прочности по I, II, III и IV классическим теориям.
Рисунок 2.4.4 - Девиаторные сечения
поверхностей прочности