2.2.4 Упругая энергия и работа пластической деформации

В упругих телах работа внутренних сил упругости превращается в потенциальную энергию и численно равна ей:

, (2.2.4.1)

или

, (2.2.4.2)

или

, (2.2.4.3)

или

. (2.2.4.4)

Полную удельную (накапливаемую в единице объема) потенциальную энергию можно разбить на упругую энергию изменения формы

(2.2.4.5)

и упругую энергию изменения объема

. (2.2.4.6)

Другая запись:

; (2.2.4.7)

. (2.2.4.8)

Важнейший вывод об энергетической интерпретации второго инварианта девиатора напряжений: с точностью до постоянного множителя 2G второй инвариант девиатора напряжений представляет собой удельную потенциальную энергию формоизменения.

Удельная работа пластического деформирования при σ_i =Ф(ε_i)

. (2.2.4.9)

2.3 Условия прочности. Предельные поверхности

Расчеты на прочность в традиционной постановке проводятся по схеме: определение НДС, сравнение в каждой точке с предельным состоянием (разрушение или возникновение текучести), оценка коэффициентов запаса. НДС считается известным, если определены в каждой точке тензоры напряжений и деформаций, для чего используются расчетные и экспериментальные методы.

2.4 Классические теории прочности Классические теории прочности относятся только к изотропным средам с одинаковыми пределами прочности на растяжение и сжатие:

σ_р=σ_с.

2.4.1 Теория наибольших нормальных напряжений (I теория)

Любые напряженные состояния данного материала будут равнопрочными, если у них наибольшие нормальные напряжения равны. Следовательно,

σ_р≤σ₁≤σ_с (2.4.1)

при условии σ₁>σ₂>σ₃,

где σ_р, σ_с - предельные напряжения при растяжении и сжатии (предел текучести, предел прочности или допускаемые напряжения).

Соотношение (2.4.1)определяет в пространстве напряжений шесть плоскостей, параллельных координатным осям. Пересекаясь, эти плоскости образуют куб, на поверхности которого лежат точки, соответствующие предельным состояниям материала. На плоскости область безопасных напряженных состояний ограничена квадратом. Эта теория плохо соответствует данным испытаний многих реальных материалов. Она не объясняет, например, практически неограниченную прочность при высоких гидростатических давлениях.

2.4.2 Теория наибольших относительных удлинений (II теория)

Любые напряженные состояния материала будут равнопрочными, если у них наибольшие относительные удлинения равны:

ε_с≤ε₁≤ε_р, при условии ε₁>ε₂>ε₃,

или

σ_с≤σ₁−μ(σ₂+σ₃)≤σ_р, (2.4.2)

при условии σ₁>σ₂>σ₃.

Выражение σ₁−μ(σ₂−σ₃) еще называют эквивалентными напряжениями σ_экв.

Соотношение (2.4.2) в пространстве напряжений интерпретируется трехгранной призмой, а с учетом поправки Грасгофа – шестью парами плоскостей, которые, пересекаясь, образуют равносторонний косоугольный параллелепипед (ромбоид) с осью симметрии, равно наклоненной к координатным осям.

Для плоского напряженного состояния II теория интерпретируется ромбом (Мариотт, Сен-Венан, Г.Н.Кузнецов), треугольниками (Н.М.Беляев, М.М.Филоненко-Бородич).

Л.М.Седоков провел уточнение II теории. Аналогичные уравнения получены Ишлинским А.Ю. Он предлагает рассматривать 3 уравнения:

σ₁−μ(σ₂+σ₃)= σ_р;

σ₂−μ(σ₃+σ₁)= σ_р;

σ₃−μ(σ₁+σ₂)= σ_р

или

│σ_k−μ(σ_l+σ_m)│_max=σ_р,

где k, l, m =1, 2, 3 и заменяются круговой подстановкой, но k≠1≠m.

Для правильности расчета из шести значений эквивалентных напряжений нужно выбрать численно наибольшее значение. Так как μ – изменяется при нагружении, то предлагается μ=0,5, значение в момент разрушения.

Тогда

│σ_k−(σ_l+σ_m)/2│_max=σ_р. (2.4.3)

Границы контура прочности при плоском напряженном состоянии для идеально-пластического материала, одинаково работающего на растяжение и сжатие, определяются шестью уравнениями:

2 ₁– ₂=2; 2 ₁– ₂=-2;

2 ₂– ₁=2; 2 ₂– ₁=-2; (2.4.4)

₁+ ₂=2; ₁+ ₂=-2.

Здесь ₁ и ₂ безразмерные координаты: ₁=σ₁/σ_р, ₂=σ₂/σ_р.

Рисунок 2.4.2 - Контуры предельных состояний по второй теории прочности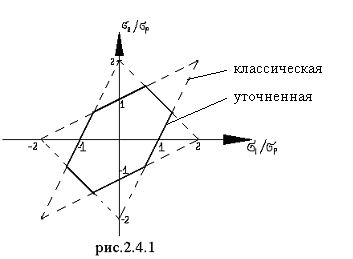

Таким образом, при равном двухосном растяжении прочность не выше, чем при простом растяжении.