1. Якщо вчитель паралельно креслив схему повного аналізу, то : кінцевий вигляд такий:

   

   12 ■3 = 36 (км);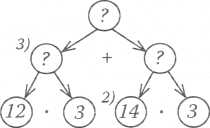

2. 14 ■3 = 42 (км);

3. 36 + 42 = 78 (км).

Вираз: 12 -3 + 14 • 3 = 78 (км).

Як видно з виразу, розв’язання є сумою двох добутків. У кож ному добутку другий множник - однаковий. Це наводить на др} гий спосіб розв’язання:

(12 + 14) ■3 = 78 (км).

Що означає у цьому виразі сума швидкостей 12 + 14? Вона ма назву “швидкість зближення” велосипедистів і показує, на скіль ки кілометрів зближуються велосипедисти через кожну ГОДИН} Щоб учні осмислили другий спосіб розв’язування, їм потрібно де кладно пояснити, що таке швидкість зближення. Це можна зроби ти на тому самому кресленні, за яким пояснювався перший епосі розв’язування. Учитель правою і лівою рукою показує почато: руху велосипедистів - крайні точки відрізка.

- Де перебуватимуть велосипедисти через 1 год? (Учитель збль жує руки на одну поділку з кожного боку.) Скільки пройшов пер ший велосипедист за 1 год? (12 км.) Другий? (14 км.) На скільк: кілометрів вони зблизилися за 1 годину? (На 12 + 14 = 26 км.) Бон: зблизилися на 26 км за годину - це швидкість зближення. НІвца кість зближення у даному разі дорівнює сумі обох швидкостей. Д перебуватимуть велосипедисти ще через годину? (Учитель показу на кресленні.) На скільки кілометрів зблизилися велосипедист: протягом другої години? (Знову на 26 км.) Де перебуватимуть вє лосипедисти після третьої години руху? (Вони зустрінуться.) Н скільки кілометрів зблизилися велосипедисти протягом третьої гс

дини? (Ще раз на 26 км.) Ви бачите, що через 3 год велосипедисти разом пройшли всю відстань між містами - кожний свою частину. А як вони рухалися? (Щогодини вони зближувалися на 26 км. Так тривало 3 год.) Як можна знайти всю відстань, яку вони проїхали разом? (26 • 3.) Так, швидкість зближення помножимо на час збли­ження і дістанемо всю відстань між містами.

Розв’язання:

1. 12 + 14 = 26 (км/год) - швидкість зближення велосипедистів;

2. 26 ■ 3 = 78 (км) - відстань між містами.

Задачу на знаходження однієї із швидкостей можна скласти як обернену до щойно розглянутої.

З двох міст, відстань між якими 78 км, одночасно виїхали на­зустріч один одному два велосипедисти і зустрілися через 3 год. Швидкість першого велосипедиста 12 км/год. Яка швидкість другого велосипедиста?

12 км/год

? км/год < г-

З год

78 км

Нам наперед відома друга швидкість - 14 км/год. Тому на кресленні вчитель справа відкладає довші відрізки, ніж зліва. Але щоб правильно зобразити креслення до наступних задач на знаходження швидкості, вчитель повинен заздалегідь розв’язати таку задачу: знайти невідому швидкість і порівняти її з даною швидкістю. Лише після цього він знатиме, які відрізки треба від­кладати на малюнку.

Ці нюанси повинні розуміти учні: чим менша швидкість, тим менші відрізки. Прапорець, що позначає місце зустрічі, у біль­шості задач не можна зображувати точно посередині відрізка, як це часто роблять учні. Якщо він посередині, то це означає, що обидва учасники руху їхали з однаковою швидкістю і до зустрічі кожний проїхав половину всієї відстані. Якщо ж швидкості їхні різні, то більшу відстань до зустрічі проїде той учасник, швид­кість якого більша.

Задача, у якій невідомою є одна зі швидкостей, також розв’язується двома способами. Перший ґрунтується на розгляді суми відстаней, а другий — суми швидкостей.

1. спосіб.

1. 12 ■ 3 = 36 (км) - проїхав перший велосипедист до зустрічі;

2. 78-36 = 42 (км) - проїхав другий велосипедист до зустрічі;

3. 42 : 3 = 14 (км/год) - швидкість другого велосипедиста.

Вираз: (78 - 12 ■ 3) : 3 = 14 (км/год).

При складанні виразу учні стежать, щоб усі числа, які входя¹ до виразу, були дані в умові задачі. Цей вираз є досить складни: тому його варто складати вже після розв’язання задачі діям: Можна вчити послідовно використовувати результати кожної ді починаючи з останньої:

42 : 3 = 14 (км/год).

Але числа 42 немає в умові; це результат другої дії. Тому пі, ставимо замість нього вираз 78 - 36:

(78 -36): 3 = 14 (км/год).

Але числа 36 також немає в умові, замість нього ми підставі мо з першої дії вираз 12-3:

(78 - 12 ■ 3) : 3 = 14 (км/год).

2. спосіб.

Учням треба пояснити, що якщо всю відстань 78 км поділит: на час 3 год, то дістанемо число 26 км - суму відстаней, на як зближаються велосипедисти за 1 год, тобто швидкість зближення Швидкість зближення - це сума двох швидкостей. Перша швид кість відома, то другу знайдемо дією віднімання.

1. 78 : 3 = 26 (км/год) - швидкість зближення велосипедистів;

2. 26-12= 14 (км/год) - швидкість другого велосипедиста.

Вираз: 78 : 3 - 12= 14 (км/год).

Третя обернена задача передбачає знаходження часу руху де зустрічі. Її особливістю є те, що вона розв’язується лише способом на дві дії - через швидкість зближення.

З двох міст, відстань між якими 78 км, одночасно виїхали на­зустріч один одному два велосипедисти. Швидкість першого велосипедиста 12 км/год, а другого - 14 км/год. Через скільки годин вони зустрілися?

12 км/гдЬ _{? го}^ ^14 км/год

78 км

- Якщо обидві швидкості відомі, то що можна взнати? (Швид­кість зближення. 12 + 14 = 26 (км/год).) Що означає 26 км/год? (Це означає, що за першу годину вони зблизилися на 26 км, за другу - знову на 26 км і так до тих пір, поки не зустрілися.) А коли зустрінуться, то яку відстань вони разом пройдуть? (Усю відстань між містами - 78 км.) Отже, скільки годин триватиме процес зближення? /Стільки, скільки разів по 26 км вміститься у 78 км.) То яка буде друга дія? (78 : 26 = 3 (год).)

Вираз: 78 : (12 + 14) = 3 (год).

Ви, мабуть, помітили, що у розборах задач на зустрічний рух, які розв’язуються двома діями, ми відходимо від домовленості не обчислювати під час розбору. Так варто чинити в усіх складних розборах. Якщо учням важко уявити собі структуру розв’язання в абстрактній формі, то доцільно розбір наповнити конкретними обчисленнями. А в даному разі розв’язання двома діями хоч і ко­ротке, проте важке.

У підручнику на основі задачі на знаходження часу є розширена задача (№ 852). У ній швидкості невідомі, однак їх можна знайти.

З двох міст, відстань між якими 900 км, одночасно назустріч А' один одному вирушили два автомобілі. Перший автомобіль усю відстань проїхав за 15 год, а другий -за 10год. Через скільки го­дин після виїзду автомобілі зустрілися?

-

Нам довелося змінити обраний нами сюжет, щоб ділення мож­на було виконати націло. Щоб точніше виконати креслення, учи­тель наперед обчислює швидкості.

Ця задача корисна тим, що, порівняно з попередньою, учні ще раз можуть осмислити той факт, що дії можна виконувати лише над відповідними значеннями величин. Щоб знайти швидкість першо­го автомобіля, потрібно відстань, яку проїхав перший автомобіль, поділити на час, протягом якого він її подолав. Але в контексті нашої задачі можна говорити про дві відстані, які проїжджав пер­ший автомобіль: 1) він проїхав відстань до зустрічі; 2) він проїхав усю відстань між містами. Яка ж з цих відстаней відповідає часу 15 год? Уся відстань 900 км, а не відстань до зустрічі. Аналогічні

міркування необхідно здійснити і про другий автомобіль. Нелегко усі ці відповідності зобразити на кресленні. Адже над прапорцем - місцем зустрічі - прийнято записувати час руху до зустрічі — він однаковий для обох учасників руху. А час проходження всієї від­стані - різний (15 год і 10 год), бо автомобілі їдуть з різними швидкостями, а проїжджають ту саму відстань між містами.

Креслення може бути таким:

? км/год

через 10 год

? км/год ■< 1—діерез 15 год

? год

900 км

Нам невідомо, скільки годин їхали автомобілі до зустрічі, тому на кресленні ми не можемо позначити поділки. Швидкості теж невідомі, проте видно, що перший автомобіль їхав довше, отже, його швидкість і відстань до зустрічі - менші.

• Якщо перший автомобіль усю відстань 900 км проїхав за 15 год, про що можна дізнатися? (Про швидкість першого авто­мобіля.) У разі потреби, її можна відразу обчислити:

1. 900 : 15 = 60 (км/год).

• Якщо другий автомобіль усю відстань проїхав за 10 год, то про що можна дізнатися? (Про швидкість другого автомобіля.)

2. 900 : 10=90 (км/год).

Учитель замість знаків питання наносить на креслення знай­дені швидкості, і учні впізнають знайомий вид задачі. Наступні дії не викликатимуть труднощів, якщо попередню задачу на зна­ходження часу зближення учні засвоїли:

3. 60+90= 150 (км/год) - швидкість зближення;

4. 900 ■ 150 = 6 (год) - час руху до зустрічі.

Задачі на рух з однієї точки у протилежних напрямах мають таке саме розв’язання, як і відповідні задачі на зустрічний рух.

Розглянемо їх, використавши обраний раніше сюжет про ве­лосипедистів.

З однієї автостоянки у протилежних напрямах одночасно ви­рушили два велосипедисти. Перший велосипедист їхав зі швид­кістю 12 км/год, а другий - 14 км/год. Яка відстань буде між ними через 3 год?

14 км/год 12 км/год

Ч

Через 3 год - ? км

1. спосіб.

1. 12 • 3 = 36 (км) - проїхав за 3 год перший велосипедист;

2. 14 • 3 = 42 (км) - проїхав за 3 год другий велосипедист;

3. 36 + 42 = 78 (км) - відстань між велосипедистами через 3 год.

2. спосіб.

1. 12 + 14 = 26 (км/год) - швидкість віддалення велосипедистів;

2. 26 • 3 = 78 (км) - відстань між велосипедистами через 3 год.

Відмінність між задачами на зустрічний рух і рух у різні сторо­ни полягає в тому, що сума швидкостей тут називається швидкістю віддалення, бо показує, на скільки кілометрів за 1 год віддаляються велосипедисти. Як і у відповідній задачі на зустрічний рух, швид­кість віддалення треба дуже докладно пояснити на кресленні.

Обов’язково треба провести роботу на порівняння розв’язань обох задач. Проте вони розглядаються не на одному уроці. Тому можна провести творчу роботу над уже розв’язаною задачею на рух у проти­лежних напрямах — перетворити її у задачу на зустрічний рух:

- Уявіть собі, що, проїхавши 3 год, велосипедисти одночасно зупинилися і повернули назад. Яку задачу можна скласти? Яке її розв’язання? (Таке саме.)

Підручник пропонує розширені задачі на рух у протилежних напрямах, де одна зі швидкостей задана різницевим відношенням до другої.

З однієї автостоянки одночасно у протилежних напрямах ви­їхали два велосипедисти. Швидкість першого велосипедиста 12 км/год, а другого - на 2 км/год більша, ніж першого. Через скільки годин відстань між велосипедистами буде становити 78 км?

Необхідно звернути увагу, що й у випадку руху з однієї точ­ки у протилежних напрямках задача, у якій потрібно знайти час, розв’язується лише одним способом — через швидкість віддалення:

1. 12 + 2 = 14 (км/год) - швидкість другого велосипедиста;

2. 12 + 14 = 26 (км/год) - швидкість віддалення велосипедистів;

3. 78 ■ 26 = 3 (год) - час віддалення велосипедистів на 78 км.

Задачі на рух в одному напрямі також поділяються на дв види: 1) коли учасники вирушили одночасно з однієї точки

2. коли один учасник наздоганяє другого. У першому випадку першої ж миті учасник, що рухається швидше, почне віддалятись від другого. Тому тут ми оперуємо швидкістю віддалення, але прі русі в одному напрямі швидкість віддалення дорівнює не сумі, і різниці швидкостей.

Якщо за 1 год перший велосипедист проїхав 12 км, а другий - з тієї самої точки у тому самому напрямі - 14 км, то за цю годищ другий випередив першого на14-12 = 2 км.

12 км/год

' '2 км/год - швидкість віддалення

14 км/год

У другому випадку, коли один рухомий об’єкт наздоганяє ін­шого, різниця швидкостей називається швидкістю зближення, бс другий велосипедист наздоганяє першого і вони зближуються, за кожну годину відстань між ними скорочується на 2 км. У підруч­нику є лише дві задачі на рух в одному напрямі (№№ 444, 693), тому ми не будемо розглядати усіх взаємообернених задач на рух в одному напрямі (а їх є стільки ж, скільки і задач на рух у проти­лежних напрямах - по 3 на кожний випадок руху). Обмежимося лише випадками, що їх містить підручник.

Задача на рух з однієї точки

1. З одного подвір’я в одному напрямі одночасно вирушили два ве­лосипедисти зі швидкостями відповідно 12 км/год і 14 км/год.

Яка відстань буде між ними через 3 год?

Оскільки обидва велосипедисти їдуть по одному і тому ж відрізку дороги, для зручності розведемо їхні шляхи на два пара­лельних відрізки:

12 км/год _3год

^ '! . ^
14 км/год_		3 год Р-
□

? км

Учитель докладно пояснює на кресленні, як рухався кожний велосипедист.

Спроектувавши місцезнаходження першого велосипедиста че­рез 3 год на маршрут другого, дістанемо наочне зображення того, на скільки він відстав за 3 год від другого.

1. спосіб.

1. 12 • 3-36 (км) - проїхав за 3 год перший велосипедист;

2. 14 • 3 = 42 (км) - проїхав за 3 год другий велосипедист;

3. 42 - 36 = 6 (км) - на стільки другий велосипедист випередив першого.

Відповідь: через 3 год відстань між велосипедистами станови­тиме 6 км.

Вираз: 14 • 3 - 12 ■ 3 = 6 (км).

2. спосіб.

Учитель на кресленні показує, на скільки випередив другий ве­лосипедист першого через 1 год - на 2 км, бо14-12 = 2 (км/год) - швидкість віддалення велосипедистів. Протягом другої години другий велосипедист випередить першого ще на 2 км, і відстань між ними становитиме вже 2 + 2 = 4 (км). Протягом третьої го­дини відстань між ними збільшиться ще на 2 км і становитиме: 2 + 2 + 2 = 6 (км). Тому розв’язання другим способом має вигляд:

1. 14 - 12 = 2 (км/год);

2. 2- 3 = 6 (км).

Складність цієї задачі полягає в тому, що обидва велосипедис­ти переміщаються і відстань між ними одночасно і зростає, і пе­реміщається разом з велосипедистами. Доцільно цей рух показати наочно, фіксуючи відстань через кожну годину.

2. Задача на рух в одному напрямі, коли один рухомий об’єкт наздоганяє іншого.

Від Луганська до Львова летіли літак і вертоліт. Спочатку літак був позаду вертольота на 400 км. Швидкість літака 12 км/хв, а вертольота - 2 км/хв. Яка буде між ними відстань через 20 хв? Коли літак порівняється з вертольотом?Яка від­стань буде між ними через 1 год?

12 км/х^ ²™^/хв

_А ' Львів

Луганськ 400 км

І спосіб.

- Подивіться на малюнок і скажіть, який момент польоту на ньому зображено? (Початковий момент, коли між літаком і вер­тольотом відстань становила 400 км.) Щоб дізнатися, яка від-

стань буде між літаком і вертольотом через 20 хв, давайте спочат-

ку визначимо, де опиниться кожен з них через 20 хв. Чи можемо ми дізнатися, скільки кілометрів пролетить літак за 20 хв? (Так. 12-20 = 240 (км).) Вчитель відмічає місцезнаходження літака прапорцем. Про що тепер можна дізнатися? (Скільки кілометрів пролетить вертоліт за 20 хвилин: 2 ■ 20 = 40 (км).)

Вчитель показує і цю відстань на малюнку.

12 км/хв 2 км/хв

Луганськ 400 км

Як можна тепер обчислити відстань між прапорцями? Можна дізнатися, на якій відстані від Луганська буде вертоліт. А на якій відстані від Луганська в цей момент буде літак, ми вже знаємо. То як тоді дізнатися про відстань між літаком і вертольотом? (Від усієї відстані, яку пролетів від Луганська вертоліт, віднімемо відстань, яку пролетів літак.) При цьому вчитель усі відстані показує на малюнку. Після цього учень коментує, а решта учнів записують дії з поясненням:

1. 12 • 20 = 240 (км) - пролетів літак за 20 хв;

2. 2 • 20 = 40 (км) - пролетів вертоліт за 20 хв;

3. 400 + 40= 440 (км) - пролетів усього вертоліт;

4. 440 - 240 = 200 (км) - буде відстань між ними через 20 хв.

Чи можна обчислити цю відстань по-іншому? Погляньте на малюнок і покажіть, з яких двох частин складається відстань між прапорцями. (Один учень показує.) Чи можемо ми обчислити першу частину? (Так, треба від 400 км відняти відстань, яку пролетів літак.) Що зробимо після цього? (До знайденого резуль­тату додамо другу частину - 40 км.)

II спосіб.

1. 12 • 20 = 240 (км) - пролетів літак за 20 хв;

2. 400 - 240 = 160 (км) - не долетів літак до місця, у якому перебу­вав вертоліт у початковий момент;

3. 2 ■ 20 = 40 (км) - пролетів вертоліт за 20 хв;

4. 160 + 40 = 200 (км) - буде відстань між ними через 20 хв.

Ви бачите, що другий спосіб не є коротшим від першого. Але є ще один спосіб. Без обчислення відстаней, які пролетіли літак і вертоліт за 20 хв. Подивіться на їхні швидкості. Як вони опи­сують рух обох літальних апаратів? (Обидва рухаються в одно­му напрямі. Літак летить швидше, отже, наздоганяє вертоліт, тому відстань між ними скорочується.) Отже, найбільша від­стань — 400 км — була між ними у початковий момент, а далі вона почала зменшуватися, тобто літак почав наближатися до вертольо­та. Чи можемо ми дізнатися, на скільки кілометрів наблизиться літак до вертольота за 1 хв? (Так. За 1 хв літак пролетить 12 км.) Якби вертоліт не рухався, це означало б, що літак за 1 хв набли­жається до вертольота на 12 км. Але вертоліт за цю саму хвилину віддаляється від літака на 2 км. Отже, в цілому, літак за хвили­ну наблизиться до вертольота не на 12 км, а на 12 - 2 = 10 (км). Якщо обидва рухаються в одному напрямі 20 хв, на скільки кі­лометрів вони зблизяться через 20 хв? (На 10 • 20 = 200 (км).) Якщо початкова відстань між ними була 400 км, а за 20 хв ця відстань зменшилася на 200 км, то про що можна дізнатися? (Яка відстань стала між літаком і вертольотом через 20 хв.)

Один учень на дошці записує третій спосіб розв’язання, корот­ший за попередні.

III спосіб.

1. 12 - 2 = 10 (км) - на таку відстань наближається літак до вертольота за кожну хвилину;

2. 10 ■ 20 = 200 (км) - на таку відстань наблизиться літак до вертольота через 20 хв;

3. 400 - 200 = 200 (км) - буде відстань між ними через 20 хв.

- Ми відповіли лише на перше запитання. Тепер дізнаємося, коли літак порівняється з вертольотом. Що це означатиме? (Що обидва перебуватимуть на однаковій відстані від Луганська.) Вчитель показує на малюнку цю точку:

12 км/хв 2 км/хв

щ Р- ,

* ' ' Львів

Луганськ 400 км

— Літак порівняється з вертольотом, коли початкова відстань між ними 400 км скоротиться до нуля. За одну хвилину вона ско­рочується на 10 км. То як дізнатися, скільки хвилин триватиме це скорочення? (400 ' 10 = 40 (хв).) Отже, через 40 хв початкова відстань між ними зійде нанівець, тобто літак наздожене вертоліт. Давайте перевіримо, чи дійсно через 40 хв і літак, і вертоліт пе­ребуватимуть на однаковій відстані від Луганська. На якій від­стані від Луганська буде знаходитися літак? (12 • 40 = 480 (км).) А як дізнатися, на якій відстані від Луганська перебуватиме у цей момент вертоліт? (2 ■ 40 = 80 (км) - стільки пролетить вер­толіт за 40 хв; 400 + 80 = 480 (км) - на такій відстані від Луганська перебуватиме вертоліт.) Ви бачите, що відстані від Луганська однакові і у літака, і у вертольота, отже, вони у цей мо­мент перебувають в одній точці траси. Це означає, що через 40 хв літак дійсно порівняється з вертольотом.

Залишилося дати відповідь на останнє запитання: яка відстань буде між ними через 1 год? Цю відстань можна також обчислити довшим і коротшим шляхом. Під керівництвом учителя учні за­писують обидва способи.

І спосіб.

1. 2 ■ 60 = 120 (км) - пролетить вертоліт за 1 год;

2. 400 + 120 = 520 (км) - на стільки відлетить вертоліт від Лу­ганська;

3. 12 ■ 60 = 720 (км) - пролетить літак за 1 год;

4. 720 - 520 = 200 (км) - на стільки літак випередить вертоліт.