Ознайомлення із поняттям “складена задача”

Опрацювання задач на дві дії є початком роботи над складе­мося задачами і тому має винятково важливе значення. Саме тут літи вчаться розбирати задачу від числових даних і від запитання; розв’язувати задачу складанням виразу. Неякісна робота над за­дачами на дві дії призводить до подальшого нерозуміння учнями шлач на 3-4 дії.

Щоб підвести учнів до усвідомлення сутності складеної зада­чі. потрібно показати їм, що бувають задачні ситуації, у яких не зшсди можна відразу знайти відповідь. З цією метою підручник пропонує задачі з недостатніми даними. Розглянемо таку задачу.

Мама принесла з саду жовті і червоні сливи. 4 сливи вона дала дітям. Скільки слив залишилося у мами?

У ході бесіди діти усвідомлюють, що в умові бракує кількості [в, які мама принесла з саду, придумують це число, наприклад 10, і розв’язують задачу. Далі вчитель ускладнює умову:

- Уявіть собі, що в задачі сказано: “Мама принесла 5 жовтих

1. 5 червоних слив”. (А далі той самий зміст.) Як тепер можна розв’язати задачу?

Якщо учні знову називають дію 10 - 6 = 4, учитель запи­тує: звідки взялося число 10, адже його немає в умові? Щоб воно з'явилося, треба спочатку дізнатися, скільки всього слив принесла лама. Учні обчислюють: 5 + 5 = 10. Отже, у першій дії ми дізна­лися, скільки всього слив було у мами, а вже у другій - скільки залишилося. Таким чином, ми вперше зустрілися із задачею, яка розв’язується не однією, а двома діями. Такі задачі називаються складеними, бо вони складаються із кількох простих задач. Да­вайте розіб’ємо нашу задачу на дві прості:

1. Мама принесла із саду 5 жовтих і 5 червоних слив. Скільки всього слив принесла мама?

2. Мама принесла із саду 10 жовтих і червоних слив. 4 сливи вона віддала дітям. Скільки слив залишилося у мами?

Доцільно сформулювати учням ще одну таку пару простих за­дач і запропонувати їм замінити цю пару однією задачею.

Корисно опрацювати з учнями пару задач “проста - складена”, які відрізняються лише запитанням, а умову мають однакову.

1. В одній коробці 6 олівців, а у другій - на 4 олівці більше. Скільки олівців у другій коробці?

2. клас 53

2. В одній коробці 6 олівців, а в другій -на 4 олівці більше. Ски олівців у двох коробках разом?

Деякі учні другу задачу розв’язують однією дією, як і їм потрібно пояснити: для того щоб дізнатися, скільки олі зом у двох коробках, треба знати, скільки олівців у першій

1. скільки у другій. Скільки у першій відомо, а скільки у ) необхідно спочатку знайти. Дія 6 + 4 = 10 -це іє обчислен кості олівців у другій коробці, бо на 4 більше означає “сті. та ще 4”. Отже, задача мусить мати ще й другу дію: 6 + 1( всього олівців у двох коробках.

Наведена робота вчить учнів уважно вивчати умову і з, ня задачі, щоб зрозуміти, проста вона чи складена, усві структуру задачі.

Методика роботи над складеними задачами в 2 кл

Як уже було сказано, розбір задачі можна проводити способами: від числових даних і від запитання. Вважаєть розбір від запитання доцільно проводити, коли задача лег: нашу думку, розбір від запитання, як більш цінний для рог го розвитку дітей, учитель повинен здійснювати в усіх виг коли для цього є найменша можливість. Багато учителів вляються від нього через брак часу на уроці. Звичайно, *

2. класі цим способом знехтувати, то у наступних класах і роботи над важчими задачами обов’язково бракне часу. Але

3. самого початку, на задачах на дві дії відпрацювати розі запитання, це в майбутньому дасть резерв часу, бо багато зможуть розв’язувати задачі самостійно, без допомоги вч Адже у них виробиться самостійне мислення, аналітичне м. ня, логічне мислення!

Конкретні приклади розбору задач у 1

Для приготування юшки мама взяла з кошика 8 підберезників 10 маслюків. Після цього в кошику залишилося 12 грибів. Скілі ки грибів було у кошику спочатку?

І етап. Про що говориться у задачі? (Про гриби, які брала з кошика.) Скільки підберезників узяла мама? (8.) Ск маслюків? (10.) Скільки грибів після цього залишилося в і

Р (12.) Про що запитується в задачі? (Скільки грибів було у вику спочатку? )

Водночас з аналізом змісту задачі вчитель може робити на до- і короткий запис. (Коли діти стежать за процесом його утво- ася, вони краще розуміють структуру запису.)

Було - ?

Спідберезників - 8 Взяла <

[маслюків -10

Залишилося -12 гр.

2. Етап. Наведемо обидва способи розбору: від числових даних від запитання.

• Розбір від числових даних.

• Якщо у задачі відомо, що мама взяла 8 підберезників і 10 мас­ив, то про що можна дізнатися? (Скільки всього грибів взяла иа з кошика.) А коли буде відомо, скільки грибів мама взя- і скільки грибів у кошику залишилося, то про що можна буде натися? (Скільки грибів у кошику було спочатку.) Отже, про що наємося спочатку? (Скільки грибів мама взяла з кошика.) Якою ю? (Дією додавання.) Про що дізнаємося після цього? (Скільки ібів було в кошику спочатку.) Якою дією? (Дією додавання.) ї до чого будемо додавати? (Кількість грибів, які залишилися, кількості грибів, які мама взяла.) Чому будемо додавати? (Бо татку в кошику грибів було більше, ніж залишилося потім.)

2. етап. Доцільно, щоб у більшості задач учні виконували го самостійно.

1. 8 + 10 = 18 (гр.)

2. 12 + 18 = ЗО (гр.)

Відповідь: ЗО грибів.

2. етап. Перевірка правильності відповіді.

• Якщо спочатку було 30 грибів, а мама забрала 8 і 10 грибів, скільки грибів має залишитися? (12.) Учні усно обчислюють:

• 8 = 22 (гр.); 22 - 10 = 12 (гр.). Отже, задача розв’язана пра­льно.

Під час складання плану розв’язування задачі вчитель сам рішує, чи потрібно уточнювати вибір тієї чи іншої дії. У цій задачі ми вибір першої дії не уточнювали, оскільки пер має в основі просту задачу на знаходження суми, яка не вить труднощів для учнів; вибір другої дії варто уточнити, основі лежить задача на знаходження невідомого зменшуі Простих задач цього виду учні розв’язали значно менше, і дач на знаходження суми.

• Розбір від запитання.

Повний аналіз.

Учитель може супроводжувати бесіду зображенням на схеми повного аналізу.

• Чи можемо ми відразу дізнатися, скільки грибів булс шику спочатку? (Ні, не можемо.)

• Які дві величини для цього потрібно знати? (Скільки мама взяла з кошика і скільки грибів у ньому залишилося

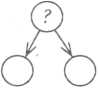
- Яка з цих двох величин нам відома, а яка невідома? (В що залишилося 12 грибів. Невідомо, скільки грибів мама ві кошика.)

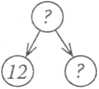
- Чи можемо ми дізнатися, скільки грибів мама взяла шика? (Можемо.) Які дві величини для цього маємо? (У з сказано, що мама взяла 8 підберезників і 10 маслюків.)

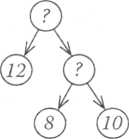
- Про що дізнаємося спочатку? (Скільки грибів мама взяла тшика.) Якою дією? (Дією додавання.) Що будемо додавати? ііькосші маслюків і підберезників.)

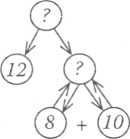
• Про що дізнаємося потім? (Скільки всього грибів було в ко­шаі спочатку.) Якою дією? (Дією додавання. До 12 грибів, що шшилися, додамо ті гриби, які мама взяла з кошика.)

• Отже, до 12 додамо те число, яке вийде у першій дії:

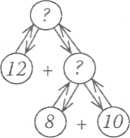
За такою схемою неважко записати розв’язання самостійно.

Якщо є потреба уточнити вибір другої дії, то це можна зробити ■ьх:

• Після першої дії ми вже знатимемо, скільки грибів мама с-рала і скільки залишилося:

Було - ?

Забрала - [І]

| Залишилося - Ц

• З яких двох частин складаються гриби, які були у кошику ючатку? (З тих, що мама забрала, і тих, що залишилися.) То і знайти ціле, коли відомі частини? (Треба частини додати.) рже, якою дією ми закінчимо розв’язування? (Дією додавання.)

Проведена бесіда важлива не лише для розв’язування цієї за- ічі. Учні отримують і загальнорозумові вміння: слухати запи- іння вчителя і давати на нього точну відповідь; користуватися >ротким записом під час пошуку відповіді на запитання вчителя;

розуміти схему повного аналізу і користуватися нею як під] під час самостійного запису розв’язання задачі та ін.

Для того щоб учні швидше набули цих умінь, учитель го боку повинен сприяти цьому під час бесіди. Деякі вчит чатківці після того, як короткий запис зроблено, забуваю нього. У дітей створюється враження, що він не потрібні свідчений учитель постійно використовує короткий запис, використання короткого запису - це свого роду мистєцте велику роль відіграють не лише слова вчителя, а й міміка і Коли діти затруднюються відповісти на чергове запитання, указкою певного числа чи слова у запису наштовхує їх в вильну відповідь. Нерідко вчитель не поспішає показуваті побачити, на скільки учні розуміють його, і лише отримав е повідь, показує у запису те місце, яке її підтверджує чи сг вує і т. д.

Інколи вчитель ставить запитання, а окремі учні, випере чи аналіз, дають вже готову відповідь або відповідають на наї запитання, яке ще не прозвучало. Вчитель може навіть пері аналіз, бо, мовляв, дітям і так усе зрозуміло. Звичайно, в ок випадках можна вчинити і так. Проте помилкою є системі йти на повідку в учнів. Адже бесідою повинен керувати не у* вчитель. У класі є багато учнів, які потребують розбору. Таї втрачають шанс самим брати участь у процесі міркування г: дачею. Вони приречені пасивно сприймати готові відповіді ти мислить швидше. Саме це і є причиною того, що так багате у класі не можуть самостійно розв’язувати задачі. А те, що ; класі ще можна виправити, у 4-му вже стає невиправним.

А як бути із потребами сильних учнів? Адже вони по ють більш швидкого темпу роботи. Коли вчитель бачить, що учні готові відразу розв’язувати задачу, він проводить диц ційовану роботу: сильні учні розв’язують задачу самостійн нак їм заборонено брати участь у бесіді, яку організовують штою учнів. Тоді слабші звикають, що їм самим треба мірк над запитаннями вчителя і давати на них відповідь.

Учитель пишається сильними учнями і це його право. Г на нашу думку, предметом найбільшої гордості має бути в учень, який обдарований від природи, а той, хто має менші ності, але навчився мислити виключно завдяки вмілій метод роботі вчителя.

Проте сильним учням теж час від часу корисно брати участь у аагальній бесіді: вона вчить витримки і дисциплінованості, фор­мує вміння давати точну відповідь на запитання вчителя, вироб- жяє культуру мислення і спілкування, без якої важко обійтися в майбутньому. Адже не завжди задачі будуть так легко даватися. Коли учень зустрінеться з дійсно складною задачею, він зможе її яодолати, якщо засвоїв уроки поступового пошуку.

Попередню задачу ми розібрали від запитання за допомогою зобного аналізу. Це означає, що кожного разу вчитель з’ясовує, які дзі величини потрібні, щоб знайти шукану. Зазвичай, одна з цих дзох величин у задачі відома. Тому при розборі задачі можна обме­житися і неповним аналізом, при якому називають щоразу лише невідому величину. Неповний аналіз роблять тоді, коли вчитель упевнений, що діти відразу зрозуміють, яка саме величина стано­вить проблему. Зручно користуватися неповним аналізом під час ■розбору задач, що включають різницеве або кратне відношення.

Розглянемо приклади.

Першого дня бригада відремонтувала 28 м дороги, другого - на 13 м більше, ніж першого, а третього - на 7м менше, ніж другого. Скільки метрів дороги відремонтувала бригада третього дня?

І - 28 м «£-

II - на 13 м більше -><■

III - ?, на 7 м менше -

Неповний аналіз (від запитання).

- Чи можемо ми відразу дізнатися, скільки метрів дороги відремонтувала бригада третього дня? (Ні, не можемо.) Чому? (Бо ми не знаємо, скільки метрів бригада відремонтувала другого 9ня.) А чи можемо дізнатися, скільки другого? (Так.) Чому? (Бо <сказано, що першого дня бригада відремонтувала 28 м, а другого - -а 13 м більше.) То про що дізнаємося у першій дії? Якою дією? У другій? І т. д.

Розглянемо ще кілька випадків різних видів розбору.

В одному лотку 10 яєць, у другому - ЗО, а в третьому - у 2 рази менше, ніж у перших двох лотках разом. Скільки яєць у тре­тьому лотку?

II-2С

І- 10

III - ?, у 2 рази менше -

Неповний аналіз.

Чи можемо ми відразу дізнатися, скільки яєць у третьому ку? (Ні, бо ми не знаємо, скільки яєць у першому і другому ках разом.) А чи можна дізнатися, скільки яєць у перших лотках разом? (Так, бо сказано, що в першому лотку 10 яв в другому - ЗО.) То про що дізнаємося спочатку? (Скільки в яєць у перших двох лотках разом.) Якою дією? (Дією додава\ Про що дізнаємося після цього? (Скільки яєць у третьому ку.) Якою дією? (Дією ділення.) Чому ділення? (Бо сказане в третьому лотку у 2 рази менше яєць, а щоб зменшити чш 2 рази, треба його поділити на 2.)

Зауважимо, що коли розбір дійшов до моменту, коли відповіли “Можемо”, варто спочатку запитати “Чому може» а вже тоді “Як?” Якщо діти свідомо відповіли “Можемо”, : як доказ наведуть ту частину умови задачі, яка це підтверд; Якщо ж дитина не може цього зробити, отже, вона, швидіг все, вгадує дію.

У домашній бібліотечці було 40 книжок. Ігор вже прочитав 15 книжок. На скільки більше книжок Ігорю залишилося про­читати, ніж він уже прочитав?

На ? більше

Було - 40 кн. Прочитав - 15 кн. Залишилося - ?

• Розбір від числових даних.

- Якщо в задачі сказано, що всього книжок 40, а Ігор прочитав 15, то про що можна дізнатися? (Скільки книжок Іг залишилося прочитати.)

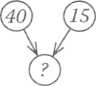
- А коли буде відомо, скільки книжок Ігор уже прочитав і їаьки йому залишилося прочитати, про що зможемо дізнатися? Ія скільки книжок більше Ігорю залишилося прочитати, ніж к уже прочитав.)

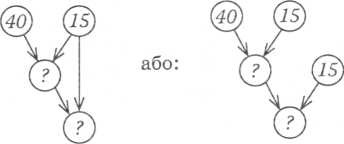
— То про що дізнаємося у першій дії? (Скільки книжок Ігорю їлишилося прочитати.) Якою дією? (Дією віднімання.) Про що знаємося другою дією? (На скільки більше книжок залишило- и ніж прочитав.) Яку дію виконаємо? (Дію віднімання.) Чому? Щоб дізнатися, на скільки одне число більше від другого, треба в більшого числа відняти менше.) Що від чого будемо віднімати другій дії? (Від результату першої дії віднімемо 15.)

В Оксани було 12 фломастерів і 20 олівців. 4 олівці вона пода­рувала подрузі. На скільки менше стало в Оксани фломастерів, ніж олівців?

На ?менше

)

• Розбір від запитання.

Повний аналіз.

61

- Чи можна відразу дізнатися, на скільки менше стало в Ок- антт фломастерів, ніж олівців? (Ні.) Які дві величини потрібно ;ля цього знати? (Скільки було фломастерів і скільки залишило- х олівців.) Що нам з цього відомо, а що невідомо? (Відомо, що іломастерів було 12, а невідомо, скільки залишилося олівців.) і. чи можемо ми дізнатися, скільки олівців залишилося? (Так, бо адомо, що Оксана мала 20 олівців і з них 4 подарувала подрузі.) Го про що дізнаємося спочатку? (Скільки олівців залишилося в Уксани.) Якою дією? (Дією віднімання.) Про що дізнаємося піс-

? клас

ля цього? (На скільки стало менше фломастерів, ніж олі Якою дією? (Дією віднімання.) Чому саме дією віднімання? дізнатися на скільки одне число менше від другого, потрібі більшого числа відняти менше.)

У цьому випадку варто поцікавитися, чому друга дія - : мання, бо деякі учні можуть дати неправильне обґрунтуй “Бо в задачі сказано: менше.” Це означатиме, що дитина п, задачу на різницеве порівняння із задачею на зменшення чис кілька одиниць. Якщо не виправити цей недолік, то в майбу му в задачах із запитанням “На скільки більше...?” дитина самої причини вибере дію додавання.

Галинка попрасувала 5 носових хусточок, а її сестра - 13. Ус хусточки дівчатка розклали порівну в шафі на 3 полиці. Скіль­ки хусточок поклали на кожну полицю?

Галинка - 5 х. 'і

} Розклали на 3 полиці по ? х.

Сестра - 13 х. І

• Розбір від числових даних.

- Якщо відомо, що Галинка попрасувала 5 хусточок, а їі тра - 13, то про що можна дізнатися? (Скільки всього хуст попрасували дівчатка.) А коли буде відомо, скільки всього точок розклали порівну на 3 полиці, про що дізнаємося? (Скі хусточок на одній полиці.) То про що дізнаємось у першій (Скільки всього хусточок попрасували дівчатка.) Якою д (Дією додавання.) Про що дізнаємось у другій дії? (Скільки точок клали на кожну полицю.) Якою дією? (Дією ділення.) ^х ділення? (Бо сказано: розклали порівну на 3 полиці. Це ознс число поділити на три рівні частини.)

Короткий запис не завжди потрібно виконувати на дошці, рисно, щоб діти самостійно пробували його виконати. Адже і підказкою до розв’язування задачі. Якщо учень сам його викс це допоможе йому правильно розв’язати задачу під час самості роботи на уроці чи вдома. І хоча вміння коротко записувати за; програмою не вимагається, варто сприяти учням у його надбан

Коли умова задачі “заплутана”, короткий запис дуже поі ний у фронтальній роботі (див. попередню задачу про фломаст і олівці). А загалом учитель сам вирішує, чи використовувати даної конкретної задачі короткий запис і в якій формі.

Розв’язування задач виразом

2-му класі розпочинається важлива робота: навчання учнів =£з язувати задачу виразом.

' Підготовчий ступінь розпочинається перед вивченням нумера- I чисел 21-100, коли учні знайомляться з виразами на дві дії Иужками. На цьому ступені діти повинні засвоїти, що сума чи шгпя - це не лише результат дії, а й вираз. Наприклад, 6 + 2 - і- гума чисел 6і2;9-3-це різниця чисел 9 і 3. Якщо суму чи ■еншо потрібно додати чи відняти від іншого, числа, її беруть у втун- 6 - (3 + 1); 8 + (9 - 2) і т. д. Якщо вираз містить дужки, ► хя в дужках виконується першою. Діти вчаться записувати уаи з дужками під диктування вчителя. Спочатку вони мають 533%' із задачами абстрактного характеру:

-до числа 6 додати суму чисел 5 і 2;

: - від числа 20 відняти різницю чисел 14 і 4.

Пізніше вводяться сюжетні задачі, за умовою яких складено фьзи. Учні повинні пояснити, про що можна дізнатися, обчис- т—'■* ці вирази. Спочатку це вирази на одну дію, потім - на дві.

За день магазин продав 8 комп’ютерів і 5 телевізорів. Про що шснл дізнатися, обчисливши вирази: 8 + 5; 8 - 5?

Можна запитати в учнів, як називається перший вираз; дру- к вираз. (Сума; різниця.) Що може означати сума для задачі в комп’ютери і телевізори? (Скільки разом комп’ютерів і теле- хрів продав магазин.) Що означає різниця 8 - 5? (На скільки шиїе комп’ютерів, ніж телевізорів, продав магазин.)

- У трьох вазах 80 квіток. У першій вазі ЗО квіток, а у другій - 27. Про що можна дізнатися, обчисливши такі вирази: ЗО - 27;

_: ЗО + 27; 80 - ЗО; 80 - 27; 80 - (ЗО + 27)?

Із виразами на одну дію діти не повинні відчувати труднощів, Юте необхідно звернути їхню увагу на різницю у трактуванні ви­віз ЗО - 27 і 80 - 27. Перший вираз означає, на скільки більше ігок у першій вазі, ніж у другій; другий вираз - скільки всього вток у першій і третій вазах разом. Одна й та сама дія може мати вне трактування; дія віднімання може трактуватися як сума.

У роботі із виразом на дві дії треба запитати в учнів, яка дія жонується першою. (Дія в дужках.) Як називається вираз у жках? (Сума.) Що ця сума означає у нашій задачі? (Скільки ього квіток у першій і другій вазі разом.) Яка у виразі наступна я? (Дією віднімання.) Що від чого віднімається? (Від усієї кіль­

кості квіток віднімається кількість квіток у першій і дру. разом.) Про що ми дізнаємося? (Про кількість квіток у ? вазі.)

У кінці вивчення нумерації 21-100 подається зразок зання задачі складанням виразу. Вираз складається пост> усним поясненням.

У кондитерському відділі було 9 тортів. До обіду відділ прод,

6 тортів. Після цього у відділ завезли ще 7 тортів. Скіль, тортів стало у відділі?

Можна спочатку розв’язати задачу окремими діями, а ^г готовим розв’язанням учити дітей складати вираз.

1. 9-6 = 3 (т.)

2. 3 + 7= 10 (т.)

- Сьогодні ми навчимося записувати розв’язання задачі данням виразу. Подивіться на першу дію і скажіть, що ог вираз 9-6. (Стільки тортів залишилося у відділі після . жу 6 тортів.) У другій дії ми до значення цього виразу,

З, додаємо 7. Але ж ми знаємо, що 3 = 9-6. Спробуємо у і дії замість числа 3 підставити вираз 9-6. Який вираз ми маємо? ((9-6)3- 7.) Обчисліть його значення усно. (9 — і З + 7=10. Отже, (9-6)3- 7 = 10.) Ви помітили, що віді така сама. Отже, замість того щоб записувати розв’язання : двома діями, ми можемо записати його одним виразом на д (9-6) + 7 = 10 (т.). Давайте ще раз пригадаємо, як ми утв( цей вираз. (Результат першої дії ми не обчислювали і піде, ли у другу дію замість першого доданка вираз 9 - 6.)

Кілька наступних задач можна опрацювати таким самта собом: спочатку розв’язати задачу діями, а тоді — виразом. У бутньому діти отримують завдання відразу записувати вира розв’язування діями, причому на перших порах вираз склад поступово з поясненням:

9 - 6 - залишилося тортів до обіду;

(9 - 6) + 7 - стало всього тортів;

(9-6)+7= 10 (т.)

У подальшій роботі вчитель щоразу сам повідомляє учня: оформити запис розв’язання задачі: окремими діями чи склі ням виразу.

З КЛАС

Основні види складених задач, які розглядаються в 3 класі

У 3 класі продовжується робота над задачами на дві дії і зжяються задачі на три дії. Багато видів задач на дві дії уже

вглядалися у 2 класі, але є й нові. Серед них задачі на знаход- кня числа, яке задане подвійним відношенням (різницевим і

етннм; двома кратними), велика група задач на кратне порів- юя двох чисел, одне з яких відоме, а друге є результатом пер- к дії, та ін. У 3 класі починається вивчення так званих типо- е задач; значна частина задач на дві дії є типовими задачами зваходження четвертого пропорційного (про типові задачі буде ваво окремо).

Задачі на три дії можна поділити на три групи: а) задачі, ут- я&гі шляхом “розширення” задач на дві дії (у тому числі і типо- к задач); б) задачі на знаходження суми (різниці, частки) двох їутхів (сум, різниць, часток); в) задачі, обернені до задач на входження суми двох добутків.

Перейдемо до розгляду конкретної методики роботи над цими

Методика роботи над складеними задачами в 3 класі