4. Самостоятельное вычисление корреляции

Поскольку экономическая ситуация в странах не является постоянной, то идеальным способом отследить направление развития рождаемости населения является самостоятельное вычисление корреляции. Вам наверняка покажется это чрезвычайно сложным занятием, но процесс вычисления можно упростить, воспользовавшись Microsoft Excel: достаточно лишь ввести численные данные различных стран по уровню доходов и уровню рождаемости за какой-либо период и воспользоваться специальной функцией.

Опишем процесс подсчета корреляции. Для начала соберем численные данные интересующих нас показателей и сгруппируем их в таблицу, состоящую из двух столбцов. Первый из которых содержит данные о затратах стран на семейную политику, а второй - об уровне рождаемости. Каждая строка таблицы будет соответствовать определенной стране. В конце столбцов в пустой ячейке впишем «=КОРРЕЛ». Затем выделите данные в одном столбце, поставьте запятую и выделите второй столбец. Полученная цифра соответствует искомому значению корреляции.

5. Пример вычисления корреляции

Для характерного примера возьмем средние данные следующих стран: США, Франция, Норвегия, Дания, Финляндия, Великобритания, Швеция и Чехия.

	Рождаемость, %	Затраты на семейную политику, %
США	0,51	2,01
Франция	2,95	1,95
Новергия	3,43	1,77
Дания	3,6	1,77
Финляндия	3,54	1,77
Великобритания	2,29	1,61
Швеция	3,75	1,55
Чехия	2,2	1,15
		-0,139603151

1. Чтобы определить корреляцию, применим формулу:

– ковариация случайных величин .

– среднеквадратичное отклонение .

2. Для того, чтобы отыскать ковариации и среднеквадратичные отклонения случайных величин, необходимо сначала найти их математические ожидания:

В нашем случае математическое ожидание величин можно найти с помощью среднего арифметического, значит:

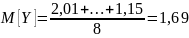
3. Найдем дисперсию по формуле:

Чтобы облегчить вычисления, сведем все в таблицу:

х-х	y-y	(x-x)^2	(y-y)^2
-2,27375	0,3125	5,169939063	0,09765625
0,16625	0,2525	0,027639063	0,06375625
0,64625	0,0725	0,417639063	0,00525625
0,81625	0,0725	0,666264063	0,00525625
0,75625	0,0725	0,571914063	0,00525625
-0,49375	-0,0875	0,243789063	0,00765625
0,96625	-0,1475	0,933639063	0,02175625
-0,58375	-0,5475	0,340764063	0,29975625

4. Далее определим среднеквадратичное отклонение наших величин по формуле:

5. Определим ковариацию по формуле:

Для упрощения сведем в таблицу данные:

х-х	y-y	(х-х)(y-y)
-2,27375	0,3125	-0,71055
0,16625	0,2525	0,041978
0,64625	0,0725	0,046853
0,81625	0,0725	0,059178
0,75625	0,0725	0,054828
-0,49375	-0,0875	0,043203
0,96625	-0,1475	-0,14252
-0,58375	-0,5475	0,319603

Тогда искомая ковариация:

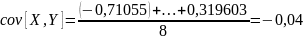
6. Применим формулу из 1) пункта:

Искомая корреляция равна -0,14. Если коэффициент корреляции отрицательный, это означает наличие противоположной связи: чем выше значение одной переменной, тем ниже значение другой.