9.4. Технологія регресійного аналізу у gpss World
Убудовані у GPSS World автоматичні генератори експериментів дозволяють проводити регресійний аналіз за ПФЕ або ДФЕ з метою побудови рівняння поверхні відгуку за заданими факторами і визначати чисельне значення оптимуму. У GPSS World регресійний аналіз носить назву оптимізуючого експерименту.
Користувач задає вихідні умови, а GPSS World автоматично створює план і проводить з поверхнею відгуку експеримент, який відшукує оптимальне значення. Максимально можлива кількість змінних вхідних факторів в оптимізаційному експерименті GPSS World дорівнює п’яти. Фактори визначаються за допомогою оператора EQU або змінних. В ході експерименту GPSS World намагається підібрати або лінійну модель, або модель у вигляді поліному другого порядку, включаючи двофакторну взаємодію.
Розглянемо на прикладах проведення регресійного аналізу (оптимізуючого експерименту) у GPSS World. У прикладі 9.2 розглядається вплив одного фактора на відгук моделі, а у прикладі 9.3 досліджується вплив двох факторів.
Приклад 9.2. Транспортна фірма в своєму розпорядженні має деяку кількість вантажних автомобілів і кран. Кран, відправляється на об’єкт, де він розвантажуватиме автомобілі з інтенсивністю 15±2 хвилини. Автомобілі під‘їзджатимуть з будматеріалами, ставатимуть у чергу і, після звільнення крану, розвантажуватимуться та знову відправлятимуться за новими будматеріалами. В середньому, на такий маршрут затрачатиметься 60±8 хвилин. Дохід від одного розвантаженого автомобіля становить 500 одиниць вартості. Використання крана обходиться в 2000 одиниць вартості в день, а на обслуговування автомобілів затрачається 1000 одиниць вартості в день. Потрібно визначити, яку кількість автомобілів слід придбати транспортній фірмі, щоб дохід від підприємництва був максимальним. Моделювання необхідно виконати для одного робочого дня (8 годин).
Модель розробленої системи наведена на рисунку 9.12.
Для проведення регресійного аналізу виконуємо наступні команди: Edit ► Insert Experiment ► Optimazing… (Правка ► Вставити експеримент ► Оптимізуючий...). Відкриється діалогове вікно Optimizing Experiment Generator (Генератор оптимізуючого екперименту) (рис 9.13).
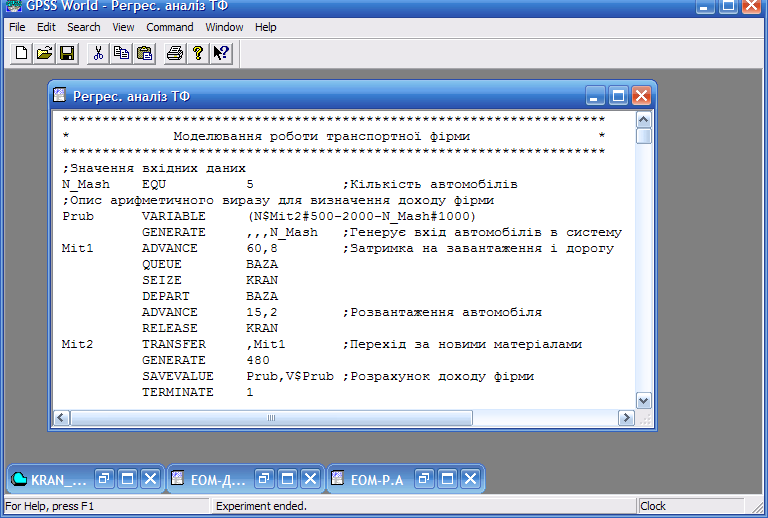
Рис. 9.12. Модель роботи транспортної фірми
В поля Experiment Name (Назва експерименту) і Run Procedure Name (Назва процедури запуску) задаємо назву експерименту Regres_Analiz і назву Run-процедури прогонів моделі Regres_Analiz_Run.
Далі розміщена група полів Initial Local Experimental Region (Задання локальної експериментальної області). Потрібно вказати фактори (не більше п’яти – A, B, C, D, E) і для кожного з них два рівня Value1 і Value2. У нашому прикладі досліджується вплив одного фактора N_Mash на відгук моделі – дохід фірми.
Назва цього фактора і значення його рівнів, вводяться у відповідні поля вікна Optimizing Experiment Generator (рис. 9.13). У поле Expression (Вираз) групи Result (Результат) вводиться назва комірки X$Prub, в якій зберігається результат. Перемикачі Maximize – Minimize встановлюють напрям оптимізації. Згідно умови прикладу нас цікавить максимальне значення доходу, тому залишаємо Maximize.
Поля Low Limit і High Limit в Movement Limits (Межі пересування) дозволяють обмежити переміщення локальної експериментальної області в оптимізуючому експерименті. В них можна задати максимальні межі для кожного фактору. У більшості випадків можна використовувати значення за замовчуванням – 0 і 100. Задання величини Redirection Limit (Межа зміни напрямку) обмежує кількість змін напрямку руху експерименту у факторному просторі. В ці поля вводяться відповідні дані (рис. 9.13).
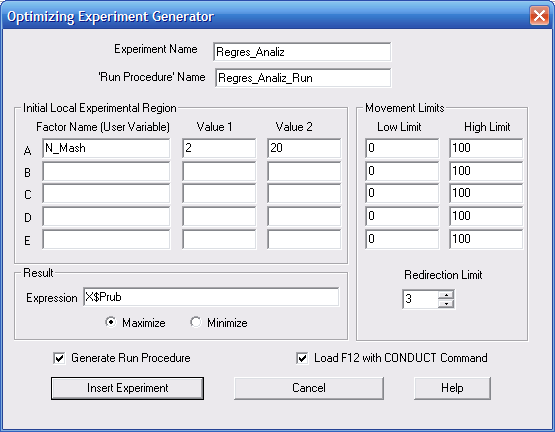
Рис. 9.13. Діалогове вікно Optimizing Experiment Generator
Встановлені прапорці для вибору опцій Generate Run Procedure і Load F12 with CONDUCT Command створюють процедуру прогонів моделі і дозволяють після створення об’єкта моделювання запускати експеримент функціональною клавішею F12.
Уся необхідна інформація введена у відповідні поля. Натискаємо кнопку Insert Experiment (Вставити експеримент) для запуску автоматичного генерування експерименту. З’явиться діалогове вікно, що дозволяє відредагувати процедуру запуску так само, як і у дисперсійному експерименті. Після коригування натискаємо кнопку Оk. Автоматично згенеровані Plus-оператори з’являться в нижній частині моделі.
Для запуску експерименту спочатку створюємо об’єкт моделювання, натиснувши комбінацію клавіш Ctrl+Alt+S, а потім натискаємо функціональну клавішу F12.
Експеримент почне виконуватись. У вікно Journal (Журнал) процесу моделювання будуть виводитись звіти про стан і результати кожного спостереження. За ними можна дізнатись про переміщення в локальній експериментальній області до оптимальних умов. Якщо це відбувається, або якщо досягнута межа зміни напрямку або межа переміщення, проведення експерименту завершується.
У вікні Journal (Журнал) також виводяться результати перевірки критерію адекватності і рівняння знайденої поверхні відгуку. Plus-експеримент намагається перевірити прогнозовані оптимальні умови, запустивши процес моделювання для них.
Результати регресійного аналізу (оптимізуючого експерименту), отримані після виконання двадцяти спостережень, наведені на рис 9.14.
Отримане рівняння поверхні відгуку має вигляд:
Y = 1084.36 + 823.045 A – 57.6132 A^2.
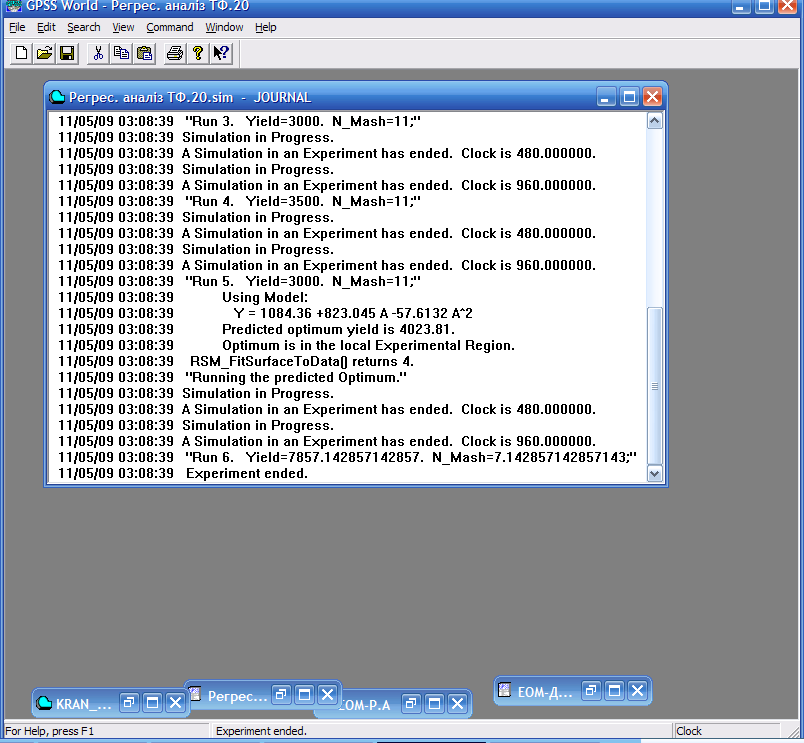
Рис. 9.14. Результати регресійного аналізу
Знайдене оптимальне значення вхідної змінної N_Mash = 7.142857142857143, та вихідної змінної Yield = 7857.142857142857. Отже, з урахуванням умови цілочисельності транспортній фірмі для отримання максимального доходу слід придбати сім автомобілів.
Приклад 9.3. Транспортна фірма в своєму розпорядженні має деяку кількість вантажних автомобілів марки МаЗ і КамаЗ, а також кран. Кран, відправляється на кар’єр, де він завантажуватиме з інтенсивністю 102 і 202 хвилин автомобілі марки МаЗ і КамаЗ відповідно. Після завантаження автомобілі відправляються на об’кт де розвантажуються та знову повертаються на кар’єр за новими матеріалами. В середньому, на такий маршрут затрачатиметься 30±5 хвилин. Дохід від одного розвантаженого автомобіля марки МаЗ становить 480 одиниць вартості, а від автомобіля марки КамаЗ – 560 одиниць вартості. На обслуговування крана, автомобіля марки МаЗ і автомобіля марки КамаЗ затрачається 200, 90 і 95 одиниць вартості в день відповідно. Потрібно визначити, яку кількість автомобілів якої марки слід придбати транспортній фірмі, щоб дохід від підприємництва був максимальним. Моделювання необхідно виконати для десяти робочих (8 годинних) днів.
Модель розробленої системи наведена на рисунку 9.15.
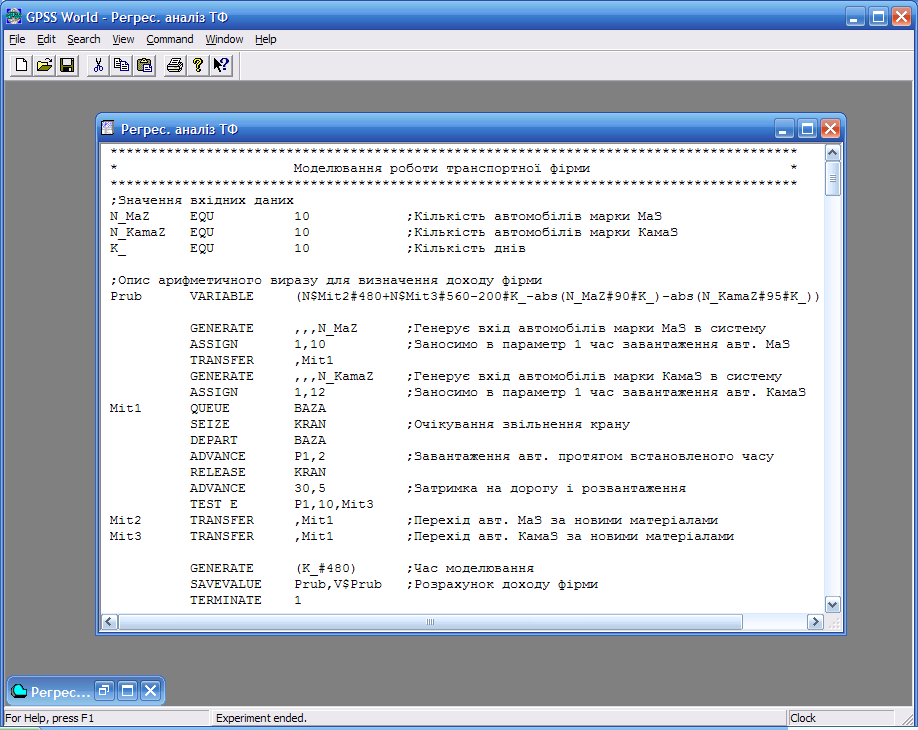
Рис. 9.15. Модель роботи транспортної фірми
У цьому прикладі досліджується вплив двох факторів N_MaZ і N_KamaZ на дохід фірми (відгук системи).
Імена цих факторів і значення їхніх рівнів вводяться у вікно Optimizing Experiment Generator, як показано на рис. 9.16.
Для проведення регресійного аналізу виконуються такі ж кроки, як і для попереднього прикладу.
Результати регресійного аналізу (оптимізуючого експерименту), отримані після виконання двадцяти спостережень, наведені на рис 9.17.
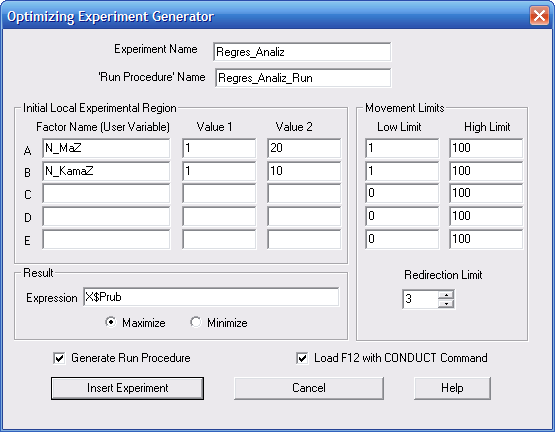
Рис. 9.16. Діалогове вікно Optimizing Experiment Generator
Отримане рівняння поверхні відгуку має вигляд
Y=95776.6+11102 А+17872.8 В–638.129 А В–170.334 A^2–709.76 В^2.
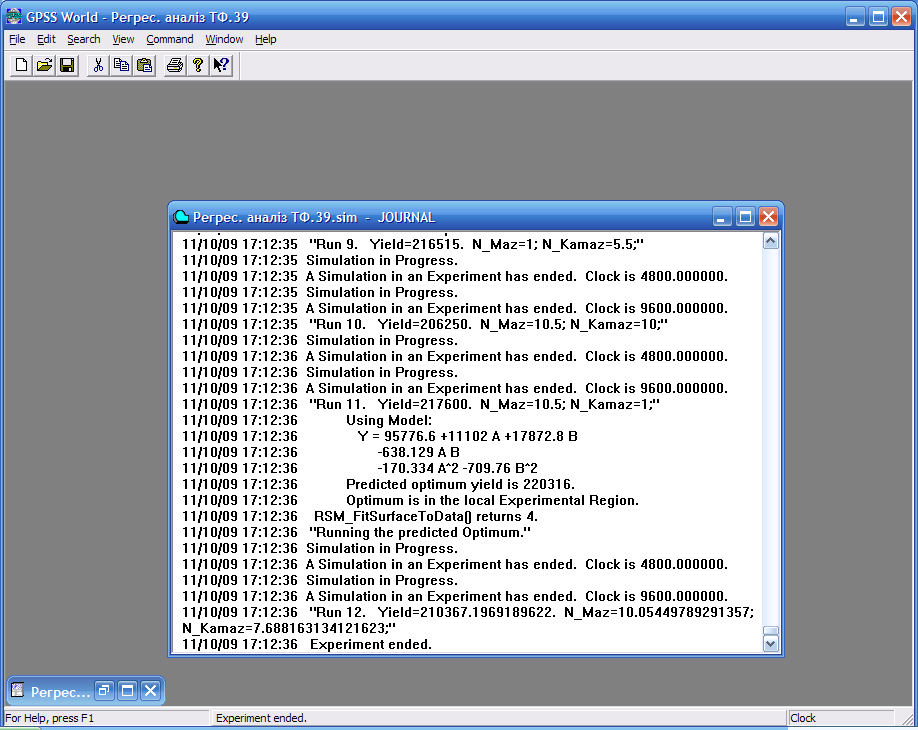
Рис. 9.17. Результати регресійного аналізу
Знайдені оптимальні значення вхідних змінних N_MaZ = 10.05449789291357 і N_KamaZ = 7.688163134121623, та вихідної змінної Yield = 210367.1969189622. Отже, транспортній фірмі для отримання максимального доходу слід придбати десять автомобілів марки МаЗ і вісім автомобілів марки КамаЗ.
Розглянемо ще один приклад застосування регресійного аналізу
Приклад 9.4. Провести оптимізуючий експеримент для пошуку экстремума функції двох змінних z = 100 – (x – 20)2/9 – (у – 30)2/16, що являє собою верхню частину еліптичної поверхні.
Модель регресійного аналізу для прикладу 9.4 наведена на рис. 9.18.
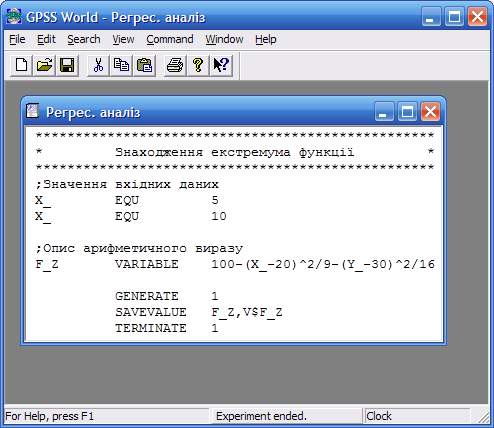
Рис. 9.18. Модель для знаходження экстремума функції
Вибераємо Edit ► Insert Experiment ► Optimazing… (Правка ► Вставити експеримент ► Оптимізуючий...). У діалоговому вікні Optimizing Experiment Generator (Генератор оптимізуючого екперименту) вводяться відповідні дані, як показано на (рис 9.19).
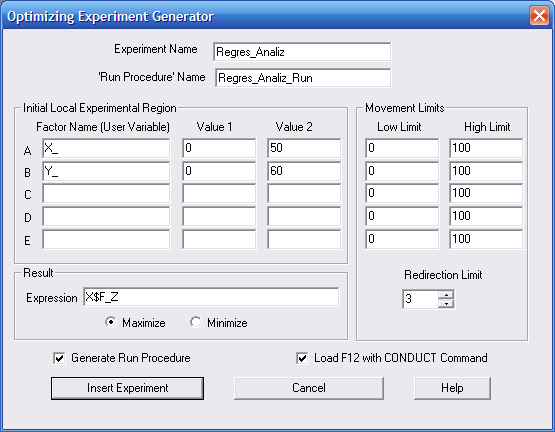
Рис. 9.19. Діалогове вікно Optimizing Experiment Generator
В поля Experiment Name і Run Procedure Name вводяться Regres_Analiz і Regres_Analiz_Run відповідно. В групу полів Initial Local Experimental Region вказуються імена факторів і значення їхніх рівнів.
У поле Expression групи Result задається назва комірки X$F_Z для зберігання результату спостереження. Залишається перемикач на Maximize. Також встановлюються прапорці для вибору опцій Generate Run Procedure і Load F12 with CONDUCT Command.
Після натискання кнопки Insert Experiment відкриється вікно Run Procedure Generation, у якому відображається автоматично згенерований текст Run-процедури. Після її коригування натискаємо Ок. Автоматично згенеровані Plus-оператори з’являться в нижній частині моделі. Виконавши пункт меню Command ► Create Simulation, відкомпілюємо модель. Зауважимо, що всі процедури реєструються. Натиснемо клавішу F12 і почнемо експеримент. У вікні Journal буде представлена наступна інформація про хід експерименту (рис. 9.20).
Отримане рівняння поверхні відгуку має вигляд:
Y=55.5556 – 1.11111 A + 4.62963 B – 0.1111111 A^2 – 0.0625 B^2.
Знайдені оптимальні значення (вхідні змінні x_ = 20, у_ = 30, вихідна змінна Yield = 100) збігаються з теоретичними.
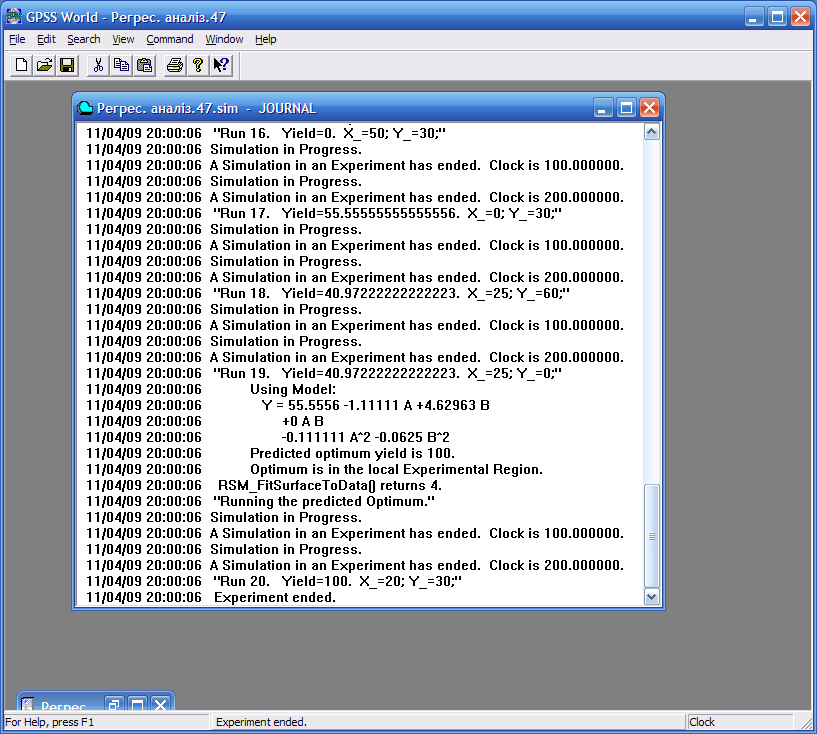
Рис. 9.20. Результати регресійного аналізу