2. Вхідний потік вимог

Вхідний потік є певною послідовністю вимог, які надходять до обслуговуючої системи у деякі моменти часу. Для описання вхідного потоку вимог необхідно задати інтервал часу t_k = t_k – t_k-1 між сусідніми моментами часу t_k-1 і t_k (закон надходження) та кількість вимог k (k = 1, 2, ...), які можуть надійти одночасно.

Основною характеристикою потоку вимог є інтенсивність . Це серед­нє число вимог, що надходить за одиницю часу. Величина  = 1/визначає середній інтервал часу між двома послідовними вимогами.

Потік називається детермінованим, якщо вимоги надходять у систему через строго фіксовані проміжки часу, а інтервали часу t_1k між сусідніми ви­­­могами приймають наперед відомі значення. Якщо ще й інтервали одина­ко­ві (t₁ = t₂ =.. = t_k =... t), то потік називається регулярним (рис. 1.7, а).

Випадковим називається такий потік, для якого вимоги надходять в обслуговуючу систему одна за одною у довільні моменти часу (t₁ ≠ t₂ ≠ ... ... ≠ t_k), а інтервали часу t_k є випадковими величинами (рис. 1.7, б).

Характеристикою випадкового потоку є задавання розподілу випадкових величин F_k (t_n) усіх інтервалів t_k (k = 1, 2, …).

Найпростішим називається такий потік, який одночасно має власти­вос­ті стаціонарності, ординарності та відсутності післядії.

Випадковий потік вважається стаціонарним, якщо ймовірність попа­дання того чи іншого числа вимог на проміжок часу довжиною t залежить лише від довжини цього проміжку та не залежить від того, де на осі часу розміщений цей проміжок (рис. 1.7, в). Характер стаціонарного потоку не повинен змінюватися у часі (тобто інтенсивність стаціонарного потоку постійна (_i = const)). У протилежному випадку потік вимог вважається нестаціонарним.

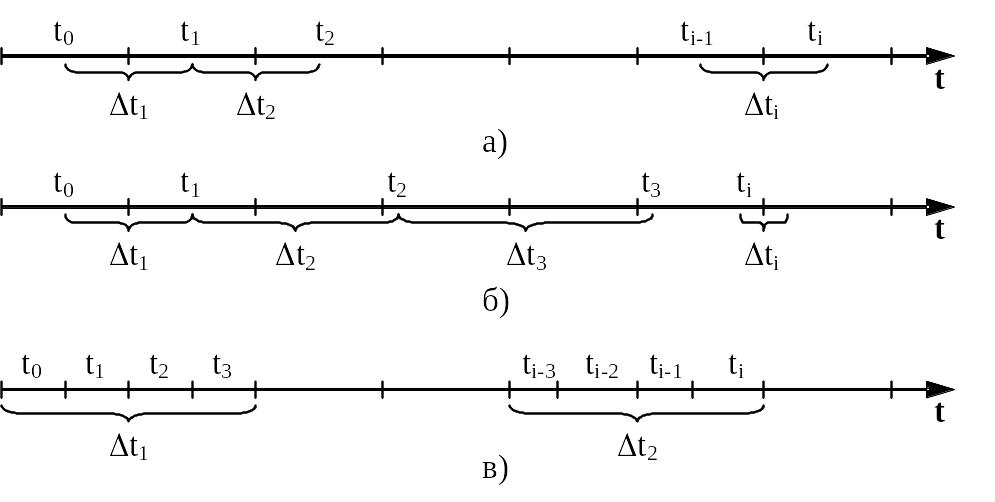
Рис. 1.7. Схематичне зображення моментів надходження вимог у СМО для: а) регулярного потоку; б) випадкового потоку; в) стаціонарного потоку

Випадковий потік вимог називається ординарним, якщо ймовірність попадання на ділянку t двох та більше подій дуже мала порівняно з ймовірністю попадання на цю ділянку однієї події, тобто у будь-який момент часу може з’явитися лише одна вимога. Якщо ж у будь-який момент часу може з’явитися більше однієї вимоги, тоді маємо неординарний або груповий потік вимог.

Потік вимог буде без післядії, якщо для будь-яких інтервалів часу, які не перетинаються, число вимог, що попадає на один з них, не залежатиме від числа вимог, які попадають на інші інтервали. Виконання цієї вимоги означає, що вимоги у СМО надходять незалежно одна від іншої.

На практиці потік вимог об’єктів обслуговування з достатнім набли­женням описується законом розподілу Пуассона

,

де  – інтенсивність потоку вимог, k = 0, 1, 2, ..., t >0, >0.

Покажемо, як під час моделювання СМО можна задати пуасонівський потік вимог. Розглянемо найпростіший потік з інтенсивністю  і позначимо надходження вимоги на осі (0, t), як показано на рис. 1.8.

Рис. 1.8. Моменти надходження вимог для пуасонівського потоку

Визначимо, який розподіл мають проміжки часу Т між сусідніми вимо­гами у потоці. Очевидно, що величина Т буде випадковою. Її інтегральна функція розподілу F(t) = P(T < ) визначає ймовірність того, що величина Т прийме значення, менше за t. Для цього потрібно, щоб на проміжок потра­пила хоча б одна вимога. Обчислимо F(t) через ймовірність протилежної події P₀ того, що за проміжок часу t до системи не надійде жодної події

.

Знаходимо функцію щільності розподілу f(t) випадкової величини Т

.

Отже, щоб отримати пуасонівський потік вхідних вимог, які надходять до системи, достатньо обчислити випадкову величину з експоненціальним розподілом.

Зазначимо, що пуасонівський потік вимог на відміну від найпростішо­го, може бути:

• стаціонарним, якщо інтенсивність  не змінюється у часі;

• нестаціонарним, якщо  залежить від часу,  = (t).

У той же час, найпростіший потік, за визначенням, завжди є стаціонарним.

Пуасонівський закон розподілу не є єдино можливим розподілом опису потоків вимог у СМО. У ряді випадків використовується рівномірний розподіл, розподіл Ерланга та інші розподіли.