9.1. Основні відомості з теорії планування експериментів

9.1.1. Повний факторний експеримент

Теорія планування експериментів розпочалась із роботи знаменитого англійського вченого Р. Фішера в 30-х роках ХХ століття. Вона базується на представленні процесу поведінки систем у вигляді абстрактної схеми „чорного ящика” (рис.9.1), яка описується залежністю

(9.1)

Рис. 9.1. Абстрактна схема системи

Вважається, що у процесі дослідження можна спостерігати вхідні Х=(Х₁,Х₂,...,Х_n) і вихідні Y=(Y₁,Y₂,...,Y_m) змінні. За їх результатами визначається залежність F між входами і виходами моделі. Вхідні змінні будемо називати факторами, а вихідні називаються відгуками. Функція F, яка пов’язує фактори з відгуками, називається функцію відгуку або реакцією системи. Функція G(X) характеризує похибку експеримента та є випадковою величиною. Очевидно, що у загальному випадку Y також є випадковою величиною, оскільки залежить від G(X).

Істинний вигляд функції відгуку F(Х) до експеримента є практично невідомим. Тому для математичного опису функції відгуку використовують поліноми першого, другого або рідше вищих порядків

, (9.2)

де х_і, х_n – змінні фактори.

Рівняння (9.2) є розкладом у ряд Тейлора невідомої функції відгуку в околі точки х_і = х_і0 з коефіцієнтами α₀, α_і, α_іn.

На практиці за результатами експериментів проводиться оброблення даних за допомогою методу найменших квадратів (МНК). Це дозволяє знайти оцінки для відповідних коефіцієнтів α_іn і замінити апроксимуючий поліном (9.2) рівнянням

(9.3)

Рівняння (9.3) називається регресійною моделлю (моделлю регресійного аналізу).

В умовах експерименту фактори можуть варюватися. Цим досягається можливість досліджувати вплив фактора на відгуки моделі. Якщо вплив деякого фактора на спостережувану величину змінюється зі зміною рівня деякого іншого фактора тоді між факторами існує взаємозв’язок. Рівнем фактора називається фіксоване значення фактора в експериментальних дослідженнях. Рівні визначають кількісні значення факторів.

Експеримент, у якому реалізуються всі можливі комбінації рівнів факторів, називається повним факторним експериментом (ПФЕ).

Якщо деякий і-ий фактор має К_і рівнів, то загальне число різних сполучень рівнів у ПФЕ для n факторів знаходиться за формулою

Якщо число рівнів для усіх факторів одинакове, то N=Kⁿ. Кожній комбінації рівнів факторів відповідає одне спостереження. Якщо ж кожний фактор змінюється лише на двох рівнях, то N=2ⁿ.

Застосування ПФЕ замість класичних схем досліджень (в яких змінюється лише один фактор) має ряд суттєвих переваг. Зокрема у ПФЕ аналізується вплив як кожного фактора у різних умовах, так і значна кількість їх комбінацій. Якщо різні фактори, що зумовлюють ефект взаємовпливу не є незалежними, то тільки за допомогою ПФЕ можна аналізувати та прогнозувати цю взаємодію. Для великого класу задач розроблено значну кількість спеціальних факторних планів.

Недоліком ПФЕ є зростання витрат на підготовку і проведення експериментів зі збільшенням кількості факторів та рівнів. Наприклад, побудова регресійної моделі для шести факторів n=6, кожний з яких змінюється на двох рівнях необхідно провести N=2⁶=64 спостережень. Дослідження впливу з десяти факторів (n=10), кожний з яких має k=4 рівні вимагає проведення N=kⁿ=4¹⁰=1048576 cпостережень. Саме вирішення такого класу задач обумовило виникнення теорії планування експеримен­тів – як одного з розділів математичної статистики.

Планом експеримента називається сукупність значень факторів, для яких визначаються значення оцінок функції відгуку, які задовільняють деякому критерію оптимальності.

Побудова регресійної моделі за допомогою повного факторного експеримента складається з таких етапів:

• вибір основних факторів та їх рівнів;

• планування та проведення самого експеримента;

• знаходження коефіцієнтів рівняння регресії (моделі);

• статистичний аналіз результатів експеримента.

У виборі основних факторів враховується їх ранжування за степенем впливу на вихідну величину. Вибір рівнів факторів базується на виконанні двох умов: рівні фактора мають враховувати весь діапазон його зміни; загальна кількість рівнів за всіма факторами не повинна сприяти зростанню великій кількості спостережень. Основною вимогою до діапазону зміни (інтервалу варіювання) і-го фактора ΔX_i є забезпечення виконання умови

,

де S_Xi – середньоквадратичне відхилення фактора,

(X_{i max} – X_{i min}) – область визначення фактора.

Для спрощення запису умов експерименту та оброблення експериментальних даних масштаби за осями координат вибираються так, щоб верхній рівень інтервалу варювання складав +1, а нижній –1.

Для факторів з неперервною областю визначення це досягається за допомогою перетворення (кодування) факторів із натуральної системи координат Х_і до кодованої системи х_і за такими формулами:

. (9.4)

Кодування факторів означає перехід від системи координат у натуральних одиницях до системи координат у кодованій формі (рис. 9.2).

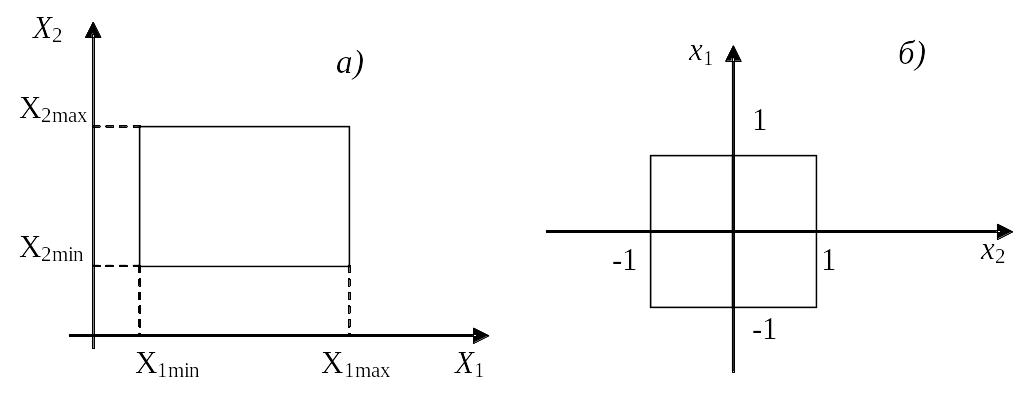
Рис. 9.2. Геометрична інтерпретація плану 2²: а) у натуральних координатах, б) у кодованій формі.

Кожна точка фазового простору – (+1, +1), (–1, +1), (+1, –), (–1, –1) – це спостереження у дослідженнях. План дворівневого факторного експерименту 2² наведено у табл. 9.1 для випадку однакового числа повторювань спостережень у кожному досліді (l – число паралельних дослідів).

Розглянемо алгоритми побудови регресійної моделі за планом ПФЕ 2ⁿ, що описується многочленом першого порядку

(9.5)

Таблиця 9.1

План дворівневого факторного експерименту

Досліди, N	Планування			Результати
	х0	х1	х2
1	+1	+1	+1	y11	y12	…	y1l
2	+1	-1	+1	y21	y22	…	y2l
3	+1	+1	-1	y31	y32	…	y3l
4	+1	-1	-1	y41	y42	…	y4l

Алгоритм реалізується виконанням таких етапів:

• розрахунок коефіцієнтів рівняння регресії (9.5)

; (і = 1, ..., N) , (9.6)

де – середнє значення за паралельними дослідженнями j-го рядка плану ПФЕ (табл. 9.1), N – загальне число дослідів, u – номер паралель­ного досліду, кількість яких становить l;

• оцінка дисперсії відтворюваності (оцінка помилки досліду)

Перед розрахунком помилки досліду необхідно переконатися, що дисперсія дослідів у кожній точці факторного простору не перевищує деякої величини. Для цього розраховуються рядкові дисперсії за формулою

(9.7)

Однорідність дисперсії розраховуємо за критерієм Кохрена. Його розрахункове значення визначається так

, (9.8)

де – максимальна рядкова дисперсія.

Якщо виконується умова

, (9.9)

то гіпотеза про однорідність дисперсій приймається. Табличне значення G_T знаходимо за таблицями (додаток 4 для чисел степенів вільності f₁=l–1, f₂=N та рівня значимості q. Здебільшого використовується 5%-й рівень значимості q=0,05. Якщо умова (9.9) не виконується, то необхідно збільшити число паралельних дослідів.

• перевірка значимості коефіцієнтів регресії використовується для оцінки впливів факторів на відгук регресійної моделі. Для цього знаходимо дисперсію коефіцієнтів регресії (9.5)

, (9.10)

де помилка досліду.

Існують два способи оцінки значимості коефіцієнтів моделі. Перший спосіб полягає у використанні критерію Ст’юдента. Його розрахункове значення обчислюється так

, (9.11)

де – абсолютне значення і-го коефіцієнта регресії. Якщо виконується умова

(9.12)

то і-й коефіцієнт є значимий. Розрахунок значень t_T визначається з таблиць (додаток 4) для відповідних значень f=N(l–1), рівнів значимості q і S_{ai}.

У другому способі використовують довірчий інтервал ∆а_і. Оскільки значення рівні для всіх коефіцієнтів моделі, то ∆а_і є однаковий для всіх а_і

. (9.13)

Значимість коефіцієнтів оцінюють виконанням умови

. (9.14)

Якщо для будь-якого коефіцієнта регресійної моделі (9.4) умови (9.12) або (9.14) не виконуються, то відповідний фактор можна вважати незначним і виключити його з моделі. Але у цьому твердженні потрібно бути обережним, оскільки незначні фактори відсіюються у попередніх експериментах. Більш правильним рішенням є розширення інтервалу варювання для даного фактора і повторення експериментів.

• перевірка адекватності лінійної регресійної моделі здійснюється за критерієм Фішера

, (9.15)

де розрахункове значення критерію Фішера знаходиться за формулами

.

Тут – розрахункове значення відгуку моделі за формулою (9.5), l₁ – число членів у регресійному рівнянні після оцінки значимості. Табличне значення F_T визначається з таблиць (додаток 4 для степеней вільності ) .

Якщо умова (9.15) не виконується, то найчастіше приймають рішення про зменшення інтервалів варювання, повторення експериментів і включення у план експериментів нових факторів, які попередньо не враховувались.

Наведений алгоритм реалізує повний факторний експеримент типу 2ⁿ. ПФЕ є ефективним для отримання математичної моделі досліджуваного об’єкта, особливо для числа факторів n > 3. Однак, збільшення числа факторів зумовлює різке збільшення числа дослідів (N = 2ⁿ), а отже, і зростають машинні витрати і тривалість дослідження.

Як свідчить практика, для отримання необхідних функцій відгуку у випадку, коли дослідника не цікавлять взаємодії високих порядків факторів, можна скористатися деякою частиною (1/2, 1/4, 1/8 і т.д.) усіх можливих комбінацій рівнів факторів від повного факторного експерименту. Такий експеримент називається дробовим факторним експериментом (ДФЕ) [12].

Зменшення числа дослідів не проходить безслідно. З’являються кореля­ції між деякими стовпцями матриці планування експерименту – так звані змішані ефекти. Ця обставина не дозволяє роздільно оцінювати ефекти фак­торів та їх взаємодії. Тому використовувати ДФЕ доцільно для кількості фак­торів n ≥ 5. Для їх побудови використовуються спеціальні алгебраїчні відно­шення, які забезпечують виявлені змішані ефекти. Вони носять назви генеру­ючих відношень [6, 14]. Генеруючі відношення дозволяють встановити не­значні взаємодії, які у матриці планування замінюються новою незалеж­ною змінною. Над генеруючими відношеннями можна здійснювати алгебра­їчні операції. Розрахунок коефіцієнтів регресії та дослідження моделі, отри­ма­ної з використанням ДФЕ, не відрізняється від вище наведеного алгоритму побу­дови регресійної моделі за ПФЕ. Необхідно лише пам’ятати, що обчис­лю­вати можна лише ті коефіцієнти для взаємодіючих факторів, які визнача­ються стовпцями взаємодії, що не співпадають зі стовпцями окремих факторів.