5. Моделювання нормально-розподілених випадкових величин

Нехай потрібно отримати послідовність випадкових чисел, що мають нормальний розподіл

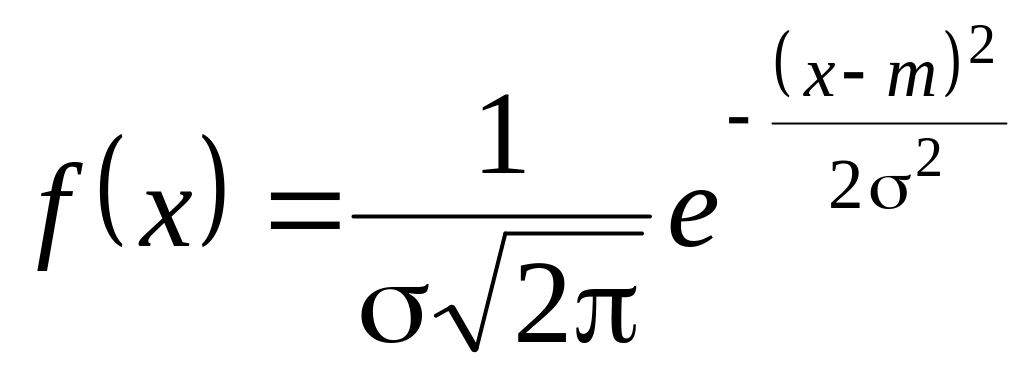, (2.22)

де m, σ – математичне сподівання та середньоарифметичне відхилення.

Надалі випадкові величини, розподілені за нормальним законом, будемо позначати х  N(m, σ). Для моделювання такої випадкової величини не можна безпосередньо скористатися методом оберненої функції, оскільки неможливо аналітично розв’язати рівняння (2.16), бо інтеграл не можна виразити через елементарні функції. Тому для моделювання слід скористатися методом кусково-лінійної апроксимації або методом згорток.

Застосування методу кусково-лінійної апроксимації передбачає отримання випадкових величин х  N(m, σ) у два етапи. На першому етапі здійснюється методом кусково-лінійної апроксимації генерування нормованої нормально-розподіленої випадкової величини х_n (m_xn= 0 і σ_xn= 1).

На другому етапі визначаємо Х за допомогою перетворення

. (2.23)

Щоб одержати на першому етапі х_n  N(0, 1) побудуємо кусково-лінійну апроксимацію функції розподілу

. (2.24)

Тобто, представимо (2.24) у табульованому вигляді (F_i, x_н). Для цього розіб’ємо ординату функції F(x_n) на n ділянок.

Використовуючи методи чисельного інтегрування, визначаємо таку величину x_ni, для якої права частина рівняння (2.24) дорівнюватиме F_i. Використавши цю процедуру для всіх F_i, отримаємо кусково-лінійну апроксимацію (2.24). Тепер можемо використати метод оберненої функції. Якщо r_i потрапляє в інтервал (F_i, F_i-1), то х_n обчислюємо як лінійну інтерполяцію між значеннями оберненої функції у точках і .

На другому етапі обчислюємо значення за формулою (2.23).

Розглянемо застосування методу згорток [4, 12] для моделювання нормально-розподілених випадкових величин. Цей метод базується на центральній граничній теоремі, яка формується таким чином.

Якщо Х₁, ..., Х_n – послідовність незалежних випадкових величин із мате­матичним сподіванням і дисперсією , то у разі необмеженого збільшення значення n функція розподілу випадкової величини

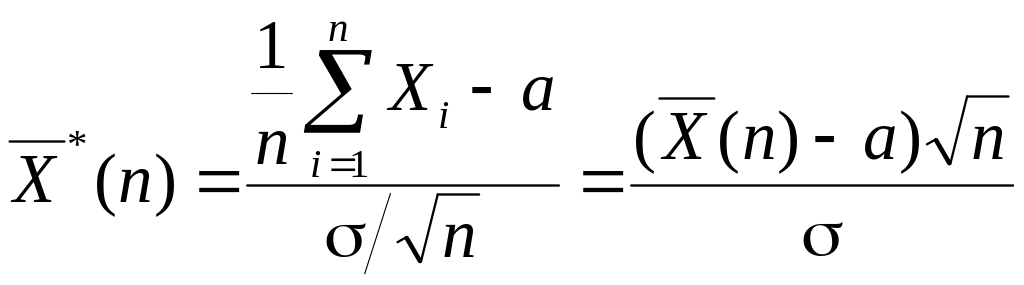
наближається до функції розподілу стандартного нормального закону Ф(z) для усіх значень аргументу, тобто

де , .

Функція Ф(z) називається функцією Лапласа, для значень якої є детальні таблиці.

Алгоритм отримання значень випадкових величин передбачає виконання таких кроків. Спочатку генеруємо послідовність випадкових величин , рівномірно розподілених в інтервалі (0,1). Визначаємо суму . Величина n = 12 є достатнім наближенням до нормально-розподіленої стандартної випадкової величини. Нормальний розподіл з параметрами називається стандартним. Перехід від випадкової величини X_н  N(0,1) до випадкової величини X  N(m,) здійснюється за допомогою перетворення (2.23).

6. Моделювання випадкових векторів

У процесі моделювання систем керування доводиться розглядати сумісно декілька випадкових величин Х₁, Х₂, ..., Х_n. Сукупність таких величин називається векторною (багатовимірною) випадковою величиною або випадковим вектором.

Розглянемо моделювання неперервного випадкового вектора. Якщо усі координати вектора є незалежними випадковими величинами, то за теоремою множення щільності розподілів спільна функція щільності має вигляд

(2.25)

де f_i – функції щільності розподілів величин

У цьому випадку моделювання випадкового вектора зводиться до моделю­вання кожної координати Х_і окремо.

Моделювання неперервного випадкового вектора з залежними складо­вими розглянемо на прикладі вектора з координатами Х₁, Х_2, які описуються функцією щільності f = (Х₁, Х₂). Тоді алгоритм отримання вектора значень неперервної випадкової величини полягає у реалізації таких кроків:

• обчислюємо функцію щільності випадкової величини Х₁

(2.26)

• визначаємо випадкові числа Х₁ відповідно до f₁(x₁) за будь-яким методом, розглянутим у попередньому параграфі;

• вважаючи, що Х = Х₁, знаходимо часткову функцію щільності для другої величини Х₂. Така функція може бути отримана на основі теореми множення законів розподілу

(2.27)

• за допомогою виразу (2.27) для функції щільності можна визначити випадкову величину Х₂ будь-яким методом.

Тоді пара чисел (Х_1і, Х_2і) буде реалізацією неперервного випадкового вектора.

Такий спосіб моделювання двовимірних векторів можна узагальнити і для багатовимірних випадкових векторів. Однак, варто мати на увазі, що обчислення за цим алгоритмом суттєво пов’язане з великими труднощами для n > 2, за виключенням тих рідкісних випадків, коли у явному вигляді можна проінтегрувати функції щільності.

Тому розглянемо інший метод, який дозволяє розв’язати задачу моделювання випадкових векторів, а саме метод розкладання за координатними випадковими величинами.

Нехай багатовимірна випадкова величина (випадковий вектор) з координатами Х_і (і= ) задається математичними сподіваннями m_i = M [X_i] і матрицею кореляційних моментів:

У випадку залежних координат Х_і складові випадкового вектора визначаються у процесі моделювання як лінійне перетворення некорельованих розподілених за нормальним законом нормованих випадкових величин {V₁, V₂, …, V_n}  N(0, 1), m = 0, σ = 1 за такими формулами:

(2.28)

Коефіцієнти перетворення послідовно визначають із співвідношень: