Вариант № 3656584

1. B 9 № 119973. Пря­мая яв­ля­ет­ся ка­са­тель­ной к гра­фи­ку функ­ции . Най­ди­те , учи­ты­вая, что абс­цис­са точки ка­са­ния боль­ше 0.

 

Ре­ше­ние.

Усло­вие ка­са­ния гра­фи­ка функ­ции и пря­мой задаётся си­сте­мой тре­бо­ва­ний:

 

 

В нашем слу­чае имеем:

 

 

По усло­вию абс­цис­са точки ка­са­ния по­ло­жи­тель­на, по­это­му x=0,5, от­ку­да b=−33.

 

Ответ: −33.

Ответ: -33

2. B 9 № 122215.

Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну (где x —рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни t = 3 с.

Ре­ше­ние.

Най­дем закон из­ме­не­ния ско­ро­сти:

.

Тогда на­хо­дим:

 

м/с.

 

Ответ: 3.

Ответ: 3

3. B 9 № 122715.

Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни t = 3 с.

Ре­ше­ние.

Най­дем закон из­ме­не­ния ско­ро­сти:

 

.

 

Тогда на­хо­дим:

м/с.

 

Ответ: 8.

Ответ: 8

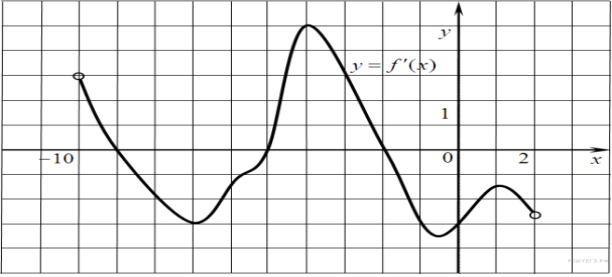
4. B 9 № 27501. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−10; 2). Най­ди­те ко­ли­че­ство точек, в ко­то­рых ка­са­тель­ная к гра­фи­ку функ­ции f(x) па­рал­лель­на пря­мой y = −2x−11 или сов­па­да­ет с ней.

 

Ре­ше­ние.

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной. По­сколь­ку ка­са­тель­ная па­рал­лель­на пря­мой y = −2x−11 или сов­па­да­ет с ней, их уг­ло­вые ко­эф­фи­ци­ен­ты равны –2. Най­дем ко­ли­че­ство точек, в ко­то­рых y'(x₀) = −2, гео­мет­ри­че­ски это со­от­вет­ству­ет ко­ли­че­ству точек пе­ре­се­че­ния гра­фи­ка про­из­вод­ной с пря­мой y = −2. На дан­ном ин­тер­ва­ле таких точек 5.

 

Ответ: 5.

Ответ: 5

5. B 9 № 27494. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−7; 14). Най­ди­те ко­ли­че­ство точек мак­си­му­ма функ­ции f(x) на от­рез­ке [−6; 9].

 

Ре­ше­ние.

Точки мак­си­му­ма со­от­вет­ству­ют точ­кам смены знака про­из­вод­ной с по­ло­жи­тель­но­го на от­ри­ца­тель­ный. На от­рез­ке [−6; 9] функ­ция имеет одну точку мак­си­му­ма x = 7.

 

Ответ: 1.

Ответ: 1

6. B 9 № 119972. Пря­мая яв­ля­ет­ся ка­са­тель­ной к гра­фи­ку функ­ции . Най­ди­те .

 

Ре­ше­ние.

Пря­мая яв­ля­ет­ся ка­са­тель­ной к гра­фи­ку функ­ции в точке тогда и толь­ко тогда, когда од­но­вре­мен­но и . В нашем слу­чае имеем:

 

Ис­ко­мое зна­че­ние а равно 0,125

 

Ответ: 0,125.

При­ве­дем дру­гое ре­ше­ние.

По смыс­лу за­да­чи a ≠ 0, а зна­чит, гра­фик за­дан­ной функ­ции — па­ра­бо­ла. Ка­са­тель­ная к па­ра­бо­ле (а также и к ги­пер­бо­ле) имеет с ней един­ствен­ную общую точку. По­это­му не­об­хо­ди­мо и до­ста­точ­но, чтобы урав­не­ние имело един­ствен­но ре­ше­ние. Для этого дис­кри­ми­нант урав­не­ния дол­жен быть равен нулю, от­ку­да .

Ответ: 0,125

7. B 9 № 123215.

Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни t = 4 с.

Ре­ше­ние.

Най­дем закон из­ме­не­ния ско­ро­сти:

.

Тогда на­хо­дим:

 

м/с.

 

Ответ: 39.

Ответ: 39

8. B 9 № 317542. На ри­сун­ке изоб­ражён гра­фик про­из­вод­ной функ­ции и во­семь точек на оси абс­цисс: , . В сколь­ких из этих точек функ­ция убы­ва­ет?

 

Ре­ше­ние.

Убы­ва­нию диф­фе­рен­ци­ру­е­мой функ­ции со­от­вет­ству­ют от­ри­ца­тель­ные зна­че­ния её про­из­вод­ной. Про­из­вод­ная от­ри­ца­тель­на в точ­ках : точки лежат ниже оси абс­цисс, их ор­ди­на­ты от­ри­ца­тель­гы. Таких точек 5.

 

Ответ: 5.

Ответ: 5

9.B 9 № 27498. 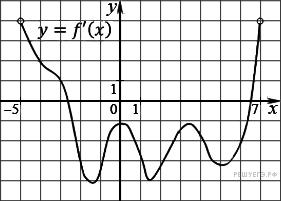На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−5; 7). Най­ди­те про­ме­жут­ки убы­ва­ния функ­ции f(x). В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

 

Ре­ше­ние.

Про­ме­жут­ки убы­ва­ния функ­ции f(x) со­от­вет­ству­ют про­ме­жут­кам, на ко­то­рых про­из­вод­ная функ­ции от­ри­ца­тель­на, то есть ин­тер­ва­лу (−2,5; 6,5). Дан­ный ин­тер­вал со­дер­жит сле­ду­ю­щие целые точки: –2, –1, 0, 1, 2, 3, 4, 5, 6 сумма ко­то­рых равна 18.

 

Ответ: 18.

Ответ: 18

10. B 9 № 27491. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле . В какой точке от­рез­ка функ­ция при­ни­ма­ет наи­боль­шее зна­че­ние?