Вариант № 3700722

1. B 8 . 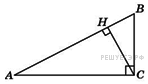В тре­уголь­ни­ке угол равен 90°, – вы­со­та, угол равен , . Най­ди­те .

Ре­ше­ние.

В тре­уголь­ни­ке ABC катет BC лежит на­про­тив угла в 30°, по­это­му он вдвое мень­ше ги­по­те­ну­зы AB: его длина равна 2. В тре­уголь­ни­ке BHC катет BH лежит на­про­тив угла в 30°, по­это­му он вдвое мень­ше ги­по­те­ну­зы BC: его длина равна 1.

Ответ: 1.

Ответ: 1

2. B 8 . В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те .

Ре­ше­ние.

 

.

Ответ: 7.

Ответ: 7

3. B 8 . Пе­ри­метр тра­пе­ции равен 50, а сумма не­па­рал­лель­ных сто­рон равна 20. Най­ди­те сред­нюю линию тра­пе­ции.

Ре­ше­ние.

 

.

Ответ: 15.

Ответ: 15

4. B 8 . В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те вы­со­ту .

Ре­ше­ние.

Углы и равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми. Тогда

 

.

 

 

Ответ: 3,75.

Ответ: 3,75

5. B 8 . В тре­уголь­ни­ке , угол равен . Най­ди­те вы­со­ту .

Ре­ше­ние.

 

.

Ответ: 2.

Ответ: 2

6. B 8 . В тре­уголь­ни­ке угол равен 90°, синус внеш­не­го угла при вер­ши­не равен 0,1. Най­ди­те .

Ре­ше­ние.

так как

,

имеем

Ответ: 0,1.

Ответ: 0,1

7. B 8 . Около окруж­но­сти, ра­ди­ус ко­то­рой равен , опи­сан квад­рат. Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около этого квад­ра­та.

Ре­ше­ние.

Сто­ро­на квад­ра­та вдвое боль­ше ра­ди­у­са впи­сан­ной в него окруж­но­сти. По­это­му Ра­ди­ус опи­сан­ной во­круг квад­ра­та окруж­но­сти равен по­ло­ви­не его диа­го­на­ли. По­это­му

Ответ: 4.

Ответ: 4

8. B 8 . В тре­уголь­ни­ке , вы­со­та равна 4. Най­ди­те .

Ре­ше­ние.

 

.

Ответ: 0,5.

Ответ: 0,5

9. B 8 . 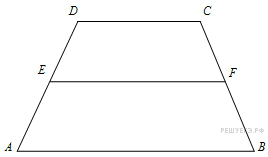Сред­няя линия тра­пе­ции равна 28, а мень­шее ос­но­ва­ние равно 18. Най­ди­те боль­шее ос­но­ва­ние тра­пе­ции.

Ре­ше­ние.

Сред­няя линия равна по­лу­сум­ме ос­но­ва­ний, по­это­му

 

,

от­ку­да

.

 

 

Ответ: 38.

Ответ: 38

10. B 8 . Най­ди­те ги­по­те­ну­зу пря­мо­уголь­но­го тре­уголь­ни­ка, если сто­ро­ны квад­рат­ных кле­ток равны 1.

Вариант № 3700764

1. B 8 . Один угол па­рал­ле­ло­грам­ма боль­ше дру­го­го на . Най­ди­те боль­ший угол. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

сумма углов, при­ле­жа­щих к одной сто­ро­не па­рал­ле­ло­грам­ма равна , а их раз­ни­ца равна .

 

.

Ответ: 125.

 

Ответ: 125

2. B 8 . 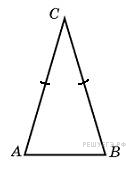Угол при вер­ши­не, про­ти­во­ле­жа­щей ос­но­ва­нию рав­но­бед­рен­но­го тре­уголь­ни­ка, равен 30°. Бо­ко­вая сто­ро­на тре­уголь­ни­ка равна 10. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

Ре­ше­ние.

Пло­щадь тре­уголь­ни­ка равна по­ло­ви­не про­из­ве­де­ния его сто­рон на синус угла между ними. По­это­му

 

см².

Ответ: 25.

Ответ: 25

3. B 8 . В тре­уголь­ни­ке угол равен 90°, – вы­со­та, , . Най­ди­те .

Ре­ше­ние.

Углы и равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми.

 

.

Ответ: 17,5.

Ответ: 17,5

4. B 8 .

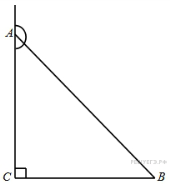
В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те ко­си­нус внеш­не­го угла при вер­ши­не .

Ре­ше­ние.

так как

Ответ: –0,28.

Ответ: -0,28

5. B 8 . В тре­уголь­ни­ке угол равен 90°,. Най­ди­те ко­си­нус внеш­не­го угла при вер­ши­не .

Ре­ше­ние.

так как

Ответ: –0,96.

Ответ: -0,96

6. B 8 . В тре­уголь­ни­ке , . Най­ди­те .

Ре­ше­ние.

Тре­уголь­ник рав­но­бед­рен­ный, зна­чит, вы­со­та делит ос­но­ва­ние по­по­лам.

 

.

Ответ: 8.

Ответ: 8

7. B 8 .

В тре­уголь­ни­ке угол равен 90°, Най­ди­те

Ре­ше­ние.

Имеем:

Ответ: 0,25.

Ответ: 0,25

8. B 8 .

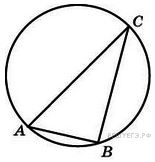Угол тре­уголь­ни­ка , впи­сан­но­го в окруж­ность ра­ди­у­са 3, равен . Най­ди­те сто­ро­ну этого тре­уголь­ни­ка.

Ре­ше­ние.

 

Ответ: 3.

Ответ: 3

9. B 8 . Мень­шая сто­ро­на пря­мо­уголь­ни­ка равна 6, диа­го­на­ли пе­ре­се­ка­ют­ся под углом . Най­ди­те диа­го­на­ли пря­мо­уголь­ни­ка.

Ре­ше­ние.

и , зна­чит, тре­уголь­ник – рав­но­сто­рон­ний.

 

.

Ответ: 12.

Ответ: 12

10. B 8 . В тре­уголь­ни­ке , вы­со­та равна 7, . Най­ди­те .

Ре­ше­ние.

Тре­уголь­ник рав­но­бед­рен­ный, зна­чит, вы­со­та делит ос­но­ва­ние по­по­лам.

 

.

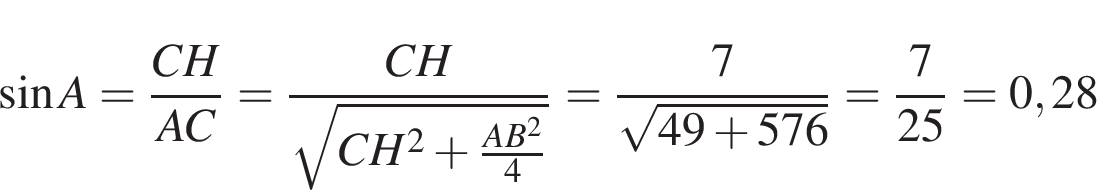Ответ: 0,28.

Ответ: 0,28

Ре­ше­ние.

по тео­ре­ме Пи­фа­го­ра:

 

.

Ответ: 5.

Ответ: 5

Ре­ше­ние.

Вы­ра­зим пло­щадь тре­уголь­ни­ка двумя спо­со­ба­ми:

 

  .

От­сю­да имеем:

Ответ: 0,5.

Ответ: 0,5

Ре­ше­ние.

так как

Ответ: –0,1.

Ответ: -0,1

Ре­ше­ние.

так как

Ответ: 0,5.

Ответ: 0,5

Ре­ше­ние.

Углы и равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми.

 

.

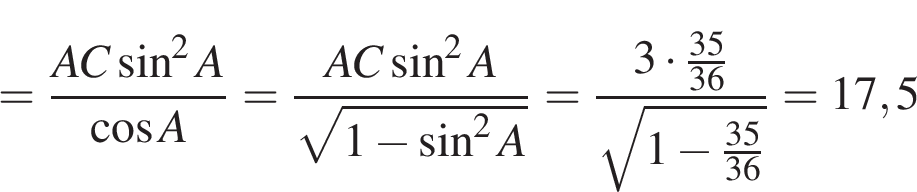Ответ: 17,5.

Ответ: 17,5

Ре­ше­ние.

 

Ответ: -0,4.

Ответ: -0,4

Ре­ше­ние.

Пло­щадь па­рал­ле­ло­грам­ма равна про­из­ве­де­нию его ос­но­ва­ния на вы­со­ту, опу­щен­ную на это ос­но­ва­ние. Пусть вы­со­ты равны со­от­вет­ствен­но a и b. Тогда S = 5   a = 10   b = 40. По­это­му a = 8, b = 4. Боль­шая вы­со­та равна 8.

 

Ответ: 8.

Ответ: 8

Ре­ше­ние.

 

Ответ: -0,4.

Ответ: -0,4

Ре­ше­ние.

Угол между ка­са­тель­ной и хор­дой равен по­ло­ви­не за­клю­чен­ной между ними дуги. В тре­уголь­ни­ке

 

Ответ: 118.

 

Ответ: 118