Вариант № 3700527

1. B 8 . Най­ди­те сто­ро­ну пра­виль­но­го ше­сти­уголь­ни­ка, опи­сан­но­го около окруж­но­сти, ра­ди­ус ко­то­рой равен .

Ре­ше­ние.

Рас­смот­рим рав­но­сто­рон­ной тре­уголь­ник AOB (см. рис.). В этом тре­уголь­ни­ке

 

 

Ответ: 2.

Ответ: 2

2. B 8 .

В тре­уголь­ни­ке угол равен 90°, . Най­ди­те тан­генс внеш­не­го угла при вер­ши­не .

Ре­ше­ние.

так как

Ответ: –0,1.

Ответ: -0,1

3. B 8 . Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма, если два его угла от­но­сят­ся как . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

сумма углов, при­ле­жа­щих к одной сто­ро­не па­рал­ле­ло­грам­ма равна . Тогда

 

.

Ответ: 126.

 

Ответ: 126

4. B 8 . Сто­ро­на ту­по­уголь­но­го тре­уголь­ни­ка равна ра­ди­у­су опи­сан­ной около него окруж­но­сти. Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

 

;

Ответ: 150.

Ответ: 150

5. B 8 . Най­ди­те ко­си­нус угла . В от­ве­те ука­жи­те зна­че­ние ко­си­ну­са, умно­жен­ное на .

Ре­ше­ние.

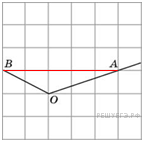до­стро­им угол до тре­уголь­ни­ка . Из ри­сун­ка на­хо­дим , , . Вос­поль­зу­ем­ся тео­ре­мой ко­си­ну­сов:

 

.

Тогда:

.

Ответ: -2.

 

Ответ: -2

6. B 8 . В тре­уголь­ни­ке угол равен 90°, Най­ди­те

Ре­ше­ние.

Имеем:

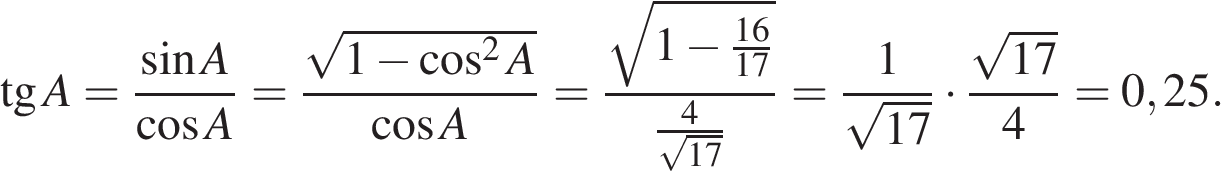
Ответ: 0,25.

Ответ: 0,25

7. B 8 . В тре­уголь­ни­ке , вы­со­та равна 4, . Най­ди­те .

Ре­ше­ние.

Тре­уголь­ник рав­но­бед­рен­ный, зна­чит, углы и равны как углы при его осо­ва­нии.

 

.

Ответ: 0,5.

Ответ: 0,5

8. B 8 . В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те .

Ре­ше­ние.

 

Ответ: 8.

Ответ: 8

9. B 8 . Че­ты­рех­уголь­ник впи­сан в окруж­ность. Угол равен , угол равен . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

впи­сан­ный угол равен по­ло­ви­не дуги, на ко­то­рую он опи­ра­ет­ся, зна­чит

 

Ответ: 70.

Ответ: 70

10. B 8 .

В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те тан­генс внеш­не­го угла при вер­ши­не .

Ре­ше­ние.

так как

Ответ: –0,25.

Ответ: -0,25

Вариант № 3700572

1. B 8 . В тре­уголь­ни­ке , вы­со­та равна 4, угол равен . Най­ди­те .

Ре­ше­ние.

 

.

Ответ: 8.

Ответ: 8

2. B 8 .

В тре­уголь­ни­ке угол равен 90°, тан­генс внеш­не­го угла при вер­ши­не равен , . Най­ди­те .

Ре­ше­ние.

так как

.

Ответ: 7.

Ответ: 7

3. B 8 .

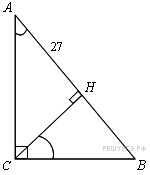
В тре­уголь­ни­ке угол равен 90°,  — вы­со­та, , . Най­ди­те .Ре­ше­ние.

Углы и равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми. По­это­му из тре­уголь­ни­ков BHC и BCA имеем:

 

 

 

Ответ: 12.

Ответ: 12

4. B 8 . В тре­уголь­ни­ке , . Най­ди­те тан­генс внеш­не­го угла при вер­ши­не .

Ре­ше­ние.

так как

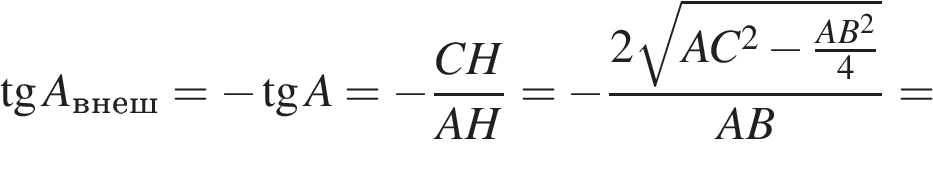
Ответ: –0,25.

Ответ: -0,25

5. B 8 .

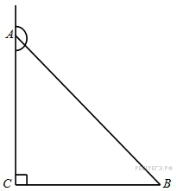
В тре­уголь­ни­ке угол равен 90°, тан­генс внеш­не­го угла при вер­ши­не равен , . Най­ди­те .

Ре­ше­ние.

 

.

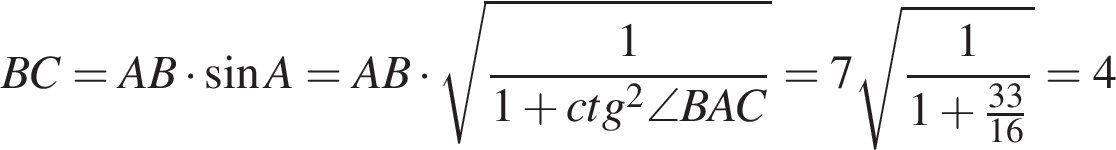Ответ: 4.

Ответ: 4

6. B 8 .

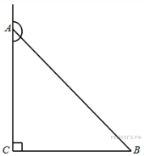
В тре­уголь­ни­ке угол равен 90°, ко­си­нус внеш­не­го угла при вер­ши­не равен –0,6, . Най­ди­те .

Ре­ше­ние.

так как

Ответ: 25.

Ответ: 25

7. B 8 . В тре­уголь­ни­ке , – вы­со­та, . Най­ди­те .

Ре­ше­ние.

Тре­уголь­ник рав­но­бед­рен­ный, зна­чит, углы и равны как углы при его ос­но­ва­нии.

 

.

Ответ: 0,1.

Ответ: 0,1

8. B 8 .

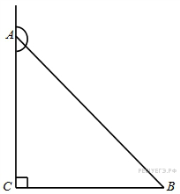
В тре­уголь­ни­ке угол равен 90°, ко­си­нус внеш­не­го угла при вер­ши­не равен , . Най­ди­те .

Ре­ше­ние.

так как

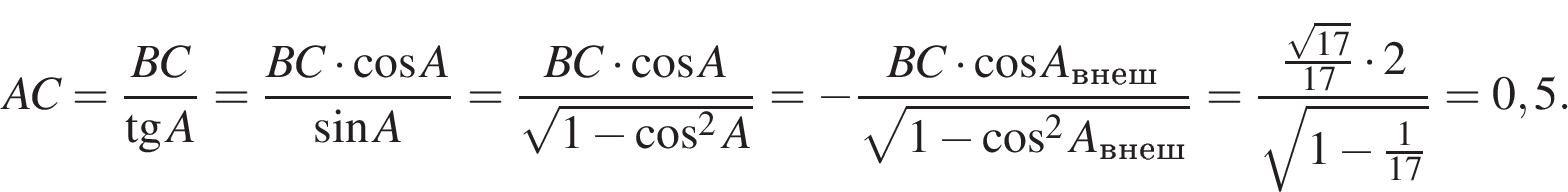
Ответ: 0,5.

Ответ: 0,5

9. B 8 . В тре­уголь­ни­ке , . Най­ди­те ко­си­нус внеш­не­го угла при вер­ши­не .

Ре­ше­ние.

 

Ответ: .

Ответ: -0,5

10. B 8 . В тре­уголь­ни­ке угол равен 90°, тан­генс внеш­не­го угла при вер­ши­не равен . Най­ди­те .

Ре­ше­ние.

Най­дем ко­си­нус внеш­не­го угла:

 

Тогда

 

 

Ответ: 0,28.

Ответ: 0,28