
- •Вариант № 3672485
- •Вариант № 3686886
- •Вариант № 3686988
- •6. B 8 . В треугольнике угол равен 90°, . Найдите косинус внешнего угла при вершине .
- •Вариант № 3687023
- •Вариант № 3687088
- •Вариант № 3687122
- •Вариант № 3687180
- •Вариант № 3700400
- •Вариант № 3700450
- •Вариант № 3700527
- •Вариант № 3700572
- •Вариант № 3700630
- •Вариант № 3700688
- •Вариант № 3700722
- •Вариант № 3700764
Вариант № 3700450
1. B 8 . Найдите высоту ромба, сторона которого равна , а острый угол равен .
Решение.
.
Ответ: 1,5.
Ответ: 1,5
2. B 8 . Угол равен . Его сторона касается окружности. Найдите градусную величину большей дуги окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Решение.
Касательная к окружности перпендикулярна радиусу, центральный угол равен дуге, на которую он опирается, значит, треугольник – прямоугольный и
Ответ: 114.
Ответ: 114
3.
B 8 .
В треугольнике
угол
равен
90°,
![]() .
Найдите
.
.
Найдите
.
Решение.
![]()
Ответ: 0,1.
Ответ: 0,1
4. B 8 .
В треугольнике угол равен 90°, тангенс внешнего угла при вершине равен , . Найдите .
Решение.
так как
.
Ответ: 7.
Ответ: 7
5. B 8 . Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда
![]() ,
,
отсюда
![]() .
Высота в трапеции отсекает
прямоугольный треугольник.
Высота в прямоугольном
треугольнике является
катетом и равна половине
гипотенузы, соответственно
угол напротив высоты равен
30°.
.
Высота в трапеции отсекает
прямоугольный треугольник.
Высота в прямоугольном
треугольнике является
катетом и равна половине
гипотенузы, соответственно
угол напротив высоты равен
30°.
Ответ: 30.
Примечание.
Внимательный читатель заметит, что на рисунке изображена равнобедренная трапеция, а в условии описана неравнобедренная. Действительно, если бы боковые стороны были равны друг другу, то сумма длин меньшего основания и двух боковых сторон трапеции оказалась бы меньше длины большего основания, а это невозможно. С другой стороны, в тексте условия не сказано, что трапеция является равнобедренной, а слова «найдите угол, прилежащий к данной боковой стороне» говорят о том, что боковые стороны могут быть разными.
Ответ: 30
6.
B 8 .
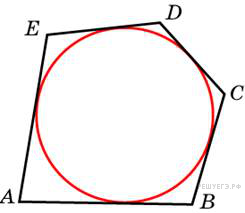 Около
окружности, радиус которой
равен 3, описан многоугольник,
периметр которого равен
20. Найдите его площадь.
Около
окружности, радиус которой
равен 3, описан многоугольник,
периметр которого равен
20. Найдите его площадь.
Решение.
Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру. Пусть площадь равна S, периметр равен P, радиус окружности равен R. Тогда
![]() .
.
Поэтому S = 30.
Ответ: 30.
Ответ: 30
7.
B 8 .
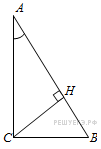 В
треугольнике
угол
равен
90°,
–
высота,
В
треугольнике
угол
равен
90°,
–
высота,
![]() ,
.
Найдите
.
,
.
Найдите
.
Решение.
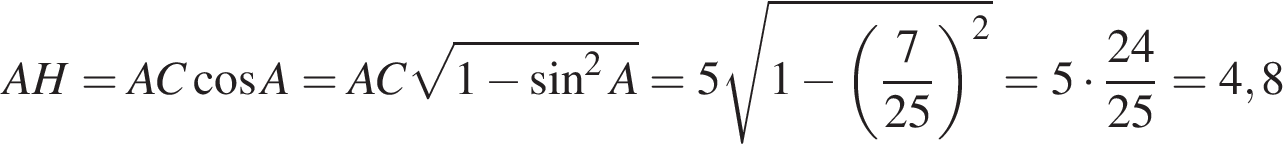 .
.
Ответ: 4,8.
Ответ: 4,8
8.
B 8 .
 Один
угол равнобедренного
треугольника на 90° больше
другого. Найдите меньший
угол. Ответ дайте в градусах.
Один
угол равнобедренного
треугольника на 90° больше
другого. Найдите меньший
угол. Ответ дайте в градусах.
Решение.
так
как треугольник равнобедренный,
то углы при его основании равны.
Обозначим за меньший угол,
тогда больший угол равен
![]() .
Имеем
.
Имеем
![]() .
.
Ответ: 30.
Ответ: 30
9.
B 8 .
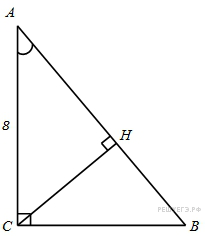
В
треугольнике
угол
равен
90°,
![]() ,
,
![]() .
Найдите высоту
.
.
Найдите высоту
.
Решение.
Рассмотрим прямоугольный треугольник AHC. В нём
![]()
Ответ: 4.
Ответ: 4
10.
B 8 .
В
треугольнике
,
угол
равен
,
![]() .
Найдите
.
.
Найдите
.
Решение.
воспользуемся теоремой косинусов:
![]() ,
,
Тогда
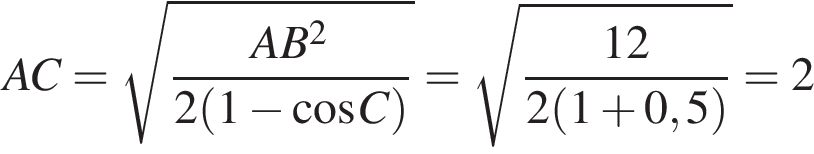 .
.
Ответ: 2.
Ответ: 2
