Вариант № 3687180

1. B 8 .

В тре­уголь­ни­ке угол равен 90°, синус внеш­не­го угла при вер­ши­не равен , . Най­ди­те .

Ре­ше­ние.

так как

Ответ: 4,8.

Ответ: 4,8

2. B 8 .

В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те синус внеш­не­го угла при вер­ши­не .

Ре­ше­ние.

так как

Ответ: 0,28.

Ответ: 0,28

3. B 8 . В тре­уголь­ни­ке угол равен 90°, . Най­ди­те .

Ре­ше­ние.

 

Ответ: 0,25.

Ответ: 0, 25

4. B 8 . В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те .

Ре­ше­ние.

Найдём по сле­ду­ю­щей фор­му­ле:

.

Ответ: 8.

Ответ: 8

5. B 8 . В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те .

Ре­ше­ние.

 

.

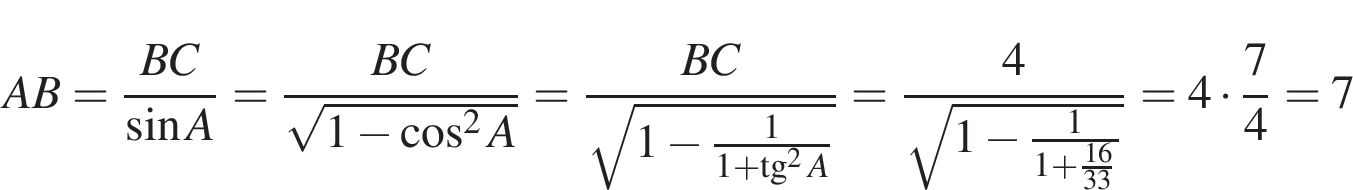Ответ: 7.

Ответ: 7

6. B 8 . В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те .

Ре­ше­ние.

 

Ответ: 4.

Ответ: 4

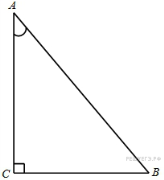
7. B 8 . В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те .

Ре­ше­ние.

 

.

Ответ: 0,28.

Ответ: 0,28

8. B 8 . 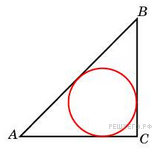Ра­ди­ус окруж­но­сти, впи­сан­ной в рав­но­бед­рен­ный пря­мо­уголь­ный тре­уголь­ник, равен 2. Най­ди­те ги­по­те­ну­зу этого тре­уголь­ни­ка. В от­ве­те ука­жи­те .

Ре­ше­ние.

Пусть длина ка­те­тов равна , тогда длина ги­по­те­ну­зы равна , а ра­ди­ус впи­сан­ной окруж­но­сти, вы­чис­ля­е­мый по фор­му­ле , равен

 

.

По усло­вию , от­ку­да

 

.

 

Тре­бо­ва­лось найти , имеем:

 

.

 

 

Ответ: 4.

Ответ: 4

9. B 8 . В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те .

Ре­ше­ние.

 

.

Ответ: 0,5.

Ответ: 0,5

10. B 8 . В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те .

Ре­ше­ние.

 

.

Ответ: 0,5.

Ответ: 0,5

Вариант № 3700400

1. B 8 . Най­ди­те вы­со­ту ромба, сто­ро­на ко­то­ро­го равна , а ост­рый угол равен .

Ре­ше­ние.

 

.

Ответ: 1,5.

Ответ: 1,5

2. B 8 . В тре­уголь­ни­ке , – вы­со­та, , . Най­ди­те .

Ре­ше­ние.

Тре­уголь­ник рав­но­бед­рен­ный, зна­чит, углы и равны как углы при его осо­ва­нии.

 

.

Ответ: 0,6.

Ответ: 0,6

3. B 8 . В тре­уголь­ни­ке , вы­со­та равна 7, . Най­ди­те .

Ре­ше­ние.

Тре­уголь­ник рав­но­бед­рен­ный, зна­чит, углы и равны как углы при его ос­но­ва­нии.

 

.

Ответ: 0,28.

Ответ: 0,28

4. B 8 . В тре­уголь­ни­ке угол равен 90°, – вы­со­та, , . Най­ди­те .

Ре­ше­ние.

 

.

Ответ: 17,5.

Ответ: 17,5

5. B 8 . В тре­уголь­ни­ке , угол равен 90°. Ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка равен 5. Най­ди­те .

Ре­ше­ние.

Ги­по­те­ну­за пря­мо­уголь­но­го тре­уголь­ни­ка яв­ля­ет­ся диа­мет­ром опи­сан­ной во­круг него окруж­но­сти, по­это­му ее длина 10. Тогда по тео­ре­ме Пи­фа­го­ра:

 

Ответ: 8.

Ответ: 8

6. B 8 . Най­ди­те сто­ро­ну пра­виль­но­го ше­сти­уголь­ни­ка, опи­сан­но­го около окруж­но­сти, ра­ди­ус ко­то­рой равен .

Ре­ше­ние.

Рас­смот­рим рав­но­сто­рон­ной тре­уголь­ник AOB (см. рис.). В этом тре­уголь­ни­ке

 

 

Ответ: 2.

Ответ: 2

7. B 8 . Ги­по­те­ну­за пря­мо­уголь­но­го тре­уголь­ни­ка равна 26. Один из его ка­те­тов равен 10. Най­ди­те дру­гой катет.

Ре­ше­ние.

по тео­ре­ме Пи­фа­го­ра:

 

.

Ответ: 24.

Ответ: 24

8. B 8 .

В тре­уголь­ни­ке угол равен 90°, синус внеш­не­го угла при вер­ши­не равен 0,5, . Най­ди­те .

Ре­ше­ние.

так как

Ответ: 8.

Ответ: 8

9. B 8 . В тре­уголь­ни­ке угол равен 90°, – вы­со­та, , . Най­ди­те .

Ре­ше­ние.

Углы и равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми.

 

.

Ответ: 17,5.

Ответ: 17,5

10. B 8 . В тре­уголь­ни­ке угол равен 90°, . Най­ди­те .