Задание В8.

Вариант № 3672485

1. B 8 . Най­ди­те диа­го­наль пря­мо­уголь­ни­ка, впи­сан­но­го в окруж­ность, ра­ди­ус ко­то­рой равен 5.

Ре­ше­ние.

угол яв­ля­ет­ся пря­мым, он опи­ра­ет­ся на диа­го­наль ко­то­рая яв­ля­ет­ся диа­мет­ром.

 

Ответ: 10.

Ответ: 10

2. B 8 . В тре­уголь­ни­ке , , синус внеш­не­го угла при вер­ши­не равен 0,6. Най­ди­те .

Ре­ше­ние.

так как

Ответ: 25.

Ответ: 25

3. B 8 .

В тре­уголь­ни­ке угол равен 90°, – вы­со­та, , . Най­ди­те .

Ре­ше­ние.

Углы и равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми.

 

.

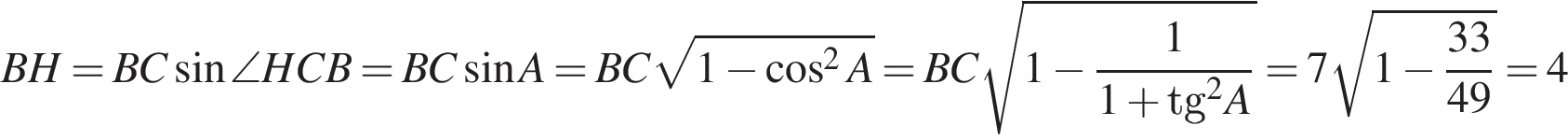Ответ: 4.

Ответ: 4

4. B 8

 . В тре­уголь­ни­ке угол равен 90°, вы­со­та равна 7, . Най­ди­те .

Ре­ше­ние.

Углы и равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми.

 

.

Ответ: 0,28.

Ответ: 0,28

5. B 8 . 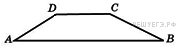Ос­но­ва­ния тра­пе­ции равны 18 и 6, бо­ко­вая сто­ро­на, рав­ная 7, об­ра­зу­ет с одним из ос­но­ва­ний тра­пе­ции угол 150°. Най­ди­те пло­щадь тра­пе­ции.

Ре­ше­ние.

 

.

Ответ: 42.

Ответ: 42

6. B 8 . 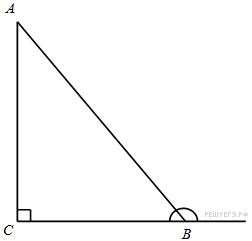В тре­уголь­ни­ке угол равен 90°, . Най­ди­те ко­си­нус внеш­не­го угла при вер­ши­не .

Ре­ше­ние.

так как

,

имеем

Ответ: –0,96.

Ответ: -0,96

7. B 8 . В тре­уголь­ни­ке угол равен 90°,  — вы­со­та, , . Най­ди­те .

 

 

Ре­ше­ние.

Углы и равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми.

 

.

Ответ: 0,5

Ответ: 0,5

8. B 8

  Ра­ди­ус окруж­но­сти равен 1. Най­ди­те ве­ли­чи­ну ту­по­го впи­сан­но­го угла, опи­ра­ю­ще­го­ся на хорду, рав­ную . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

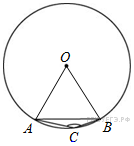впи­сан­ный угол до­пол­ня­ет по­ло­ви­ну цен­траль­но­го угла, опи­ра­ю­ще­го­ся на ту же хорду, до .

 

,

зна­чит, , .

Ответ: 135.

Ответ: 135

9. B 8 .

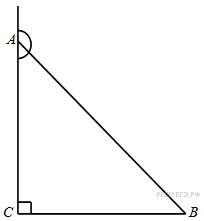
В тре­уголь­ни­ке угол равен 90°, тан­генс внеш­не­го угла при вер­ши­не равен -0,5, . Най­ди­те .

Ре­ше­ние.

так как

Ответ: 8.

Ответ: 8

10. B 8 . 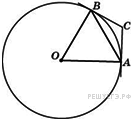Через концы , дуги окруж­но­сти в про­ве­де­ны ка­са­тель­ные и . Най­ди­те угол . Ответ дайте в гра­ду­сах.

Вариант № 3686886

1. B 8 .

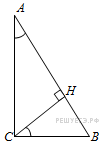В тре­уголь­ни­ке угол равен 90°, , . Най­ди­те вы­со­ту .

Ре­ше­ние.

Углы и равны как углы со вза­им­но пер­пен­ди­ку­ляр­ны­ми сто­ро­на­ми.

 

.

Ответ: 3,75.

Ответ: 3,75

2. B 8 . Сто­ро­на пра­виль­но­го тре­уголь­ни­ка равна . Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в этот тре­уголь­ник.

Ре­ше­ние.

Ра­ди­ус впи­сан­ной в тре­уголь­ник окруж­но­сти равен от­но­ше­нию пло­ща­ди к по­лу­пе­ри­мет­ру:

Ответ: 0,5.

 

При­ме­ча­ние

Дру­гой спо­соб ре­ше­ния со­сто­ит в ис­поль­зо­ва­нии фор­му­лы, вы­ра­жа­ю­щей ра­ди­ус впи­сан­ной в рав­но­сто­рон­ний тре­уголь­ник через его сто­ро­ну: .

Ответ: 0,5

3. B 8 .

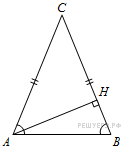В тре­уголь­ни­ке , – вы­со­та, . Най­ди­те .

Ре­ше­ние.

Тре­уголь­ник рав­но­бед­рен­ный, зна­чит, углы и равны как углы при его ос­но­ва­нии.

 

.

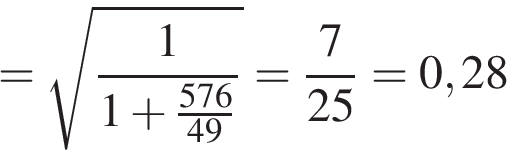Ответ: 0,28.

Ответ: 0,28

4. B 8 .

В тре­уголь­ни­ке , , . Най­ди­те вы­со­ту .

Ре­ше­ние.

Тре­уголь­ник рав­но­бед­рен­ный, зна­чит, вы­со­та делит ос­но­ва­ние по­по­лам.

 

.

Ответ: 4.

Ответ: 4

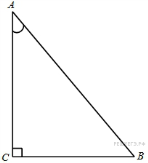
5. B 8 . В тре­уголь­ни­ке угол равен 90°, . Най­ди­те .

Ре­ше­ние.

 

.

Ответ: 0,28.

Ответ: 0,28

6. B 8 .

Най­ди­те диа­го­наль пря­мо­уголь­ни­ка, впи­сан­но­го в окруж­ность, ра­ди­ус ко­то­рой равен 5.

Ре­ше­ние.

угол яв­ля­ет­ся пря­мым, он опи­ра­ет­ся на диа­го­наль ко­то­рая яв­ля­ет­ся диа­мет­ром.

 

Ответ: 10.

Ответ: 10

7. B 8 .

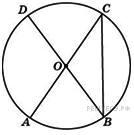В окруж­но­сти с цен­тром и – диа­мет­ры. Цен­траль­ный угол равен . Най­ди­те впи­сан­ный угол . Ответ дайте в гра­ду­сах.

Ре­ше­ние.

впи­сан­ный угол равен по­ло­ви­не цен­траль­но­го угла, опи­ра­ю­ще­го­ся на ту же дугу окруж­но­сти, зна­чит

 

Ответ: 35.

Ответ: 35

8. B 8 . Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 4 и 12.

Ре­ше­ние.

Пло­щадь ромба равна по­ло­ви­не про­из­ве­де­ния его диа­го­на­лей. По­это­му

 

.

Ответ: 24.

Ответ: 24

9. B 8 .

В тре­уголь­ни­ке угол равен 90°, синус внеш­не­го угла при вер­ши­не равен . Най­ди­те .

Ре­ше­ние.

так как

Ответ: 0,25.

Ответ: 0,25

10. B 8 . В па­рал­ле­ло­грам­ме . Най­ди­те