Вариант № 3670876

1. B 7 . Най­ди­те ко­рень урав­не­ния .

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

Ответ: −1.

Ответ: -1

2. B 7 . Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: 5.

Ответ: 5

3. B 7 . Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те мень­ший из кор­ней.

 

Ре­ше­ние.

Пе­ре­ве­дем число в пра­вой части урав­не­ния в не­пра­виль­ную дробь и умно­жим обе части урав­не­ния на 3, по­лу­ча­ем:

 

Ответ:  −7.

Ответ: -7

4. B 7 . Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

 

Ре­ше­ние.

За­ме­тим, что чис­ли­те­ли дро­бей равны. Имеем:

Ответ: 1.

Ответ: 1

5. B 7 . Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

Ре­ше­ние.

За­ме­тим, что чис­ли­те­ли дро­бей равны. Имеем:

Ответ: 6.

Ответ: 6

6. B 7 . Най­ди­те ко­рень урав­не­ния .

Ре­ше­ние.

Пе­рей­дем к од­но­му ос­но­ва­нию сте­пе­ни:

.

Ответ: 10.

Ответ: 10

7. B 7 . Ре­ши­те урав­не­ние .

Ре­ше­ние.

Воз­ве­дем в квад­рат:

Ответ:  −2,5.

Ответ: -2,5

8. B 7 . Най­ди­те ко­рень урав­не­ния:

Ре­ше­ние.

Воз­ве­дем в квад­рат:

Ответ: −5.

Ответ: -5

9. B 7 . Най­ди­те ко­рень урав­не­ния .

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: −4.

Ответ: -4

10. B 7 . Ре­ши­те урав­не­ние . В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.

Вариант № 3670954

1. B 7 . Най­ди­те ко­рень урав­не­ния

Ре­ше­ние.

Из­вле­кая ко­рень пятой сте­пе­ни из обеих ча­стей урав­не­ния, по­лу­ча­ем , от­ку­да .

Ответ: 0

2. B 7 . Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те мень­ший из кор­ней.

Ре­ше­ние.

Воз­ве­дем в квад­рат:

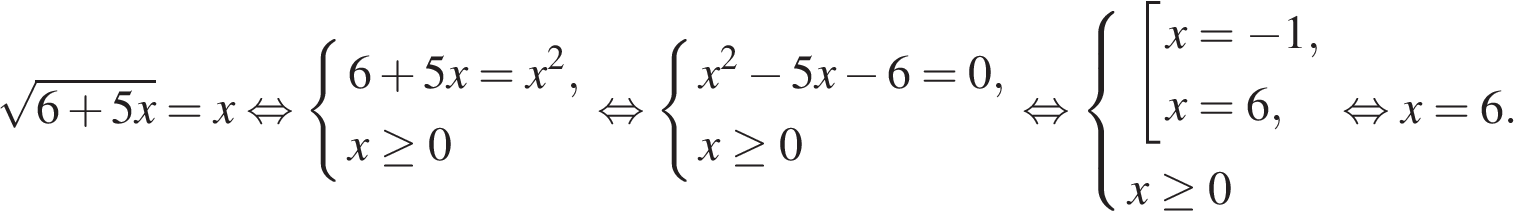
Урав­не­ние имеет един­ствен­ный ко­рень, он и яв­ля­ет­ся от­ве­том.

 

Ответ: 6.

 

При­ме­ча­ние.

Можно было сде­лать про­вер­ку. Под­став­ляя число 6, по­лу­ча­ем вер­ное ра­вен­ство , по­это­му число 6 яв­ля­ет­ся кор­нем. Под­став­ляя число −1, по­лу­ча­ем не­вер­ное ра­вен­ство , по­это­му число −1 не яв­ля­ет­ся кор­нем.

Ответ: 6

3. B 7 . Най­ди­те ко­рень урав­не­ния .

Ре­ше­ние.

Ло­га­риф­мы двух вы­ра­же­ний равны, если сами вы­ра­же­ния равны и при этом по­ло­жи­тель­ны:

 

 

 

Ответ: 6.

Ответ: 6

4. B 7 . Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

Ответ: 5.

Ответ: 5

5. B 7 . Най­ди­те ко­рень урав­не­ния .

Ре­ше­ние.

Воз­ве­дем в квад­рат:

Ответ: 55.

Ответ: 55

6. B 7 . Най­ди­те ко­рень урав­не­ния: .

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­ча­ем:

.

Ответ: 0,3.

Ответ: 0,3

7. B 7 . Ре­ши­те урав­не­ние . В от­ве­те на­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.

Ре­ше­ние.

Решим урав­не­ние:

Зна­че­нию со­от­вет­ству­ет . По­ло­жи­тель­ным зна­че­ни­ям па­ра­мет­ра со­от­вет­ству­ют по­ло­жи­тель­ные зна­че­ния кор­ней, от­ри­ца­тель­ным зна­че­ни­ям па­ра­мет­ра со­от­вет­ству­ют мень­шие зна­че­ния кор­ней. Сле­до­ва­тель­но, наи­боль­шим от­ри­ца­тель­ным кор­нем яв­ля­ет­ся число −1.

Ответ:  −1.

Ответ: -1

8. B 7 . Ре­ши­те урав­не­ние . Если урав­не­ние имеет более од­но­го корня, в от­ве­те ука­жи­те мень­ший из них.

Ре­ше­ние.

На ОДЗ пе­рей­дем к урав­не­нию на ос­но­ва­ние ло­га­риф­ма:

 

 

Итак, на ОДЗ урав­не­ние имеет толь­ко один ко­рень.

 

Ответ: 12.

Ответ: 12

9. B 7 . Ре­ши­те урав­не­ние . В от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень.

Ре­ше­ние.

По­сле­до­ва­тель­но по­лу­чим:

Зна­че­ни­ям со­от­вет­ству­ют по­ло­жи­тель­ные корни.

Если , то .

Если , то .

Зна­че­ни­ям со­от­вет­ству­ют мень­шие зна­че­ния кор­ней.

Сле­до­ва­тель­но, наи­мень­шим по­ло­жи­тель­ным кор­нем яв­ля­ет­ся число .

 

Ответ:  1.

Ответ: 1

10. B 7 . Най­ди­те корни урав­не­ния: В ответ за­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.