23.2. Критическая область. Область принятия гипотезы. Критические точки

Для проверки нулевой гипотезы используют специально подобранную случайную величину, распределение которой известно. Обозначим эту величину .

Определение. Статистическим критерием называют случайную величину , которая служит для проверки нулевой гипотезы.

Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают частное (наблюдаемое) значение критерия.

Определение. Наблюдаемым значением называют значение критерия, вычисленное по выборкам.

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая – при которых она принимается.

Определение. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают, а совокупность значений критерия, при которых гипотезу принимают, называют областью принятия гипотезы.

Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то гипотезу отвергают, а если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.

Критическая область и область принятия гипотезы, это есть некоторые интервалы, следовательно, существуют точки, которые их разделяют.

Определение. Критическими точками (границами) называют точки, отделяющие критическую область от области принятия гипотезы.

Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.

Правосторонней называют критическую область, определяемую неравенством , где - положительное число.

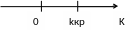
Левосторонней называют критическую область, определяемую неравенством , где - отрицательное число.

Двусторонней называют критическую область, определяемую неравенствами 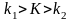, где .

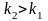В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами 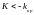и или равносильным неравенством .

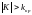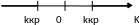
Для отыскания правосторонней или левосторонней критической области, необходимо найти критическую точку . Для ее нахождения задаются достаточно малой вероятностью- уровнем значимости . Затем находят критическую точку , исходя из требований

(для правосторонней области)

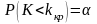(для левосторонней области.).

Двусторонняя критическая область определяется неравенствами . Поэтому, критические точки находят исходя из требований

.

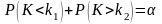Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этим требованиям.

После того, как критическая точка найдена, вычисляют по данным выборок наблюдаемое значение критерия , и если выполняется неравенство , то нулевую гипотезу отвергают; если же , то нет оснований, чтобы отвергнуть нулевую гипотезу.

Наряду с уровнем значимости , то есть вероятностью того, что будет отвергнута правильная гипотеза, рассматривают вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза. Эту вероятность называют мощностью критерия.