Глава 22. Статистические оценки параметров распределения
22.1. Оценки параметров распределения признака
Пусть требуется изучить количественный признак X генеральной совокупности. Предполагается, что из теоретических соображений известно, какой именно вид имеет распределение признака X, однако неизвестно значение некоторого параметра θ, характеризующего это распределение (например, это параметр λ в распределении Пуассона, или параметр p в биномиальном распределении). Обычно в распоряжении исследователя имеются лишь данные выборки, т.е. значения количественного признака x1, x2,..., xn полученные в результате n независимых наблюдений. Через эти данные и выражают оцениваемый параметр. Значения x1, x2,..., xn можно рассматривать как реализации n независимых случайных величин X1, X2 ..., Xn, каждая из которых имеет тот же закон распределения, что и сама случайная величина X.
Определение. Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.
Для того, чтобы статистические оценки давали «хорошее» приближение оцениваемых параметров, они должны удовлетворять определенным требованиям.
Определение. Оценка
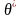называется несмещенной если ее
математическое ожидание равно
оцениваемому параметру
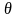при любом объеме выборки, то есть
.
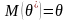Определение. Несмещенная оценка называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра θ, вычисленных по выборкам одного и того же объема n.
Определение. Оценка называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:
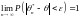для любого
.
В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности и эффективности. Однако иногда для простоты расчетов целесообразно применять оценки, обладающие большей дисперсией по сравнению с эффективными оценками, или незначительно смещенные оценки и т.п.
22.2. Понятия генеральной и выборочной средней. Формулы вычисления
Пусть изучается дискретная
генеральная совокупность относительно
количественного признака
.
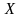Определение. Генеральной
средней
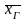называют среднее арифметическое
значений признака генеральной
совокупности. В случае бесконечной
генеральной совокупности под генеральной
средней понимается математическое
ожидание распределения признака X.
Пусть для изучения генеральной совокупности относительно количественного признака произведена выборка объема .
Определение.
Выборочной средней
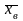называют среднее арифметическое значений
выборочной совокупности.
Если все значения
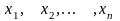признака выборочной совокупности объема
различны, то
.
Если же значения признака
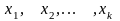имеют соответственно частоты
,
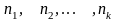причем
,
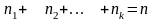то
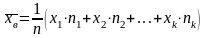
или
.
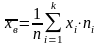Выборочная средняя, является несмещенной и состоятельной оценкой генеральной средней.
22.3. Понятия генеральной и выборочной дисперсий и формулы вычисления
В качестве характеристики разброса значений количественного признака X вокруг своего среднего значения используется дисперсия.
Определение.
Генеральной дисперсией
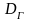называют средне арифметическое квадратов
отклонений значений признака генеральной
совокупности от их среднего значения
.
Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются числовой характеристикой, называемой средним квадратическим отклонением.
Определение. Генеральным средним квадратическим отклонением называют корень квадратный из генеральной дисперсии и обозначают в виде
Пусть для изучения генеральной совокупности относительно количественного признака произведена выборка объема .
Определение.
Выборочной дисперсией
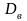называется среднее арифметическое
квадратов отклонений наблюдаемых
значений выборки от выборочной средней
.
Если все значения признака выборки объема различны, то
.
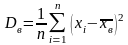Если же значения признака имеют соответственно частоты , причем , то
.
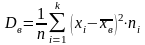Определение. Выборочным средним квадратическим отклонением называют корень квадратный из выборочной дисперсии и обозначают в виде
.
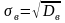Записанные выше формулы вычисления выборочной и генеральной дисперсии можно упрости, используя следующую теорему.
Теорема. Дисперсия равна разности между средним квадратов значений признака и квадратом общей средней, то есть
,
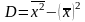где
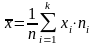и
.
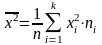Пример. Выборочная совокупность задана таблицей распределения
-
1
2
3
4
20
15
10
5
Найти выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение.
Решение.
Найдем выборочную среднюю.
.
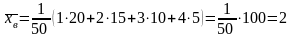Найти выборочную дисперсию.
.
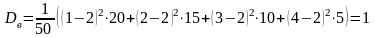Общая средняя уже известна
.
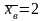Найдем среднюю квадратов значений признака:
.
Тогда
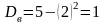и
-
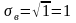это среднее отклонение от среднего
значения выборки, то есть от числа
.
Если в качестве оценки
генеральной дисперсии использовать
выборочную дисперсию, то эта оценка
будет приводить к систематическим
ошибкам, давая заниженное значение
генеральной дисперсии. Объясняется это
тем, что выборочная дисперсия является
смещенной оценкой генеральной дисперсии,
т.е.
Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия
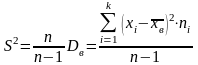
Обе предложенные оценки - выборочная дисперсия и исправленная выборочная дисперсия – являются состоятельными оценками генеральной дисперсии, и разница между ними заметна лишь при небольшом числе наблюдений n. При n > 30 в качестве оценки для D вполне можно использовать Dв. В случае нормально распределенной генеральной совокупности обе эти оценки также являются асимптотически эффективными, т.е. при n→∞ они будут стремиться к эффективной оценке.
Для оценки же среднего квадратического отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно корню квадратному из исправленной дисперсии и обозначается в виде
.
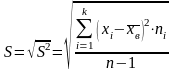Пример. Найти выборочную и исправленную дисперсии для следующего статистического распределения
-
1
2
5
8
9
3
4
6
4
3
Решение.
Найдем выборочную среднюю.
.
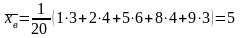Найдем выборочную дисперсию по определению.
.
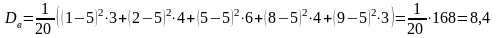Тогда
.
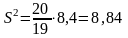