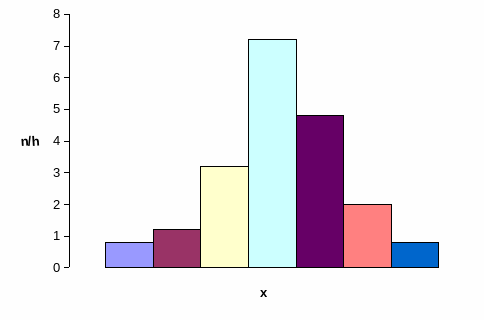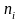21. 2. Статистическое распределение выборки.

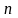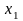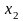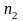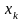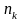Пусть из генеральной совокупности извлечена выборка объема . Причем объект наблюдался раз; - раз;… - раз.

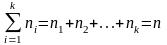- объем выборки.

Определение. Наблюдаемые значения 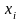называются вариантами, а последовательность вариант записанных в возрастающем порядке – вариационным рядом.

Определение. Числа наблюдений n₁, n₂,… n_k- называются частотами.

Определение. Отношение частоты к объему выборки называют относительной частотой.

Обозначается: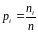

Замечание: Сумма относительных частот равна 1.

Изучение выборки начинают с составления статистического распределения – таблицы с двумя строками. В одной строке указывается значения признака, в другой – соответствующие им частоты.

Определение. Статистическим распределением выборки называют таблицу значений признака расположенных в возрастающем порядке, и соответствующих им частот или относительных частот.

Различают два вида статистических распределений:

а) статистическое распределение выборки, представленное в виде таблицы, в первой строке которой перечислены все возможные варианты, а во второй – соответствующие им частоты называют дискретным вариационным рядом;

б) статистическое распределение выборки, представленное в виде таблицы, в первой строке которой находится последовательность интервалов а во второй – соответствующая частота, равная сумме всех частот вариант, попавших в данный интервал, называется интервальным вариационным рядом.

Составление статистического распределения начинают с определения наименьшего и наибольшего значений признака. Остальные записывают между ними в порядке возрастания. Далее подсчитывают частоты каждого значения признака.

Для непрерывно варьирующего количественного признака интервал его изменения разбивают на частичные интервалы одинаковой длины.

21.3. Графическое изображение статистического распределения выборки и эмпирической функции распределения.

Статистическое распределение выборки изображается графически в виде полигона и гистограммы.

Определение. Полигон, как правило, служит для изображения дискретного вариационного ряда, и представляет собой ломаную, отрезки которой соединяют точки

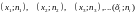
Для построения полигона частот на оси абсцисс откладывают значения вариант х_i, а на оси ординат - соответствующие им частоты n_i. Точки 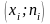соединяют отрезками прямых и получают полигон частот.

Замечание. Аналогично строится полигон относительных частот, отмечаются точки с координатами 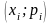и соединяются прямыми линиями.

Например. По данному распределению выборки построить полигон частот.

	1	2	3	5
	4	2	3	1

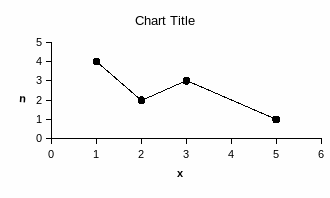
Полигоном обычно пользуются в случае небольшого числа вариант. В случае большого числа вариант и в случае непрерывного распределения признака чаще строят гистограмму. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длинной 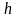и находят для каждого частичного интервала сумму частот вариант попавших в 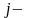ый интервал. Затем, на этих интервалах, как на основаниях, строят прямоугольники с высото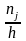й или .

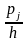Определение. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению , которое называют плотностью частоты.

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки параллельные оси абсцисс на расстоянии .

Площадь 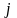-го частичного прямоугольника равна , то есть сумме частот вариант - го интервала. Площадь всей гистограммы частот равна сумме всех частот, т.е, объему выборки.

Например. Построить гистограмму частот по следующим данным

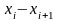
	5-10	10-15	15-20	20-25	25-30	30-35	35-40
	4	6	16	36	24	10	4
	0,8	1,2	3,2	7,2	4,8	2	0,8