
- •Раздел X. Случайные величины
- •Глава 19. Дискретная случайная величина
- •19.1. Основные понятия случайных величин
- •19.2. Числовые характеристики дискретной случайной величины
- •Свойства математического ожидания
- •2. Дисперсия дискретной случайной величины
- •Свойства дисперсии
- •В частности, из свойств дисперсии следует, что
- •Примеры решения типовых задач
- •Найдем ее математическое ожидание, дисперсию и среднеквадратичное отклонение. Решение:
- •Раздел XI.Выборочный метод
- •Глава 21. Выборочный метод
- •21.1. Генеральная и выборочная совокупности. Виды выборки
- •21. 2. Статистическое распределение выборки.
- •21.3. Графическое изображение статистического распределения выборки и эмпирической функции распределения.
- •Глава 22. Статистические оценки параметров распределения
- •22.1. Оценки параметров распределения признака
- •22.2. Понятия генеральной и выборочной средней. Формулы вычисления
- •22.3. Понятия генеральной и выборочной дисперсий и формулы вычисления
- •22.4. Точность оценки, доверительная вероятность (надежность). Доверительный интервал.
- •Раздел XII. Статистическая проверка статистических гипотез
- •Глава 23. Проверка гипотез
- •23.1. Понятие статистической гипотезы
- •23.2. Критическая область. Область принятия гипотезы. Критические точки
- •23.3. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
- •23.5. Методика вычисления теоретических частот нормального распределения
- •Пример решения типовой задачи
- •Контрольный тест после изучения разделов XI, XII «Статистическая проверка статистических гипотез»
- •Раздел XIII.Элементы теории корреляции
- •Глава 24. Элементы корреляционного анализа
- •24.1. Основные понятия корреляционного анализа.
- •24.2. Корреляционная таблица и корреляционное поле
- •24.3. Выборочное уравнение регрессии
- •24.4. Выборочный коэффициент корреляции
- •24.5. Оценка тесноты любой связи
- •Свойства корреляционных отношений
- •Пример решения типовой задачи
- •Контрольный тест после изучения раздела XIII «Элементы теории корреляции»
- •Задачи для контрольной работы № 4
- •Элементы математической статистики
- •Контрольные вопросы к итоговой аттестации по предмету
24.5. Оценка тесноты любой связи
Как рассматривалось выше, оценка тесноты линейной связи осуществляется с помощью выборочного коэффициента корреляции. Но связь между признаками и не всегда является линейной. Рассмотрим, как оценить тесноту любой корреляционной связи, как линейной, так и нелинейной.
Пусть данные наблюдений над количественными признаками и сведены в корреляционной таблице. Эти данные можно разбить на группы, причем каждая группа будет содержать те значения , которые соответствуют определенному значению .
Пример. Пусть дана следующая корреляционная таблица
-
x
y
2
3
5
ny
25
20
20
45
30
1
31
110
1
48
49
nx
20
31
49
100
Данные этой таблиц можно разбить на группы относительно признаков и . Рассмотрим группы по признаку .
К первой группе относится 20
значений
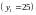 ,
которые соответствуют
,
которые соответствуют
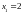 .
.
Ко второй группе относится
31 значений
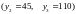 ,
которые соответствуют
,
которые соответствуют
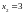 .
.
К третей группе относится 49
значений
,
которые соответствуют
 .
.
Таким образом, в данном случае, все исходные значения по признаку , можно разбить на три группы и вычислить групповые средние, которые совпадают с условными средними:
; ; .
Аналогично, можно разбить данные по признаку так же на три группы и найти групповые средние , получим
; ; .
После разбиения данных на группы и вычисления групповых средних можно вычислить средние квадратические отклонения условных средних и по формулам
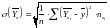 ,
,
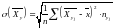 .
.
С помощью этих средних квадратических отклонений, вычисляют корреляционные отношения по и по , по формулам
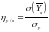 и
и
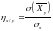 ,
,
где - среднее квадратическое отклонение признака ;
- среднее квадратическое отклонение признака .
По приведенным корреляционным отношениям определяют тесноту любой связи, как линейной, так и нелинейной.
Свойства корреляционных отношений
Корреляционное отношение удовлетворяет двойному неравенству
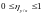 и
и
 .
.
Если
 и
и
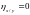 ,
то признаки
и
не связаны между собой корреляционной
зависимостью.
,
то признаки
и
не связаны между собой корреляционной
зависимостью.
Если корреляционное отношение
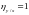 ,
то между признаками
и
существует функциональная зависимость.
,
то между признаками
и
существует функциональная зависимость.
Выборочный коэффициент линейной корреляции по абсолютной величине не больше корреляционных отношений, то есть
 и
и
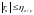 .
.
Если
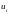 - это условные варианты признака
,
и
- это условные варианты признака
,
и
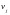 - это условные варианты признака
,
то
- это условные варианты признака
,
то
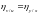 и
и
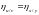 .
.
Как показывает первое свойство, корреляционное отношение может принимать значения из промежутка от 0 до 1, причем, чем ближе значение корреляционного отношения к 1, тем теснее связь между рассматриваемыми признаками, и чем ближе это значение к 0, тем слабее связь между рассматриваемыми признаками.
Замечание: Как было сказано выше, корреляционное отношение служит мерой тесноты любой связи, в том числе и линейной формы. В этом состоит преимущество корреляционного отношения. Но так же оно имеет и недостатки: а) оно определяют только тесноту связи, но не указывают на направление связи, так как они вычисляются с помощью средних квадратических отклонений, которые всегда положительны; б) оно не позволяет судить на сколько близко расположены точки, найденные по данным наблюдений, к кривой определенного вида, например к параболе, гиперболе и т.д. Это объясняется тем, что при определении корреляционного отношения форма связи во внимание не принимается.
Пример. Распределение признаков и приведено в следующей корреляционной таблице
X Y |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
ny |
-2 |
|
|
|
1 |
2 |
1 |
|
|
|
4 |
-1 |
|
|
1 |
3 |
|
3 |
1 |
|
|
8 |
0 |
|
2 |
4 |
|
|
|
4 |
2 |
|
12 |
1 |
1 |
5 |
|
|
|
|
|
5 |
1 |
12 |
2 |
3 |
|
|
|
|
|
|
|
3 |
6 |
nx |
4 |
7 |
5 |
4 |
2 |
4 |
5 |
7 |
4 |
42 |
Найти корреляционные отношения
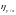 и
и
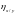 ,
и сравнить их с соответствующим
коэффициентом линейной корреляции.
,
и сравнить их с соответствующим
коэффициентом линейной корреляции.
Решение.
Найдем групповые средние:
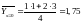 ;
;
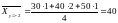 ;
;
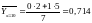 ;
;
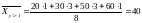 ;
;
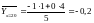 ;
;
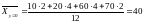 ;
;
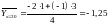 ;
;
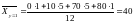 ;
;
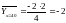 ;
;
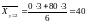 .
.
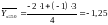 ;
;
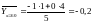 ;
;
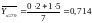 ;
;
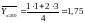 .
.
Для вычисления общих средних построим расчетные таблицы.
|
|
|
|
|
|
0 |
4 |
0 |
0 |
1,75 |
0 |
10 |
7 |
70 |
700 |
0,714 |
50 |
20 |
5 |
100 |
2000 |
-0,2 |
-20 |
30 |
4 |
120 |
3600 |
-1,25 |
-150 |
40 |
2 |
80 |
3200 |
-2 |
-160 |
50 |
4 |
200 |
10000 |
-1,25 |
-250 |
60 |
5 |
300 |
18000 |
-0,2 |
-60 |
70 |
7 |
490 |
34300 |
0,714 |
350 |
80 |
4 |
320 |
25600 |
1,75 |
560 |
∑ |
42 |
1680 |
97400 |
- |
320 |
|
|
|
|
|
|
-2 |
4 |
-8 |
16 |
40 |
-320 |
-1 |
8 |
-8 |
8 |
40 |
-320 |
0 |
12 |
0 |
0 |
40 |
0 |
1 |
12 |
12 |
12 |
40 |
480 |
2 |
6 |
12 |
24 |
40 |
480 |
∑ |
42 |
8 |
60 |
- |
320 |
Тогда:
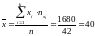 ;
;
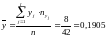 ;
;
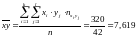 ;
;
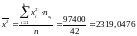 ;
;
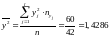 ;
;
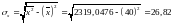 ;
;
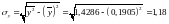 .
.
 ,
следовательно, линейной связи между
признаками
и
нет.
,
следовательно, линейной связи между
признаками
и
нет.
Для нахождения корреляционных отношений найдем средние квадратические отклонения для условных средних и по формулам
, .
Получим
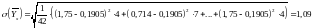 ;
;
 .
.
Тогда
 ;
;
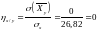 .
.
Корреляционное отношение
 показывает, что признак
зависит от влияния признака
,
а отношение
показывает, что признак
не зависит от влияния признака
.
показывает, что признак
зависит от влияния признака
,
а отношение
показывает, что признак
не зависит от влияния признака
.
