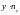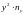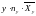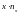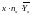- •Раздел X. Случайные величины
- •Глава 19. Дискретная случайная величина
- •19.1. Основные понятия случайных величин
- •19.2. Числовые характеристики дискретной случайной величины
- •Свойства математического ожидания
- •2. Дисперсия дискретной случайной величины
- •Свойства дисперсии
- •В частности, из свойств дисперсии следует, что
- •Примеры решения типовых задач
- •Найдем ее математическое ожидание, дисперсию и среднеквадратичное отклонение. Решение:
- •Раздел XI.Выборочный метод
- •Глава 21. Выборочный метод
- •21.1. Генеральная и выборочная совокупности. Виды выборки
- •21. 2. Статистическое распределение выборки.
- •21.3. Графическое изображение статистического распределения выборки и эмпирической функции распределения.
- •Глава 22. Статистические оценки параметров распределения
- •22.1. Оценки параметров распределения признака
- •22.2. Понятия генеральной и выборочной средней. Формулы вычисления
- •22.3. Понятия генеральной и выборочной дисперсий и формулы вычисления
- •22.4. Точность оценки, доверительная вероятность (надежность). Доверительный интервал.
- •Раздел XII. Статистическая проверка статистических гипотез
- •Глава 23. Проверка гипотез
- •23.1. Понятие статистической гипотезы
- •23.2. Критическая область. Область принятия гипотезы. Критические точки
- •23.3. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
- •23.5. Методика вычисления теоретических частот нормального распределения
- •Пример решения типовой задачи
- •Контрольный тест после изучения разделов XI, XII «Статистическая проверка статистических гипотез»
- •Раздел XIII.Элементы теории корреляции
- •Глава 24. Элементы корреляционного анализа
- •24.1. Основные понятия корреляционного анализа.
- •24.2. Корреляционная таблица и корреляционное поле
- •24.3. Выборочное уравнение регрессии
- •24.4. Выборочный коэффициент корреляции
- •24.5. Оценка тесноты любой связи
- •Свойства корреляционных отношений
- •Пример решения типовой задачи
- •Контрольный тест после изучения раздела XIII «Элементы теории корреляции»
- •Задачи для контрольной работы № 4
- •Элементы математической статистики
- •Контрольные вопросы к итоговой аттестации по предмету
24.3. Выборочное уравнение регрессии
Если изучаются две случайные величины и , заданные парами значений , причем такие, что связь между ними предположительно можно считать линейной, то задача в установлении формы связи решается путем составления линейных уравнений, называемых уравнениями линейной регрессии. Эти уравнения записывают в следующем виде:
 - уравнение линейной регрессии
на
,
- уравнение линейной регрессии
на
,
 - уравнение линейной регрессии
на
,
- уравнение линейной регрессии
на
,
где
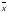 - среднее значение наблюдаемых значений
с.в.
;
- среднее значение наблюдаемых значений
с.в.
;
 - среднее значение наблюдаемых значений
с.в.
;
- среднее значение наблюдаемых значений
с.в.
;
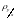 - коэффициент линейной регрессии
на
;
- коэффициент линейной регрессии
на
;
 - коэффициент линейной регрессии
на
.
- коэффициент линейной регрессии
на
.
Приведенные величины вычисляются по следующим формулам:
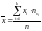 ;
;
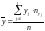 ;
;
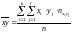 ;
;
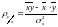 ;
;
 ,
,
где
 - среднее квадратическое отклонение
с.в.
;
- среднее квадратическое отклонение
с.в.
;
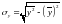 - среднее квадратическое отклонение
с.в.
;
- среднее квадратическое отклонение
с.в.
;
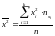 ,
,
 .
.
Найденные уравнения регрессии преобразуют к виду
 - уравнение линейной регрессии у
на х,
- уравнение линейной регрессии у
на х,
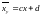 - уравнение линейной регрессии х на
у.
- уравнение линейной регрессии х на
у.
Коэффициент линейной регрессии у на х, то есть , показывает, на сколько единиц своего измерения в среднем изменится значение признака , если значение признака увеличить на единицу его измерения.
Коэффициент линейной регрессии х на у, то есть , показывает, на сколько единиц в среднем изменится значение признака при изменении признака на единицу его измерения.
Пример. Данные об объеме выпуска продукции в тыс. штук (Y) и стоимости основных промышленных фондов в млн. руб. (X) по 60 предприятиям сгруппированы в таблице. Вычислить коэффициенты линейной регрессии и составить уравнение Y на X.
-
x
y
1
3
5
7
9
ny
0,1
2
2
4
0,3
2
7
10
19
0,5
2
17
7
26
0,7
4
3
2
9
0,9
2
2
nx
4
11
31
10
4
60
Решение. Найдем условные средние по формулам
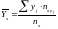 и
и
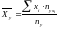 .
.
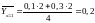 ;
;
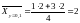 ;
;
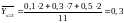 ;
;
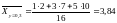 ;
;
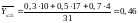 ;
;
 ;
;
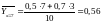 ;
;
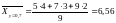 ;
;
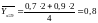 ;
;
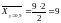 .
.
Для удобства вычислений составим расчетные таблицы.
|
|
|
|
|
|
0,1 |
4 |
0,4 |
0,04 |
2 |
0,8 |
0,3 |
19 |
5,7 |
1,71 |
3,84 |
21,89 |
0,5 |
26 |
13 |
6,5 |
5,38 |
69,94 |
0,7 |
9 |
6,3 |
4,41 |
6,56 |
41,33 |
0,9 |
2 |
1,8 |
1,62 |
9 |
16,2 |
∑ |
60 |
27,2 |
14,28 |
- |
150,16 |
|
|
|
|
|
|
1 |
4 |
4 |
4 |
0,2 |
0,8 |
3 |
11 |
33 |
99 |
0,3 |
9,9 |
5 |
31 |
155 |
775 |
0,46 |
71,3 |
7 |
10 |
70 |
490 |
0,56 |
39,2 |
9 |
4 |
36 |
324 |
0,8 |
28,8 |
∑ |
60 |
298 |
1692 |
- |
150 |
Тогда
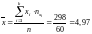 ;
;
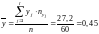 ;
;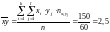 ;
;
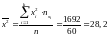 ;
;
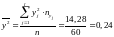 ;
;
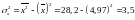 ;
;
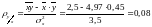 ;
;
Тогда уравнение линейной регрессии на , будет иметь вид
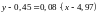 ,
,
или
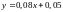 .
.
Это уравнение показывает, что при увеличении стоимости основных производственных фондов на 1 млн. руб., выпуск продукции увеличится в среднем на 0,08 тыс. штук.