Раздел X. Случайные величины

Глава 19. Дискретная случайная величина

19.1. Основные понятия случайных величин

Определение. Случайной называется величина, которая в результате испытания принимает одно и только одно возможное значение, какое именно заранее неизвестно.

Случайные величины делятся на дискретные и непрерывные.

Определение. Случайная величина называется дискретной, если в результате испытания она принимает одно из значений х₁, х₂, х₃, … , х_n, … с соответствующей вероятностью р₁, р₂, … , р_n, …

Определение. Непрерывной называется случайная величина, которая может принимать любое значение из некоторого промежутка.

Например, число студентов на лекции – дискретная случайная величина, продолжительность лекции – непрерывная.

Закон распределения дискретной случайной величины

Соответствие между возможными значениями х_k случайной величины Х и их вероятностями р_k называется законом распределения вероятностей дискретной случайной величины Х.

Закон распределения обычно задается таблицей:

Возможные значения случайной величины Х	х1	х2	…	хn
Вероятности этих значений Р	р1	р2	…	рn

То, что случайная величина Х принимает одно из значений х₁, х₂, … , х_n, есть достоверное событие и поэтому должно выполняться равенство (в случае бесконечной последовательности значений ).

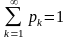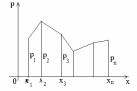
Закон распределения может быть задан графически в виде многоугольника распределения вероятностей, т.е. в виде ломаной, соединяющей точки (х_k, р_k).

Примеры.

1. Переменная величина Х есть число очков, выпадающее на верхней грани игральной кости при ее однократном бросании. Составить закон распределения этой случайной величины.

Решение.

Так как любое число очков при однократном бросании кости выпадает с вероятностью 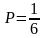, то закон распределения случайной величины имеет вид:

Х	1	2	3	4	5	6
р	1/6	1/6	1/6	1/6	1/6	1/6

2. Вероятность попадания при каждом выстреле р=0,8. Имеется три снаряда. Определить вероятность того, что будет израсходован один снаряд, два снаряда, три снаряда, если стрельба ведется до первого попадания или промаха всеми тремя снарядами. Составить таблицу распределения случайной величины Х – числа израсходованных снарядов.

Решение.

Пусть Х – число израсходованных снарядов. Обозначим 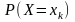- вероятность того, что будет израсходовано х_k снарядов.

Тогда Р(х=1)=0,8, Р(х=2)=(1-р)р=0,16, Р(х=3)=(1-р)²=0,04.

Таблица распределения будет иметь вид

Х	1	2	3
р		0,16	0,04

3. Экзаменатор задал студенту 4 дополнительных вопроса. Вероятность того, что студент ответит на любой заданный вопрос 0,9. Составить закон распределения случайной величины Х – числа ответов на заданные вопросы.

Решение.

Используем формулу Бернулли 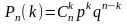. Здесь n=4, р=0,9, q=0,1.

,

,

,

,

.

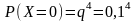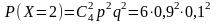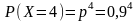Х	0	1	2	3	4
Р	0,0001	0,0036	0,0486	0,2916	0,6561