1 Вариант

Вынести общий множитель за скобки: 6x⁸-9x⁶+3x⁵; 6a²b+8ab³-12a²b²; 7x(2x-y)+y(y-2x); (n+m)²-2n(n+m); (x-3)²+(3-x); (3x-9)(x+2)-(3-x)(x+5).

Разложить на множители методом группировки: ab+2b-3a-6; 2x²+4ax+5x+10a; x²-6x+8;

Вычислить рациональным способом: 2,017·3,56+0,483·0,44+2,017·0,44+0,483·3,56

Решить уравнение: 3x(2x-7)-(x+1)(7-2x) = 0.

Сумма двух чисел равна 20. Если первое число увеличить на 4, а второе уменьшить на 2, то их произведение уменьшится на 12. Найти эти числа.

2 Вариант

Вынести общий множитель за скобки: 6x⁸-10x⁵-2x³; 6a²b⁴+9ab³-12a²b²; 5x(2x-3y)-y²(3y-2x); (n-m)²+2m(n-m); (x-y)²+(y-x); (3x-9)(x+2)-(6-2x)(x+1).

Разложить на множители методом группировки: ab+5b+3a+15; 2x²-6ax-3x+9a; x²+10x+21;

Вычислить рациональным способом: 0,836·3,76-1,164·1,26-0,836·1,26+1,164·3,76

Решить уравнение: 2x(2x-5)-(x-1)(5-2x) = 0.

Разность двух чисел равна 10. Если первое число увеличить на 3, а второе уменьшить на 2, то их произведение увеличится на 32. Найти эти числа.

Самостоятельная работа 6 (разность квадратов)

Вариант 1

1. Преобразовать многочлены к стандартному виду: (5a+b)(b–5a); (0,5xy²–3a)(0,5xy²+3a)+9a².

2. Разложить на множители: 4x²–9; 4x²y²–9a⁴; (x+2y)²-4x²; (a+2b)²-(2a-b)²; 16(x–y)²–25(x+y)²

3. Вычислите, используя формулы сокращенного умножения: 143²–142²; 197·203;

4. Упростите (a+1)(a²+1)(a⁴+1)(a–1)

5. Решить уравнение

Вариант 2

1. Преобразовать многочлены к стандартному виду: (5a+2b)(5a-2b);

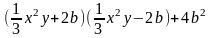
2. Разложить на множители: 9x²–4; 4x⁴y⁴–16a²; (2x-y)²-4x²; (a+3b)²-(a-b)²; 4(a–b)²–9(a+b)²

3. Вычислите, используя формулы сокращенного умножения: 234²–233²; 305·295; .

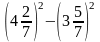4. Упростить: (1–b)(1+b²)(1+b⁴)(1+b)

5. Решить уравнение

Итог 2

Вариант 1

1. Упростить выражение и найти его значение при а=1, b=–2:

2. Решить уравнения: ; 7 – x = 4x–1

3. Записать в стандартном виде: а(а–2)+(а–4)²–(a–2)(2+а); (32х²–16х³у):(–8х²)–(9ху²–6х²у²):(3ху²)

4. Разложить на множители: (х–7)²–81; х³–3х²–4х+12; (a+1)(a–3) –2a(3–a)

5. В первом мешке в два раза больше муки, чем во втором. Когда из первого мешка взяли 30 кг муки, а во второй добавили 5 кг, то во втором стало муки в 1,5 раза больше, чем в первом. Сколько килограммов муки было в двух мешках первоначально?

6. Число а увеличили на 10%, а затем уменьшили на 50%. В результате получили число, которое на 90 меньше числа а. Найдите число а.

7. Найти НОД и НОК чисел а и b: а = 2⁹7³11; b = 2⁶7⁵3².

Вариант 2

1. Упростить выражение и найти его значение при z=2, y=–1:

2. Решить уравнения: ; x+2 = 2x–5

3. Упростить: 4х(х–5)+(х–3)²–(4–х)(4+х); (30х²–24х³у):(–6х²)–(8ху–12х²у²):(2ху)

4. Разложить на множители: (х–5)²–1; х³+2х²–9х–18; (a–1)(a–3)+(a+1)(3–a)

5. В первом мешке в 1,5 раза меньше картофеля, чем во втором. Когда в первый мешок добавили 20 кг картофеля, а из второго взяли 10 кг, то в первом мешке стало в два раза больше картофеля, чем во втором. Сколько картофеля было в каждом мешке первоначально?

6. Число b уменьшили на 15%, а затем увеличили на 40%. В результате получили число, которое на 57 больше числа b. Найдите число b.

7. Найти НОД и НОК чисел а и b: а = 2⁷3³5; b = 2⁶7⁵3⁴.

Самостоятельная работа 7 (алгебраические дроби)

1 вариант

Сократить дроби: ; ;

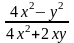Найти сумму (разность) алгебраических дробей: ; ; ; ; ; ;

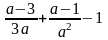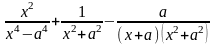
Решить уравнения: ; x²-4x+3=0

2 вариант

Сократить дроби: ; ;

Найти сумму (разность) алгебраических дробей: ; ; ; ; ; ;

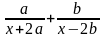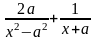Решить уравнения: ; x²-6x+8=0

Контрольная работа 3

1 вариант

Разложить на множители: 12x²-27; 8a³-12a²+6a-1; x²-4y²+3x+6y; m⁶-n⁶; 4b⁴–4b²+1–c²; 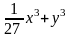; a²-9b²-a+3b; a³+a²-36

Решить уравнения: x²–9=0; x³+2x²+x+2=0

Сократить дробь

Вычислить рациональным способом 157²+15786+43²; 122217–29822+12281

2 вариант

Разложить на множители: 8x²-50; a³+9a²+27a+27; x²-4y²+5x-10y; m⁴-81; b⁴+2b²+1–4c²; 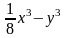; 4a²-b²-2a+b; a³+2a²-1

Решить уравнения: x²–49=0; x³-x²+2x-2=0

Сократить дробь

Вычислить рациональным способом 139²+139122+61²; 163217–362113+163145

Самостоятельная работа 8(3 вариант)

Построить графики

y=-2x при x<-1;

y=3x-2 при x≥1;

y= 1,5x-1

y=x-1-x

Найти точки пересечения графиков

y=2x-9 и y=5-2x;

y=x²-x+1 и y=1-2x

Найти k, если график функции y=kx+2 проходит через точку А(3;-1)

Найти линейную функцию, график которой параллелен графику функции y=-2x и проходит через точку В(1;2)

При каком значении аргумента функция y=2x²-1 принимает значение 7?

Контрольная работа 4 (3 вариант)

1. Найдите уравнение прямой, проходящей через точки А(3;1) и В(–2; 4).

2. Найдите точки пересечения графиков функций y=5x–6 и y=21–2x.

3. Постройте график функции y=x-5-3

4. Точка В лежит на луче АС за пределами отрезка АС. Постройте график зависимости длины y отрезка АВ от длины x отрезка ВС, если длина отрезка АС равна 4.

5. Найдите точки графика функции y=2x, произведение координат которых равна 18

6. Проведите исследование функции по заданному графику.

7. При каких значениях а графики функций y= a²x+3 и 4x-1 параллельны?

8. В 7¹ и в 7⁵ классе всего 12 человек зовут Саша. Если 40% Саш перевести из 7¹ в 7⁵, а затем седьмую часть Саш, оказавшихся в 7⁵, перевести обратно в 7¹, то в этих классах окажется поровну Саш. Сколько всего Саш в 7¹ и в 7⁵ классах по отдельности?

Системы (3 вариант)

1. Построить графики функций y=x+1-2;

2. Решить системы уравнений ; ; ;

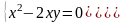Системы 2 (3 вариант)

Контрольная работа 5