Самостоятельная работа 1

1 вариант

1. Найдите значение числового выражения:

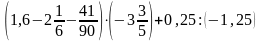
2. Упростите алгебраическое выражение 2(0,3x–1,05y)–0,4(4x–0,25y) и вычислите его значение при x=3,3 и y=–2,9

3. Раскрыть модуль 2x–3–3(x+2–1)

4. Записать решение задачи формулой: Из города со скоростью 60км/час выехал автомобиль. Через час за ним со скоростью 50км/час выехал другой автомобиль. Какое расстояние будет между автомобилями через t часов после выезда первого автомобиля?

5. Число a дает при делении на 7 остаток 2, а число b – остаток 3. Какой остаток дает при делении на 7 число a + 2b?

6. Какое количество воды надо добавить к 10 литрам 40%-го раствора кислоты, чтобы получить 20%-й раствор.

2 Вариант

1. Найдите значение числового выражения:

2. Упростите алгебраическое выражение 0,2(1,3x–0,45y)–0,04(4x+0,25y) и вычислите его значение при x=3,1 и y=–1,9

3. Раскрыть модуль 3x+5–2(x–1+3)

4. Записать решение задачи формулой: Из города А со скоростью v км/час выехал автомобиль. Через час навстречу ему из города B со скоростью 50км/час выехал другой автомобиль. Через какое время после выезда первого автомобиля они встретятся, если расстояние между городами S километров?

5. Число a дает при делении на 11 остаток 3, а число b – остаток 6. Какой остаток дает при делении на 7 число 2a + b

6. Какое количество воды надо добавить к 10 литрам 50%-го раствора кислоты, чтобы получить 10%-й раствор

Самостоятельная работа 2

Вариант 1

Решить уравнения: 4x – 2(x+1) = 5 – 3(x-2); 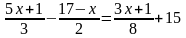; (2x–3)(x+8) = 0; ; ;

Вариант 2

Решить уравнения: 5x –3(x–1) = 4 – 2(x+3); 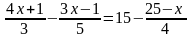; (2x+8)(x–6) = 0; ; ;

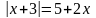Контрольная работа 1

Вариант 1

1. Найти числовое значение выражения: 1,472,02 – 2,250,67 + 0,231,47

2. Для данных алгебраических выражений 8x – 0,5y и 3x + 2y найти их сумму, разность между первым и вторым, разность между удвоенным вторым и утроенным первым.

3. Решить уравнение

4. Решить уравнение: 8 – x = 4x.

5. При каких значениях параметра а уравнение (a+1)(a–2)x = a²+2a не имеет решений?

6. У Васи на 40% больше двоек, чем у Вовы, а у Гриши на 10% больше двоек, чем у Васи. На сколько процентов больше двоек у Гриши, чем у Вовы?

7. Доказать, что сумма трех идущих подряд чисел делится на 3.

8. Ваня и Даня каждый день бегают по кругу в течение одного и того же времени. Когда они бегут в одну сторону, то Ваня обгоняет Даню три раза, когда они бегут в разные стороны, то Даня встречает Ваню 9 раз. Во сколько раз скорость Вани больше?

9. Сколько решений имеет уравнение 4x+3y =48, если известно, что x и y – натуральные числа?

Вариант 2

1. Найти числовое значение выражения: 2,431,04 – 1,50,83 + 0,462,43

2. Для данных алгебраических выражений 4x + 1,5y и 5x – 4y найти их сумму, разность между вторым и первым, разность между удвоенным первым и утроенным вторым.

3. Решить уравнение

4. Решить уравнение: 5 – 2x = 7x.

5. При каких значениях параметра а уравнение (a+3)(a–1)x = a²–a не имеет решений?

6. У Кати на 30% апельсинов больше, чем у Тани, а у Маши на 20% апельсинов больше, чем у Кати. На сколько процентов у Маши апельсинов больше, чем у Тани?

7. Доказать, что сумма пяти идущих подряд чисел делится на 5.

8. Маша и Саша каждый день бегают по кругу в течение одного и того же времени. Когда они бегут в одну сторону, то Саша обгоняет Машу 4 раза, когда они бегут в разные стороны, то Маша встречает Сашу 8 раз. Во сколько раз скорость Саши больше?

9. Сколько решений имеет уравнение 4x+5y =80, если известно, что x и y – целые неотрицательные числа?

Самостоятельная работа 3

Вариант 1

1. Сколькими способами x¹² можно записать в виде степени?

2. Записать в виде степени: (a+b)⁴(a+b)³; (x–y)⁶(y–x)⁵; 8x⁶

3. Вычислить: ; 8¹²2⁴:4¹⁸; 12⁵3:6⁶

4. Записать число в стандартном виде: 271,34; 12000000

5. Упростить выражение: ; (2x)⁴(2x⁴)

6. Найти НОД и НОК чисел а и b: а = 2¹⁰7³13; b = 2⁶7⁵3⁴.

7. Петя доказал теорему: при умножении двух чисел, записанных в стандартном виде, порядок произведения равен сумме порядков. Прав ли Петя?

Вариант 2