5.6. Напірна радіальна фільтрація газу в пласті

Прикладом радіальної фільтрації є приплив газу до свердло­вини, що пробурена на всю товщину пласта, коли нижній кінець обсадної колони зупиняється в покрівлі пласта.

Будемо вважати, що на віддалі Rk знаходиться так званий контур живлення. Розрахункова схема фільтрації зображена на рис.5.3.

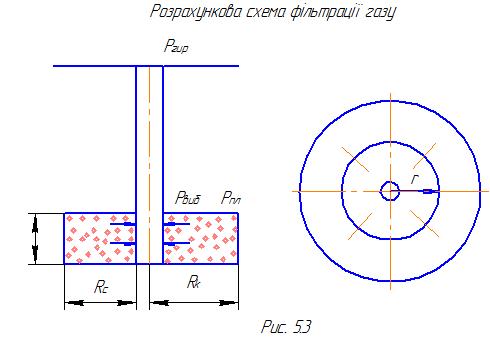
Введемо такі позначення:

Pпл - пластовий тиск на контурі живлення свердловини;

Рвиб- тиск не вибої свердловини Сна стінці свердловини);

Rс - радіус свердловини;

Т - абсолютна температура газу в пласті;

Z - коефіцієнт стисливості газу в умовах пласта;

R -газова постійна;

η - динамічна в"язкість газу;

M - масова витрата газу в пласті;

Вважаємо, що режим фільтрації лінійний, фільтрація стаціонар­на, процес фільтрації ізотермічний, Свердловина гідравлічно досконала, пласт однорідний.

Вихідні рівняння мають вигляд: флрмула Дарсі для швидкості фільтрації в напрямі радіуса

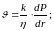(5.16)

рівняння стану реального газу

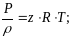(5.17)

рівняння нерозривності потоку газу

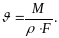(5.18)

В формулі (5.18) F - це бокова поверхня циліндра довільного радіуса r , через яку протікає рідина

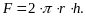(5.19)

Розв'язуємо сумісно рівняння (5.15) - (5.18) з врахуванням (5.19)

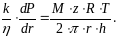(5.20)

Розділивши змінні і проінтегрувавши, одержимо

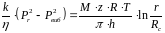(5.21)

При 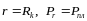, тому

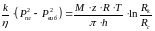(5.22)

Розв'язуєм сумісно рівняння (5.21) і (5.22) відносно тиску в довільній точці пласта

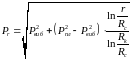(5.23)

Як бачимо, тиск в довільній точці є логарифмічна функція від­далі від цієї точки до осі свердловини. Для всіх точок, в яких

r=const , тиск буде однаковий. Це рівняння ізобар, щоявляють собою концентричні відносно осі свердловини кола.

Рівняння (5.22) розв'язуємо відносно масової витрати газу в пласті

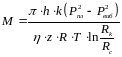(5.24)

Ця формула носить ім"я Дюпюї по прізвищу її автора.

Однак витрати газу в підземному зберіганні газу прийнято вимірювати не в масових, а в об’ємних одиницях, приведених до стандартних умов.

Використовуючи рівняння нерозривності потоку і рівняння стану для" стандартних умов ( То = 293К, Ро = 760 мм рт.ст. =1013 МПа)

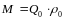(5.25)

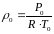(5.26)

одержуємо розрахункову формулу для визначення продуктивності (дебіту) газової експлуатаційної досконалої свердловини

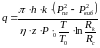(5.27)

Аналогічну формулу можна одержати для нагнітальної свердловини. Враховуючи вигляд формули Дарсі в цьому випадку

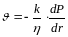(5.28)

одержуємо

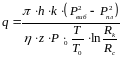(5.29)

7. Поняття про інтерференцію і гідродинамічну досконалість свердловин

Підземне сховище газу має десятки свердловин. Для практики проблема взаємодії свердловин, тобто задача про залежність дебі­ту сховища від кількості свердловин, є дуже важлива.

Якщо свердловини знаходяться на великих віддалях, то вони практично не впливають одна на іншу. Сумарний дебіт групи сверд­ловин дорівнює сумі дебітів при їх окремій роботі. Розподіл пластових тисків в цьому випадку має вигляд, зображений на рис. 5.4.

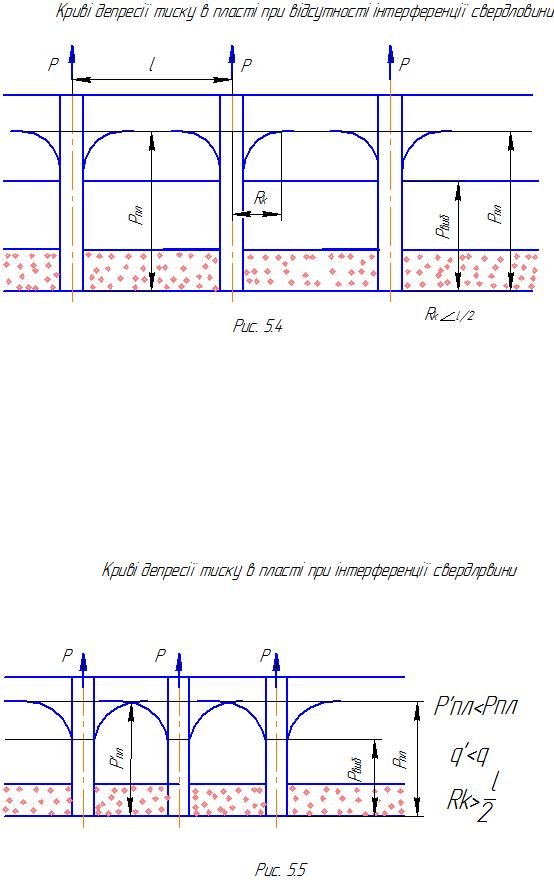
При введенні в експлуатацію нових свердловин обов"язково наступає момент, коли починається взаємний вплив свердловин. Сумарний дебіт групи свердловин стає меншим суми дебітів при їх незалежній роботі. Це явище називають інтерференцією свердловин. Розподіл пластових тисків в цьому випадку має вигляд, зображений на рис. 5.5.

Звичайно графік залежності сумарного відбору газу із пласта від •іисла свердловин має вигляд кривої, показаної на рис.5.6.

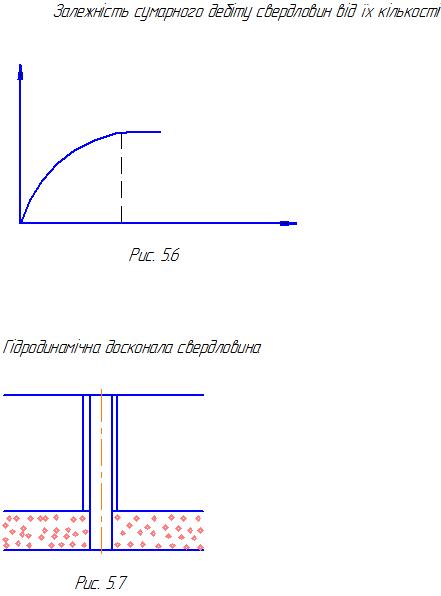
Із рис.5.6 слідує, що інтерференція свердловин деформує поле пластових тисків, веде до їх зниження і тим самим зменшує дебіт свердловин.

Гідравлічно досконала свердловина розкриває пласт на всю товщину і має відкритий вйбій, тобто стовбур свердловини в межах продуктивного пласта не обсаджений колоною труб (див.рис.5.7).

Такі свердловини можна експлуатувати тільки г^ри великій міцності привибійної зони пласта і відсутності¹ підошовної води.