2. Результаты моделирования в среде MahtLab

В главе Error: Reference source not found показано, что горизонтальные предельные прогибы опор конвейерных галерей от ветровых нагрузок, ограничиваемые исходя из технологических требований, следует принимать равными h/250 (где h - высота опор от верха фундамента до низа ферм или балок), горизонтальные предельные прогибы колонн (стоек) каркасных зданий от температурных климатических и усадочных воздействий следует принимать равными h_s/150 ÷ h_s/120 в зависимости от материалов (h_s – высота этажа, а для одноэтажных зданий с мостовыми кранами - высота от верха фундамента до низа балок кранового пути).

Для моделирования согласно изложенным выше требованиям к строительным сооружениям было принято за основу расчетов, что максимально-типичными размерами для промышленных сооружений будем считать, что высота составляет 25 метров, длина порядка 100 метров. Для модели были взяты следующие значения параметров: расстояние до первого РМ (z₀) варьировалось от 10 до 15 метров; длина зоны контроля (L) от 50 до 100 метров, смещения в горизонтальной и вертикальной плоскости от 5 до 25 метров.

Погрешность измерений смещений 0,1-0,2 мм в диапазоне 5 мм для элементов конструкции перекрытий, а для элементов конструкции колонны отклонения составляют максимум 15 мм, погрешность таких измерений не более 0,7 мм.

Исходя из поставленных условий была смоделирована ситуация для определения типичных параметров ИК РОЭС.

На рисунках 1 .8 – 1 .11 представлены результаты моделирования в среде MathLAB для вариант вертикального смещения фотоприемного модуля.

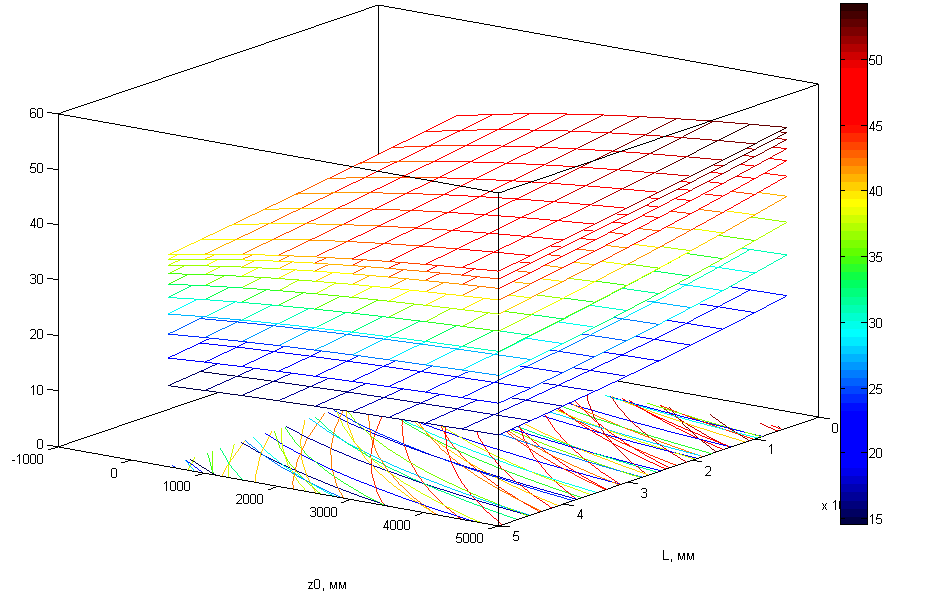Рисунок

y=7м.

1.8 – Зависимость углового поля зрения объектива фотоприемного модуля 2 от расстояния до первой КМ (z₀), длины зоны контроля (L) и изменения высоты плоскости расположения зоны КМ (y).

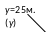
y=7м.

y=5м.

Рисунок

1.9 – Минимальное угловое расстояние между РМ в зависимости от расстояния до первой РМ (z₀), длины зоны контроля (L) и изменения высоты плоскости расположения зоны РМ (y).

y=5м.

y=7м.

y=25м.

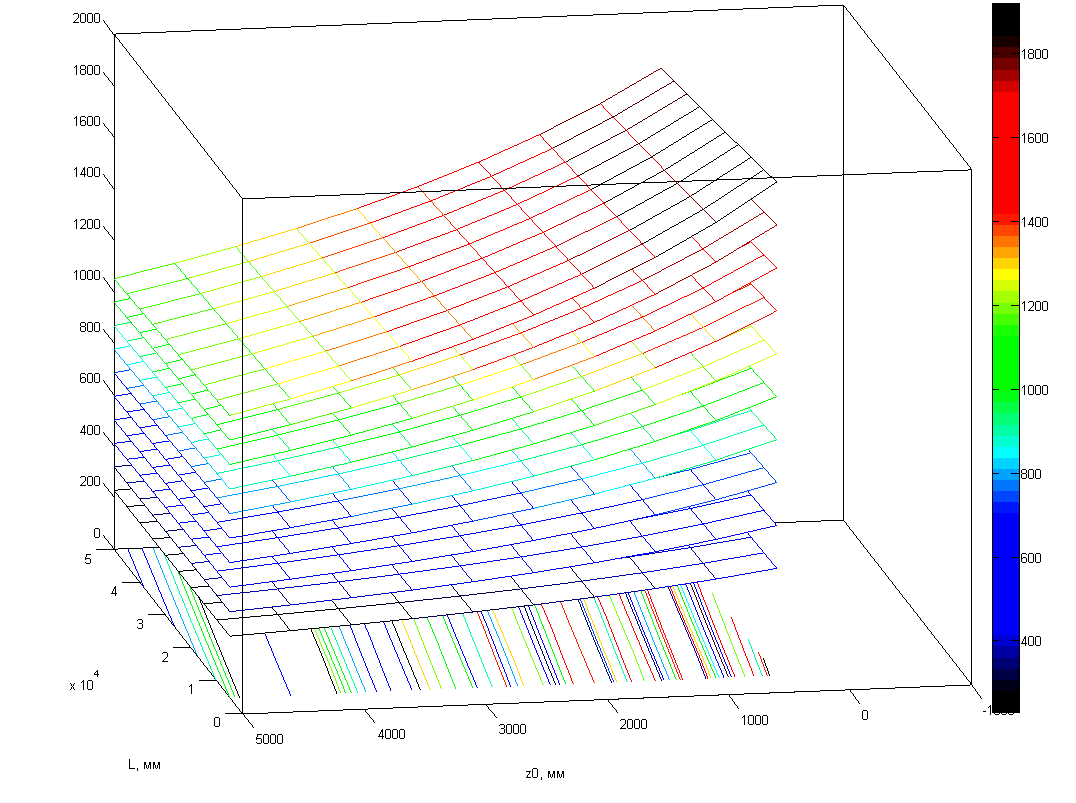Рисунок

1.10 – Минимальное линейное перемещение РМ от расстояния до первой РМ (z₀), длины зоны контроля (L) и изменения высоты плоскости расположения зоны РМ (y).

y=25м.

y=7м.

y=5м.

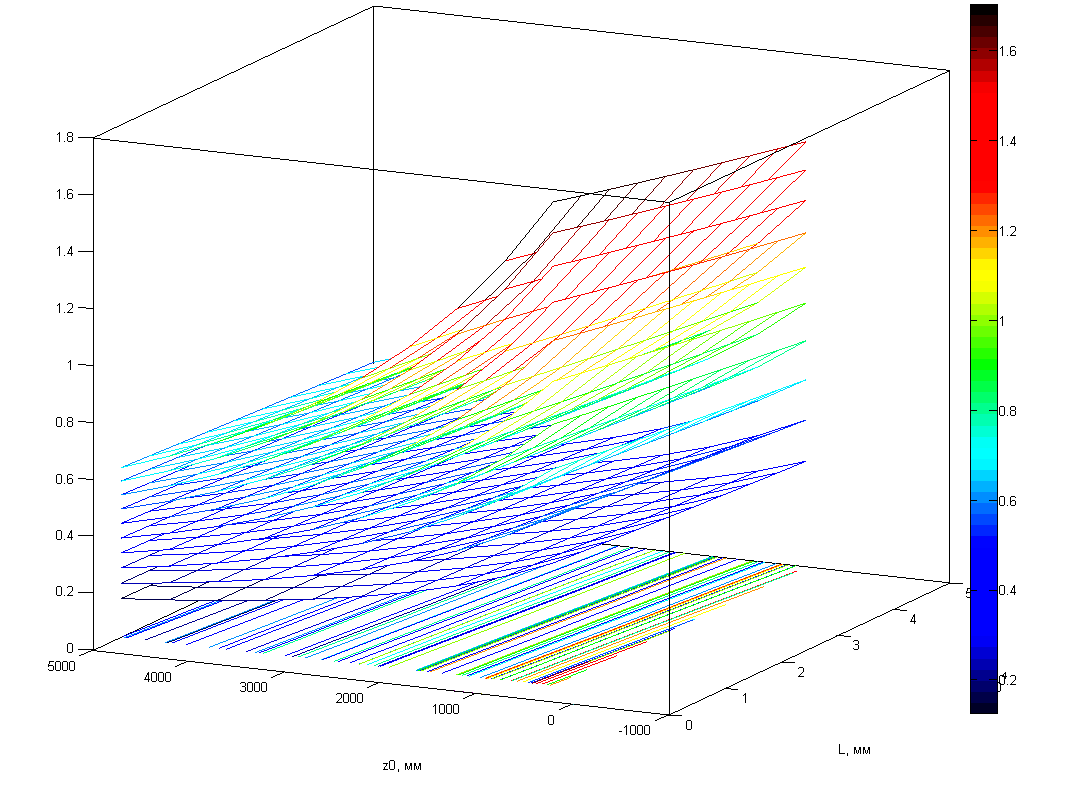Рисунок

1.11 – Минимальное угловое перемещение РМ метки в зависимости от расстояния до первой РМ (z₀), длины зоны контроля (L) и изменения высоты плоскости расположения зоны РМ (y).

На рисунках 1 .12 – 1 .15 представлены результаты моделирования в среде MathLABдля вариант горизонтального смещения фотоприемного модуля.

y=5м.

y=7м.

y=25м.

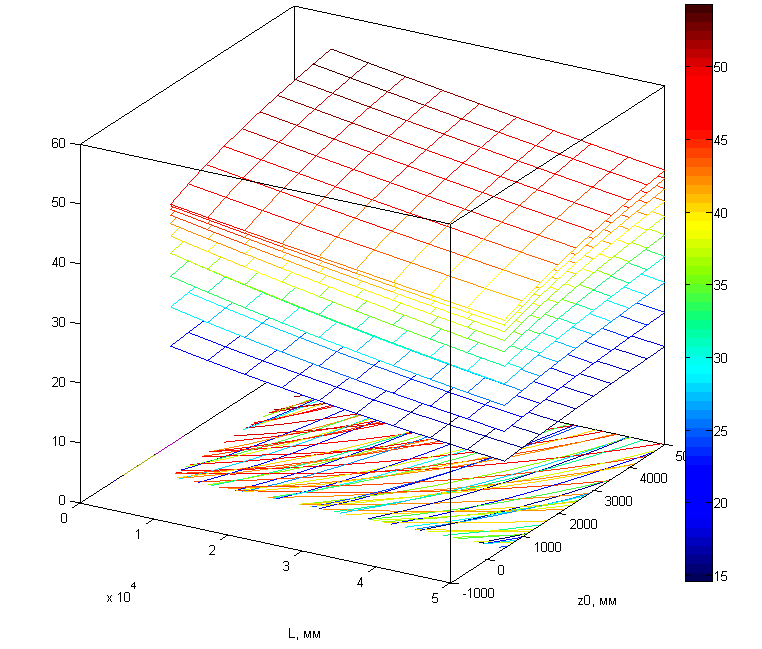Рисунок

1.12 – Зависимость углового поля зрения объектива фотоприемного модуля от расстояния до первой РМ (z₀), длины зоны контроля (L) и горизонтального смещения фотоприемного модуля (y).

y=5м.

y=7м.

y=25м.

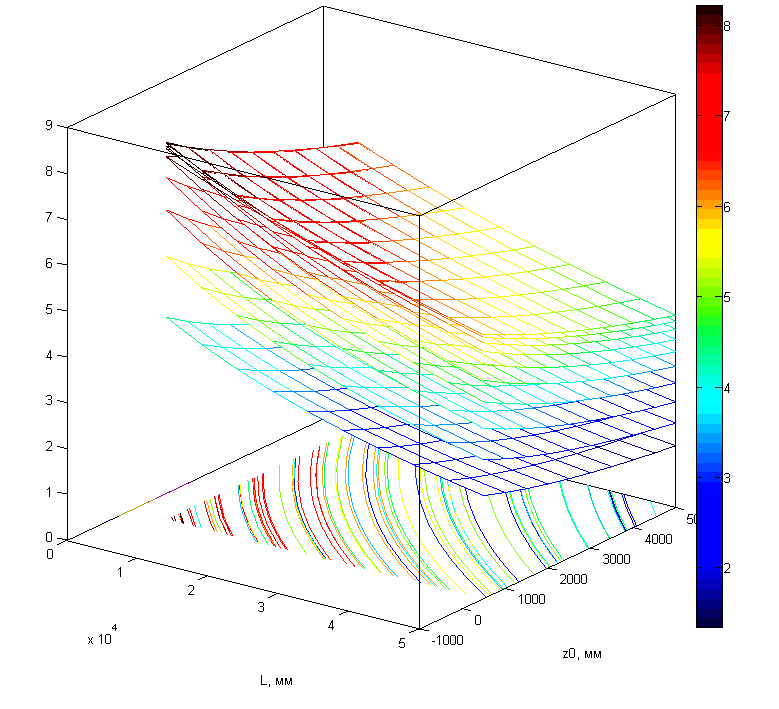Рисунок

1.13 – Минимальное угловое расстояние между РМ в зависимости от расстояния до первой РМ (z₀), длины зоны контроля (L) и изменения высоты плоскости расположения зоны РМ (y).

y=25м.

y=7м.

y=5м.

Рисунок

1.14 – Минимальное линейное перемещение РМ от расстояния до первой РМ (z₀), длины зоны контроля (L) и изменения высоты плоскости расположения зоны РМ (y).

y=5м.

y=7м.

y=25м.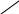

Рисунок

1.15 – Минимальное угловое перемещение РМ от расстояния до первой РМ (z₀), длины зоны контроля (L) и изменения высоты плоскости расположения зоны РМ (y)

На рисунках 1 .16 – 1 .19 представлены результаты моделирования в среде MathLAB для вариант двухкоординатного смещения фотоприемного модуля (по вертикали и горизонтали).

y=25м.

y=7м.

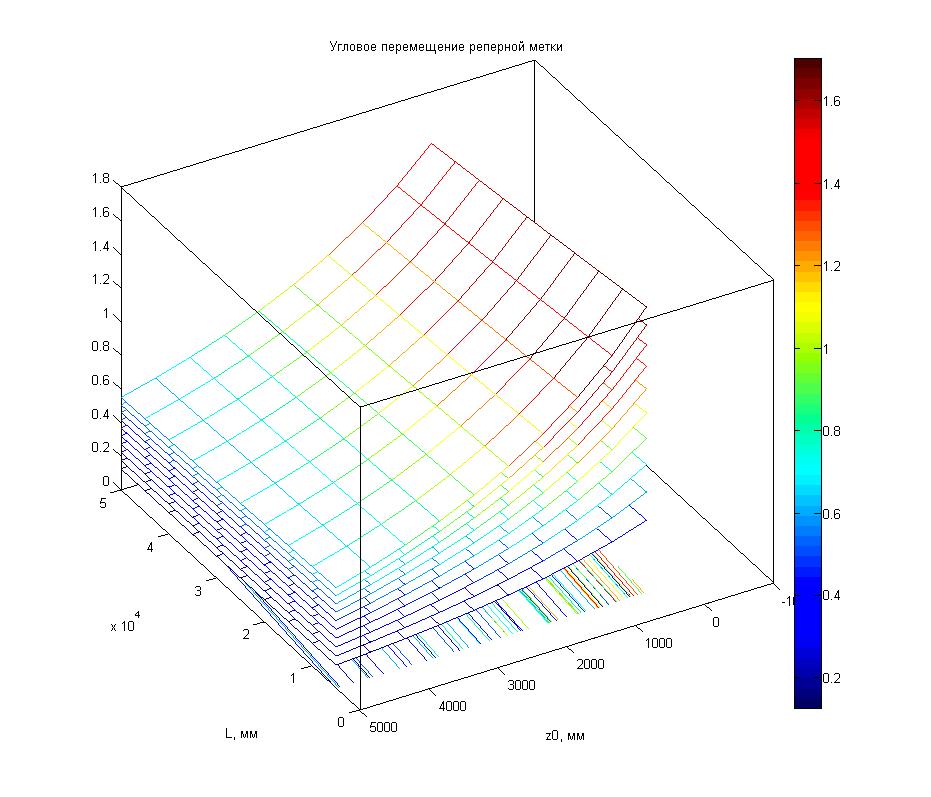
y=5м.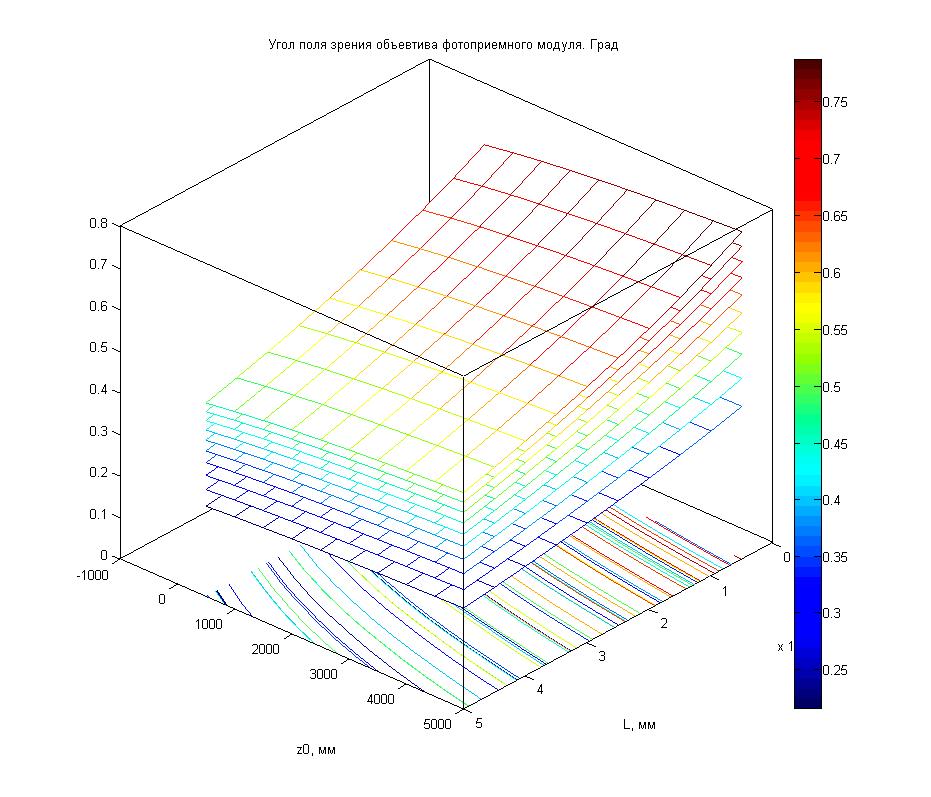

Рисунок

1.16 – Зависимость углового поля зрения объектива фотоприемного модуля от расстояния до первой РМ (z₀), длины зоны контроля (L) и горизонтального смещения фотоприемного модуля (y).

y=5м.

y=25м.

y=7м.

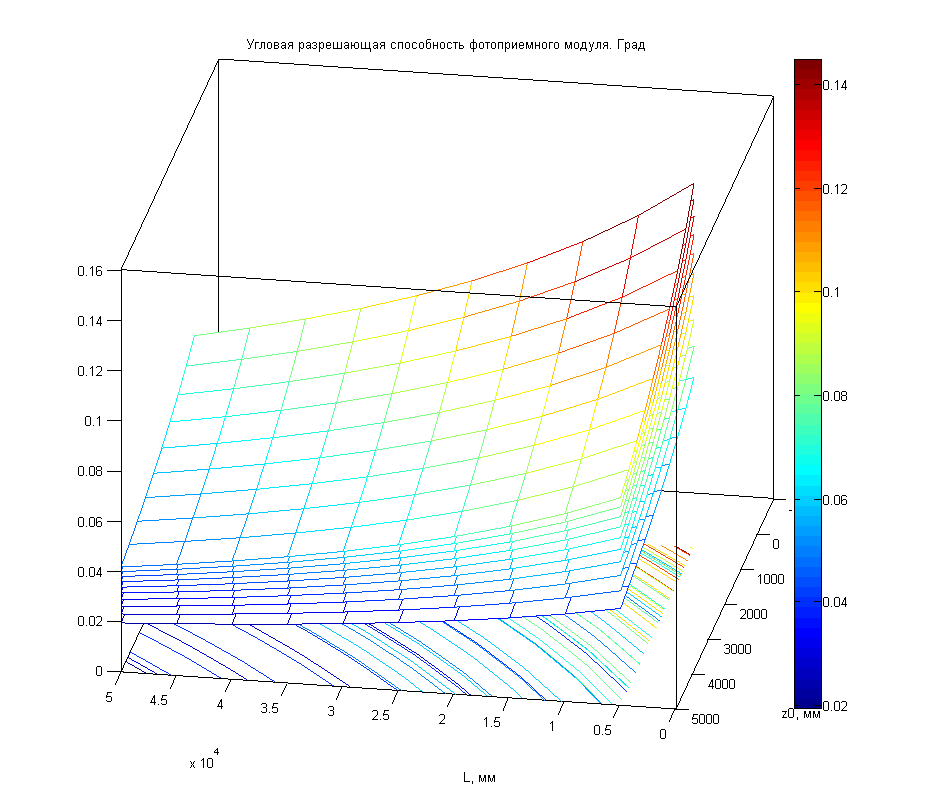Рисунок

1.17 – Минимальное угловое расстояние между РМ в зависимости от расстояния до первой РМ (z₀), длины зоны контроля (L) и изменения высоты плоскости расположения зоны РМ (y).

y=5м.

y=7м.

y=25м.

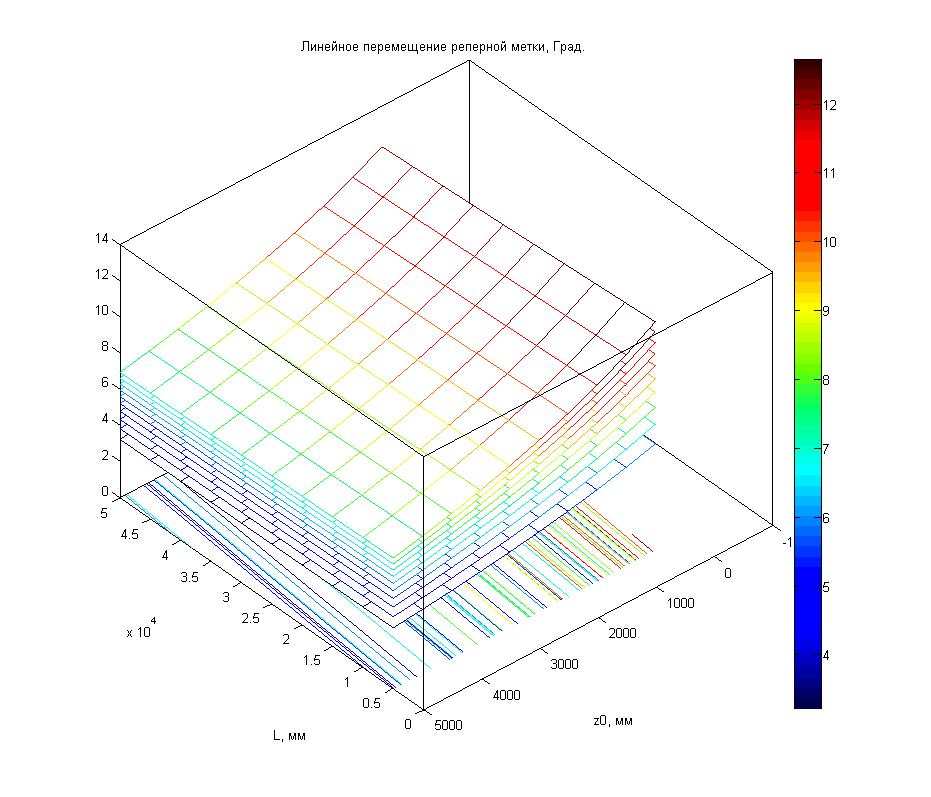Рисунок

1.18 – Минимальное линейное перемещение РМ от расстояния до первой РМ (z₀), длины зоны контроля (L) и изменения высоты плоскости расположения зоны РМ (y).

y=5м.

y=7м.

y=25м.

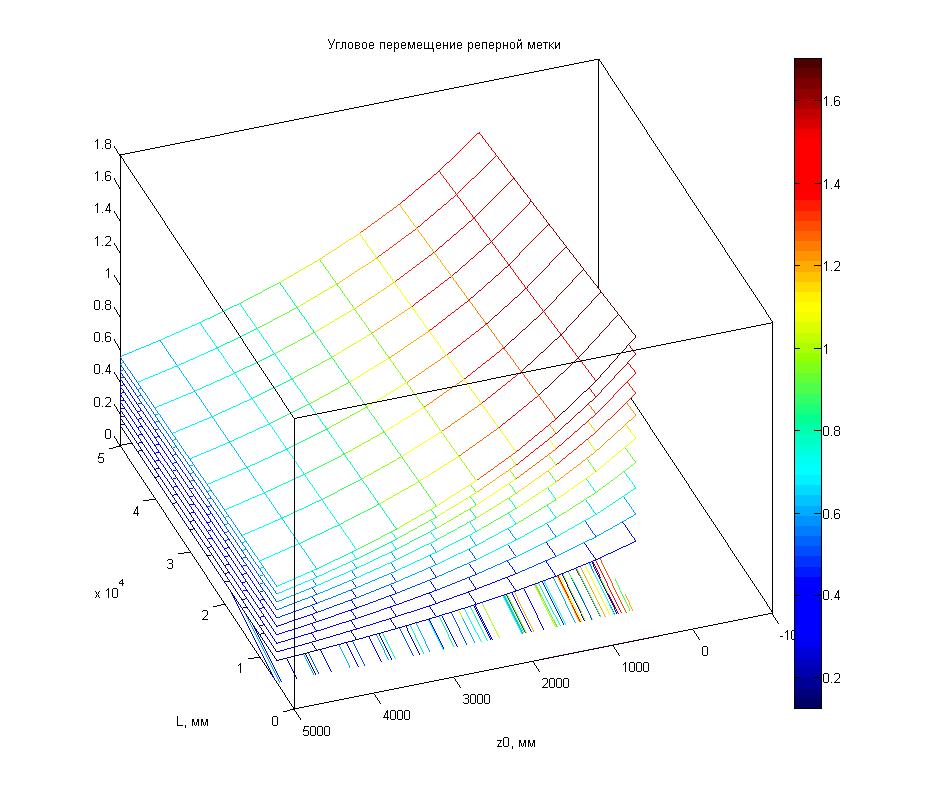Рисунок

1.19 – Минимальное угловое перемещение РМ от расстояния до первой РМ (z₀), длины зоны контроля (L) и изменения высоты плоскости расположения зоны РМ (y)

1. Выводы

На основании анализа технических требований к пространственному положению элементов при эксплуатации сооружений обосновано, что предельные значения контроля РОЭСПТК смещений:

- элементов конструкции перекрытий не должно превышать 5 мм при погрешности не более 0,1 - 0,2 мм.

- элементов конструкции колонн предельные отклонения относительно монтажных осей не должны 15 мм при отклонении осей колонн от вертикали в верхнем сечении (при высоте колонн до 15 м), при погрешности не более 0,5 – 0,7 мм.

Получено выражение для вычисления линейных величин разрешающей способности матричного поля анализа при различных величинах перемещения реперной контрольной метки в случае, когда плоскость установки матричное поле ортогональна биссектрисе угла поля зрения объектива совпадающей с оптической осью этого объектива.

Разработаны программы и алгоритмы для расчета параметров РОЭСПТК при контроле элементов конструкций и сооружений при различных смешениях базового блока в вертикальной плоскости системы координат строительных или монтажных осей.

Проведен теоретический анализ влияния основных параметров схемы блоков РОЭСПТК на параметры элементарного фотоприемного модуля, реализованного в виде единого матричного поля; из графиков представленных на рисунках 1 .8 – 1 .19 видно, что зависимость носит слабую нелинейную зависимость и можно считать линейной.

Результаты математического моделирования в среде MahtLAB показали, что оптимальным с точки зрения минимальных смещений элементов РОЭСПТК является смещение базового блока в плоскости соединяющей контрольные метки.