Задача 6

Определите число реакторов идеального смешения (каждый объемом 1 м³), установленных каскадом, чтобы при постоянной скорости подачи реакционной смеси 0,8 м³/с для осуществления реакции первого порядка с константой скорости 1 с⁻¹ получить на выходе из последнего реактора концентрацию исходного вещества менее 5 % от начальной.

Решение

Уравнение зависимости концентрации вещества А от времени при протекании в реакторе идеального смешения реакции первого порядка с константой скорости k при заданной скорости подачи реакционной смеси v и объеме реактора V имеет вид

.

Стационарное состояние достигается быстро, и тогда можно рассчитать

.

Концентрация на выходе из первого реактора каскада соответствует начальной концентрации для второго реактора в каскаде и т. д. Краткий ответ: нужно четыре реактора.

Задача 7 Превращение роданистого аммония в тиомочевину − обратимая мономолекулярная реакция

.

За изменением количества прореагировавшего роданида аммония стали наблюдать спустя некоторое время после начала реакции, причем отсчет времени начали с момента определения количества роданида в первый раз:

Время определения, мин	0	19	38	48	60
Количество прореагировавшего роданида аммония, %	2,0	6,9	10,4	12,3	13,6

При достижении состояния равновесия 21,2% роданистого аммония превратилось в тиомочевину.

Найти константу скорости прямой и обратной реакции, а также время от начала реакции до начала наблюдения.

Решение

Запишем приведенную в условии задачу в символьном варианте

Общий вид кинетической кривой обратимой реакции приведен на рис. 2.2.

Рис. 2.2

Запишем балансовые соотношения для исходного вещества и для продукта реакции

; .

Обратимой реакции первого порядка соответствует интегральное кинетическое уравнение

.

Известно, что = 21,2% .

Приведем данные таблицы к виду, удобному для подстановки в интегральное кинетическое уравнение

Время определения, мин	0	19	38	48	60
	2,0	6,9	10,4	12,3	13,6

Строим графическую зависимость от времени (рис.2.3):

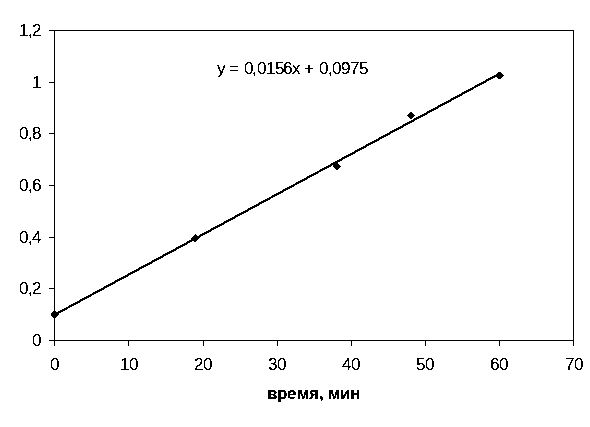
Рис.2.3

Угловой коэффициент прямой равен = 0,0156 мин⁻¹ .

Константа равновесия связана с константами скоростей прямой и обратной реакций

.

Решая систему

= 0,0156 мин⁻¹; ,

можно найти константы скоростей по отдельности.

Задача 8

Для обратимой реакции первого порядка константа равновесия равна 8, а константа скорости прямой реакции 0,4 с⁻¹ . Начальная концентрация вещества В равна 0. Вычислите время, при котором концентрации веществ А и В станут равными.

Решение

Известно соотношение между константой равновесия обратимой реакции и константами скоростей прямой и обратной стадий:

.

Отсюда находим .

Интегральное уравнение скорости обратимой реакции первого порядка имеет вид:

.

Величину предельной плотности глубины реакции можно найти как:

.

По условию задачи нужно выразить время, при котором концентрации веществ А и В станут равными, т.е. x = .

Задача 9

Константа скорости прямой и обратной реакций равны, соответственно, 15 с⁻¹ и 1 с⁻¹ . Вычислить текущие концентрации вещества А и В через 0,08 с после начала реакции, если начальные концентрации А и В равны 0,02 моль/л.

Решение

Текущие концентрации вещества А и В могут быть найдены по балансовым соотношениям:

; .

Интегральное кинетическое уравнение обратимой реакции имеет вид

,

где величина равновесной плотности глубины реакции находится как

.

Используя все эти уравнения и данные условия задачи, находим плотность глубины реакции, наблюдаемую через 0,08 с после начала реакции x , а затем и текущие концентрации участников реакции.

Задача 10

Кинетика обратимой реакции первого порядка исследована при двух температурах. Получены следующие данные:

При 293 К

Время, мин	0	15	
Содержание В в смеси в %	2	43,3	57,8

При 313 К

Время, мин	0	9	
Содержание В в смеси в %	2	55,6	62,8

Найдите энергии активации прямой и обратной реакций.

Решение

По таблице, данной в условии задачи, при 293 К равновесная плотность глубины реакции =0,587 , а равновесные концентрации веществ равны = 0,578 , а = (1−0,578) .

Исходя из этих данных, решаем систему уравнений:

;

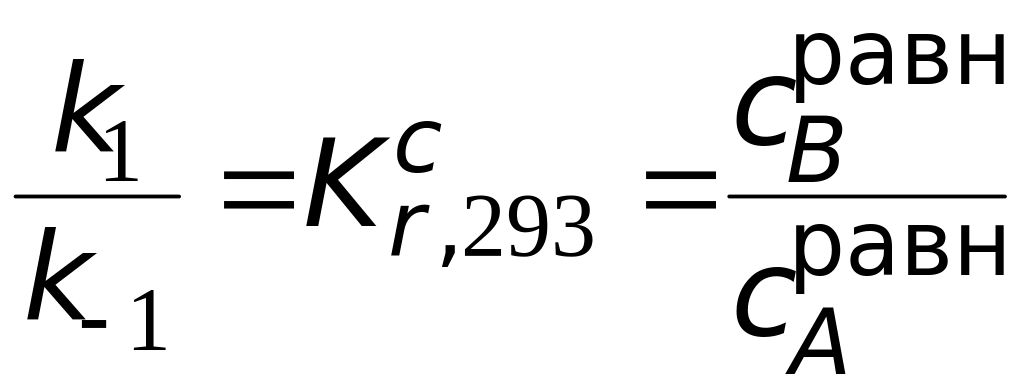
И находим константы скорости прямой и обратной реакций при 293 К. Затем ту же процедуру проводим с данными о реакции при 313 К. По таблице при 313 К 0,628 , = 0,628 , а = (1−0,628) . Затем, располагая данными о значениях констант скоростей прямой и обратной стадий при двух температурах, нетрудно найти и величины энергий активации.