Задача 3
Константа скорости разложения органической кислоты зависит от температуры следующим образом:
Т, К k · 102 , с 1
275 5,45
287 10,54
293 12,78
303 22,20
Определить графически параметры уравнения Аррениуса.
Решение
Уравнение Аррениуса имеет вид
,
где
k
− константа
скорости реакции;
предэкспоненциальный множитель;
эмпирически найденная энергия активации.
Представив это уравнение в логарифмическом виде, получим
, или
.
(1.2)
Последнее
выражение особенно удобно для графического
построения. Линейная зависимость
получается, если экспериментальные
данные представить в координатах ln
k
−
.
Как следует из анализа уравнения (1.2),
угловой коэффициент прямой в этих
координатах будет равен
.
Переводим данные условия задачи к виду, необходимому для построения графической зависимости (табл. 1.2).
Таблица 1.2
Величина |
Значения |
|||
k ·102 , с 1 |
5,45 |
10,54 |
12,78 |
22,20 |
Т, К |
275 |
287 |
293 |
303 |
ln k |
−2,91 |
−2,25 |
−2,06 |
−1,51 |
103/Т, К−1 |
3,64 |
3,48 |
3,41 |
3,30 |
Строим графическую зависимость ln k − (рис.1.7), определяем угловой коэффициент прямой и находим величину энергии активации.
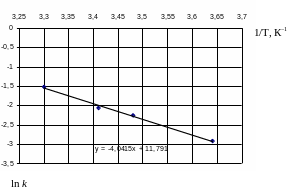
Рис. 1.7
При компьютерном построении рисунков возможно проводить линеаризацию экспериментальных данных, используя линию тренда соответствующей формы − в данном случае линейной. Тогда из уравнения линии тренда, которое появляется на плоскости рисунка, сразу виден угловой коэффициент прямой. Для нашей задачи он равен −4,0415. Отсюда энергия активации равна 33 601 Дж/моль.
Величина
предэкспоненциального множителя
довольно легко определяется из уравнения
линии тренда:
= 11,791.
Следовательно, = 1,32∙105 с−1.
Задача 4
Какая доля новокаина (%) разложится за 10 суток его хранения при 293 К, если константа скорости гидролиза новокаина при 313 К равна 1 105 сут1, а энергия активации реакции 55,2 кДж/моль.
Решение
Уравнение Аррениуса в дифференциальной форме
.
Берем определенный интеграл
,
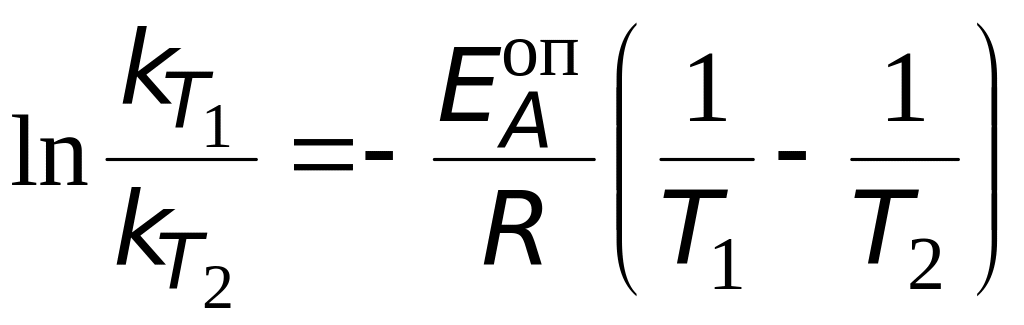или
.
Отсюда находим неизвестную константу скорости:
.
Предполагая, что новокаин разлагается по реакции первого порядка, воспользуемся интегральным уравнением реакции первого порядка:
.
Нас
интересует, какая доля разложится, т.
е. 1 −
.
Задача 5
Вычислите значение энергии активации, при которой температурный коэффициент скорости некоторой реакции в интервале температур от 27 оС до 37 оС равен 2,5. На сколько градусов нужно повысить температуру реакции, чтобы ее скорость увеличилась в 100 раз?
Решение
Температурный коэффициент скорости реакции
= 2,5.
.
Энергия активации равна 70 848 Дж/моль.
Воспользуемся уравнением Аррениуса в интегральной форме:
.
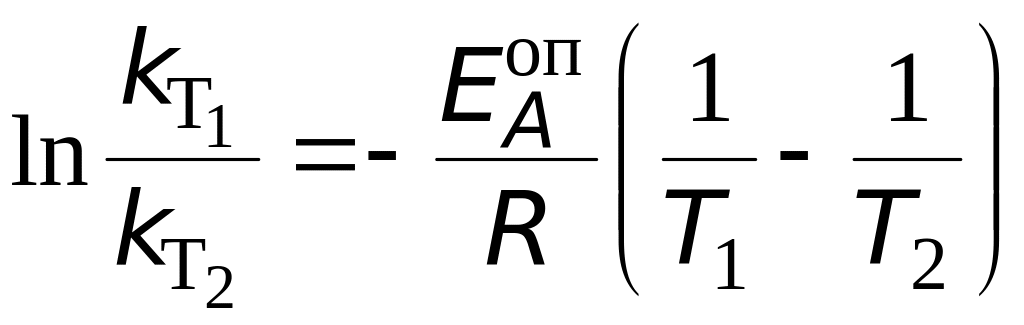Считая, что все остальные условия в двух сравниваемых опытах одинаковы (концентрация, давление, растворитель и т. д.), находим
.
.
Далее
следует определить
.