1.2.3. Последовательные реакции

Последовательные реакции − это такие реакции, которые состоят из последовательных элементарных стадий. Промежуточные вещества, которые образуются в одной стадии, расходуются в последующей.

Обычно очень трудно рассчитать концентрацию промежуточного вещества в любое время. Аналитические выражения получены только для последовательных реакций с двумя односторонними мономолекулярными элементарными стадиями.

Последовательную реакцию можно изобразить схематично как

или в виде системы стадий:

, закон скорости ;

, закон скорости .

где  скорости и константы скоростей первой и второй стадий реакции соответственно;  концентрации исходного вещества и промежуточного вещества соответственно. Чтобы найти в явном виде зависимость от времени, нужно проинтегрировать дифференциальное кинетическое уравнение для первой стадии.

Дифференциальное кинетическое уравнение первой стадии

.

Интегральное кинетическое уравнение первой стадии

.

Уравнение кинетической кривой для исходного вещества

.

Суммарная скорость образования промежуточного вещества равна алгебраической сумме скоростей образования вещества P в первой стадии и расходования его во второй стадии. Запишем ее с учетом знаков:

.

.

Для того чтобы решить дифференциальное уравнение, преобразуем его следующим образом: сгруппируем переменные и умножим обе части уравнения на величину . При этом нужно учесть, что в левой части

.

Теперь получим

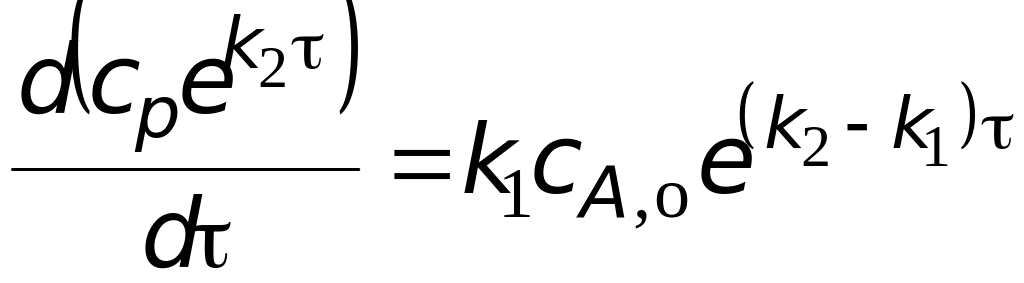. (1.7)

Интегрирование уравнения (1.7) от 0 до и от 0 до приводит к выражению

. (1.8)

Теперь из уравнения (1.8) легко выразить в явном виде зависимость концентрации промежуточного вещества от времени:

.

Уравнение кинетической кривой для продукта последовательной реакции можно получить как интегрированием соответствующего дифференциального уравнения, так и по уравнению материального баланса, так как выражения кинетической кривой для исходного вещества и для промежуточного продукта мы только что вывели. Этот способ проще, им и воспользуемся.

В любой момент времени .

Следовательно, легко получить

.

Общий вид кинетических кривых представлен на рис. 1.5, где 1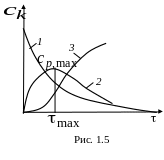 – зависимость концентрации исходного вещества от времени; 2 – то же промежуточного вещества от времени; 3 – то же продукта реакции от времени.

Как видно из рис. 1.5, на кинетической кривой промежуточного вещества 2 имеется максимум, а на кинетической кривой продукта – некоторый период с очень малой скоростью реакции, так называемый индукционный период. В этот период идет в системе накопление промежуточного продукта (его еще мало) и конечного продукта в системе почти нет.

Легко видеть из расположения кривых, что максимум на кривой промежуточного продукта совпадает по времени с точкой перегиба на кривой конечного продукта. Кинетическая кривая такого вида, какой имеет кинетическая кривая конечного продукта 3, называется s-образной кривой. Часто такие кривые наблюдаются при автокаталитических реакциях.

Конечно, если мы говорим о максимумах и о точках перегиба, то, имея уравнения линий, мы легко найдем координаты максимума и точки перегиба. Например, найдем координаты максимума на кинетической кривой промежуточного продукта и проанализируем, от каких факторов зависят высота максимума и время достижения максимума.

В точке максимума первая производная уравнения кривой равна нулю

.

.

Отсюда можно получить следующее выражение для времени максимума:

, где .

Теперь можно найти и максимальную концентрацию промежуточного вещества.

.

Преобразуем показатели степени, учитывая, что

.

П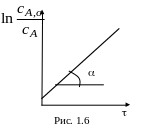 роанализировав полученные координаты максимума на кинетической кривой промежуточного вещества, можно сделать вывод, что высота максимума не зависит от абсолютных значений констант скоростей стадий, а зависит лишь от их соотношения. С ростом отношения максимум на кривой смещается к началу координат и становится ниже.

Константу скорости первой стадии найдем путем линеаризации экспериментальных данных по первой стадии (рис. 1.6).

.

Константу скорости второй стадии найдем из соотношения

.