1. Химическая кинетика

1.1. Кинетика простых реакций

Скорость химической реакции в закрытой системе определяется как

,

где  глубина химической реакции; V  объем реакционной системы;   время.

При постоянном объеме системы скорость реакции равна

,

где  стехиометрическое число компонента k, по изменению концентрации с_k которого определяют скорость. Если компонент k −исходное вещество, то стехиометрическое число равно стехиометрическому коэффициенту, взятому с минусом. Если компонент k − продукт реакции, то стехиометрическое число берется равным стехиометрическому коэффициенту.

Зависимость скорости простой гомогенной реакции от концентрации исходных реагентов определяется при помощи основного постулата химической кинетики, или закона скорости, или закона действующих масс для кинетики.

Запишем основной постулат химической кинетики для односторонней реакции, протекающей в закрытой системе при постоянстве температуры согласно уравнению

,

где A и B  реагенты (исходные вещества); С  продукт реакции.

,

где k − константа скорости реакции; − частные порядки реакции по компонентам A и B.

В случае простых реакций значения частных порядков реакции совпадают со значениями соответствующих стехиометрических коэффициентов (или иногда говорят, что порядок реакции и молекулярность совпадают):

.

Простые гомогенные реакции могут иметь либо первый, либо второй и очень редко третий порядок.

В табл. 1.1 приведены дифференциальные и интегральные кинетические уравнения реакций разных порядков, причем для реакций второго и третьего порядков рассматриваются частные случаи, когда начальные концентрации веществ одинаковы.

Таблица 1.1

Порядок реакции	Дифференциальное кинетическое уравнение	Интегральное кинетическое уравнение
1
2
3

Если известно, что кинетика какой-то исследуемой реакции подчиняется целочисленному порядку (первому, второму или третьему), то экспериментально полученные данные о концентрации вещества в разное время (кинетические кривые) нужно привести к зависимости от времени ; или . Данные зависимости уже не являются кинетическими кривыми, это линейные анаморфозы кинетических кривых. Они будут представлять прямую линию на графике, построенном в координатах, которые следуют из интегрального кинетического уравнения нужного порядка реакции.

Для характеристики реакционных процессов часто используют понятие время полупревращения  время, необходимое для превращения половины исходного количества реагирующего вещества. Математическое выражение для времени полупревращения находят, подставляя в интегральные уравнения реакции разных порядков значения плотности глубины, равной . Выражения времени полупревращения исходного вещества для реакций различных порядков (для реакции второго и третьего порядков рассматриваются равные начальные концентрации веществ) приведены ниже.

Выражение времени полупревращения в реакциях разного порядка

Порядок Уравнение

1

2

3

В реакциях первого порядка время полупревращения не зависит от концентрации исходного вещества, в реакциях второго и третьего порядков  зависит. Следовательно, без всяких расчетов можно сделать вывод о первом порядке исследуемой реакции, если время полупревращения исходного вещества в ней не зависит от начальной концентрации.

Зависимость константы скорости реакции от температуры определяется уравнением Аррениуса

.

Оно содержит два параметра, характеризующих химическую реакцию:  предэкспоненциальный множитель, который не зависит от температуры, и E_а  энергия активации. Энергия активации для большинства реакций также не зависит от температуры.

Энергию активации можно определить, измерив константу скорости при двух значениях температуры. Из уравнения Аррениуса следует

.

Более точно энергию активации определяют по значениям константы скорости при нескольких значениях температуры (рис. 1.1).

Для этого представляют экспериментальную зависимость логарифма константы скорости от обратной температуры в линеаризованной форме:

.

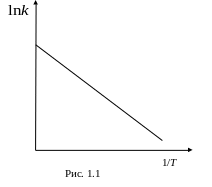В таком случае угловой коэффициент прямой будет .

При рассмотрении кинетики сложных реакций делается допущение о том, что все элементарные реакции (стадии), составляющие сложную реакцию, протекают независимо друг от друга.