3.3. Частная теорема о повторении опытов. Теорема я. Бернулли

При практическом применении теории вероятности приходится встречаться с задачами, в которых требуется определить вероятность любого заданного числа появлений события в результате серии опытов.

В большинстве случаев эти задачи решаются, когда опыты являются независимыми. Несколько опытов называются независимыми, если вероятность того или иного исхода каждого из опыта не зависит от того, какие исходы имели другие опыты.

Независимые опыты могут проводиться при одинаковых или различных условиях Q . В первом случае вероятность события A во всех опытах одна и та же. Во втором случае вероятность события A от опыта к опыту меняется. К первому случаю относится частная теорема, а ко второму - общая теорема о повторении опытов.

Теорема 3.3. (теорема Я. Бернулли). Если производится n независимых опытов, в каждом из которых событие A появляется с вероятностью p, то вероятность того, что событие A появится ровно m раз в n опытах, выражается формулой:

,

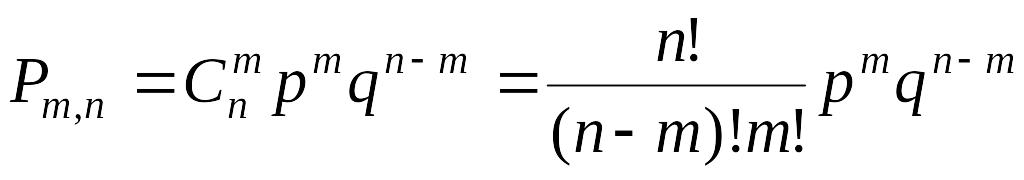где q = 1– p.

Проведем доказательство этой формулы по методу индукции. Пусть производится n = 2 опытов, в каждом из которых может появиться или не появиться некоторое событие A . Вероятность появления события A в каждом опыте равна p , а вероятность не появления q = 1– p. Требуется определить вероятность p того, что событие A в этих двух опытах появится ровно m = 1 раз.

Рассмотрим событие B , состоящее в том, что событие A появится в n = 2 опытах ровно m = 1 раз. Это событие может произойти в двух несовместных случаях:

– событие A происходит в первом опыте и не происходит во втором,

– событие A происходит во втором опыте и не происходит в первом.

Следовательно, событие B можно представить как сумму двух несовместных событий В = + . Учитывая, что события, входящие в произведения событий, несовместны, по теоремам сложения и умножения независимых событий получим:

P(B) = p(1 – p) + (1 – p)p = pq + qp = 2 p q = p q

Рассмотрим теперь n = 3, m = 2. Событие B может произойти в трех случаях:

– событие A происходит в первом и во втором опыте и не происходит в третьем.

– событие A происходит в первом и в третьем опыте и не происходит во втором.

– событие A происходит во втором и в третьем опыте и не происходит в первом.

Тогда B = + + и вероятность появления события A – m = 2 раза в n = 3 опытах будет равна

P(B) = pp(1 - p) + p(1 - p)p + (1 - p)pp = p q + p q + p q = p q = 3 p q.

Таким образом, в соответствии с методом полной индукции для события B, состоящего в том, что событие A появится в n опытах m раз, имеет место

B = ,

причем в каждое произведение событие A должно входить m раз, а должно входить (n – m) раз. Число слагаемых такого рода равно числу сочетаний по m из n , т.е.

.

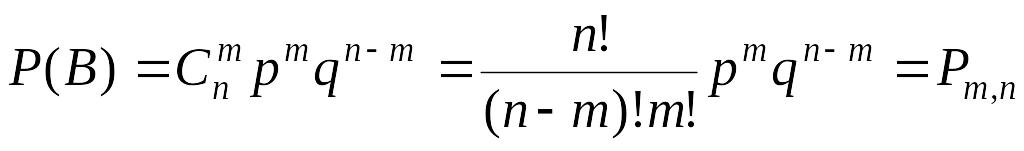Полученную формулу называют формулой Бернулли. Она описывает, как распределяются вероятности между возможными значениями некоторой случайной величины m - числа появления события A при n независимых опытах.

В связи с тем, что вероятности теоремы 2.9 по форме представляют собой члены разложения бинома

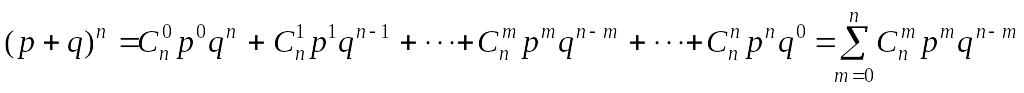
распределение вероятностей теоремы 3.3 называется также биномиальным распределением.

Пример: Оптовая база снабжает 10 магазинов. От каждого магазина независимо от других с вероятностью 0,4 может поступить на очередной

день заявка.

Найти вероятность получения от 10 магазинов четырех заявок.

Решение. В данном случае n = 10, m = 4, p = 0,4. Вероятность получения четырех заявок из десяти согласно формуле Бернулли равна

= 