2.2. Теорема сложения вероятностей совместных событий

Теорема 2.2. Вероятность суммы совместных (произвольных) событий определяется через вероятности произведений этих событий,

взятых по одному, по два, по три и т.д. по формуле

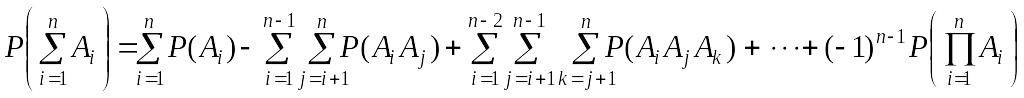
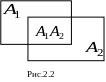
Доказательство. Рассмотрим два совместных события и (рис.2.2). Представим сумму и суммой двух несовместных событий , а событие – суммой двух несовместных событий . Применяя теорему сложения вероятностей для несовместных событий, получим:

P( ) = P( ) + P(( )\( ),

P( ) = P( ) + P(( )\( ).

Отсюда следует, что

P( ) = P( ) + P(( )\( ),

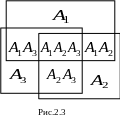
Аналогично вероятность суммы трех совместных событий равна

.

Определим (рис 2.3) вероятность :

.

Следовательно:

.

Таким образом, методом полной индукции для суммы n совместных событий получим формулу теоремы 2.2.

Следствие 1. Если произвольные события, то имеет

место неравенство

.

Действительно, для двух событий

Для трех событий

.

Таким образом, по индукции получим утверждение следствия. Теорема 2.2 позволяет выразить вероятность суммы произвольного числа событий через вероятности произведений этих событий. Аналогично можно выразить произведения произвольного числа событий через вероятности суммы этих событий.

Теорема произведения произвольного числа событий формулируется следующим образом.

Теорема 2.3. Вероятность произведения произвольного числа событий определяется через вероятности суммы этих событий, взятых по одному, по два, по три и т.д. по формуле

+ .

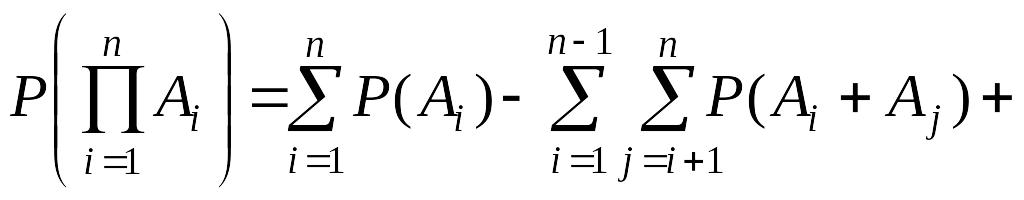
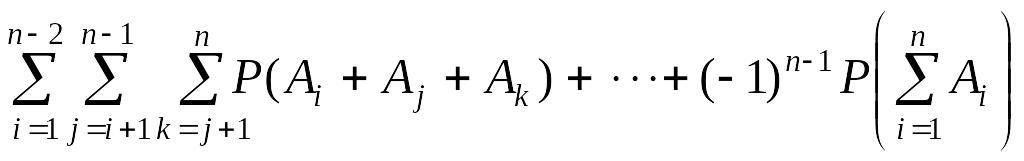Доказательство. Из рассмотрения рис 2.2 видно, что

P( ) = P( ) + P( )  Р( ).

Из рассмотрения Рис 2.3 следует, что

.

Таким образом, методом полной индукции для произведения произвольного числа событий получим формулу теоремы 2.3.

Формулы теорем 2.2 и 2.3 применяются при преобразовании различных выражений, содержащих вероятности сумм и произведений

событий. В зависимости от рассматриваемых задач в некоторых случаях удобно пользоваться только суммами, а в других –только произведениями событий.

Пример: Рассмотрим техническое устройство, состоящее из трех агрегатов (рис 2.4), двух агрегатов первого типа , и одного агрегата второго типа В. Агрегаты , дублируют друг друга. При отказе одного из них происходит автоматическое переключение на другой. Агрегат В не дублирован. Отказ устройства происходит, если отказали оба агрегата , или отказал агрегат В. Таким образом, событие С, при котором происходит отказ устройства представляется в виде С = + В, где – отказ агрегата , – отказ агрегата , В – отказ агрегата В .

Требуется выразить вероятность события С через вероятности событий, содержащих только суммы, а не произведения элементарных событий , и В .

Решение. По формуле теоремы 2.2:

.

Определим по формуле теоремы 2.3 вероятности

P( ) = P( ) + P( )  Р( ),

.

Тогда после несложных преобразований получим:

.

2.3. Теорема умножения вероятностей

Прежде чем излагать теорему умножения вероятностей, введем ряд определений.

Вероятность события A , вычисленная при условии, что имело место событие B , называется условной вероятностью события A и обозначается P(A|B).

Событие A называется независимым от события B , если вероятность события A не зависит от того, произошло событие B или нет. Условие независимости события A от B записывается в виде P(A|B)=P(A).

Событие A называется зависимым от события B , если вероятность события A меняется в зависимости от того, произошло событие B или нет.

Условие зависимости события A от B записывается в виде P(A|B)  P(A).

Теорема 2.4. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.

P(AB) = P(A)P(B|A)

n

Докажем теорему для схемы случаев. Пусть возможные исходы опыта сводятся к n случаям, которые для наглядности изображены на рис.2.5 в виде n точек. Из n случаев событию A благоприятны m случаев, событию B благоприятны k случаев, событию AB благоприятны r случаев. Тогда (рис 2.5)

P(A) = m/n , P(AB) = r/n

Вычислим P(B|A). Если событие A произошло, то из m случаев события A r случаев благоприятствовали событию B.

Следовательно: P(B|A) = r/m

Подставляя значения вероятностей в формулу теоремы 2.4, получим тождество. Теорема доказана.

Следствие 1. Если событие A не зависит от события B, то и событие B не зависит от A.

Доказательство. Если A не зависит от B , то по определению независимости событий

P(A) = P(A|B)

В соответствие с теоремой умножения вероятностей

P(AB) = P(A)P(B|A) = P(B)P(A|B)

Принимая во внимание, что P(A) = P(A|B), из последнего соотношения получим

P(B) = P(B|A).

Из следствия 1 вытекает, что зависимость или независимость события всегда взаимны. Таким образом:

Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.

Понятие независимости событий может быть распространено на случай произвольного числа событий. Несколько событий называются независимыми, если вероятность любого из них не зависит от появления любой совокупности остальных.

Следствие 2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

Р(А В) = Р(А )Р(В).

Следствие вытекает непосредственно из определения независимых событий. Действительно

P(AB) = P(A)P(B|A) = P(B)P(A|B)

Теорема умножения вероятностей обобщается на случай произвольного числа событий.

Теорема 2.5. Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность следующего по порядку события вычисляется при условии, что все предыдущие имели место:

.

Доказательство проводится методом полной индукции:

и т.д.

Теорема 2.6. Вероятность произведения независимых событий равна произведению вероятностей этих событий:

.

Доказательство проводится методом полной индукции

и т.д.

Пример: В урне (рис.2.6) 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Найти вероятность того, что оба шара белые.

Р ешение. Обозначим через А - появление двух белых шаров. Событие А представляет собой произведение двух событий А = , где – появление белого шара при первом вынимании, – появление белого шара при втором вынимании. По теореме умножения вероятностей

.

Пример: Те же условия, что и в предыдущем примере, но после первого вынимания шар возвращается обратно в урну и шары перемешиваются.

Решение. В данном случае события , и , независимы и

Р(А) = = 2/5  2/5 = 0,16.