Полная группа событий
События
образуют полную группу событий в опыте,
если:
они попарно несовместны:
хотя бы одно из событий в опыте произойдет:
Свойство событий, образующих полную группу
Если события образуют полную группу событий, то вероятность их суммы равна 1.
Р( ) = Р( ) =1
Свойства вероятности:
Вероятность достоверного события равна 1.
Р( ) =1
,
m=n
Вероятность невозможного события равна 0.
Р(
)=
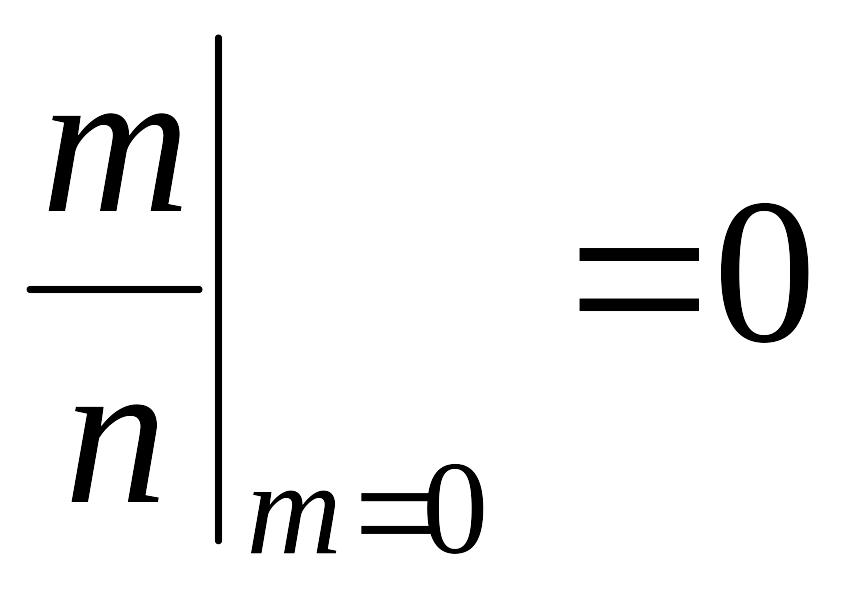
0<P(A)<1 – вероятность случайного события – правильная дробь и она находится в промежутке (0;1).
Геометрическое определение вероятности
Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят понятие геометрической вероятности – вероятности попадания точки в область (отрезок (рис.1.7)), часть плоскости ((рис.1.8) и т.д.).
П
усть
отрезок длиной l
составляет часть отрезка L
. На отрезок L
наудачу поставлена точка. Это означает
выполнение следующих предположений.
Поставленная точка может оказаться в
любой точке отрезка L,
вероятность попадания точки на отрезок
l
пропорциональна длине этого отрезка и
не зависит от его (рис.1.7) расположения
относительно отрезка В этих предположениях
вероятность события A
попадания точки на отрезок l
определяется равенством P(A)
=
.
А
налогичное
рассуждение имеет место и для плоских
фигур. Пусть на область G
(рис.1.8) наугад поставлена «точка».
Требуется определить какова вероятность
того, что она попадет в область q,
являющуюся частью области G.
Множества G
и q
содержат бесконечное множество точек.
Однако «вместимость» множества G
больше «вместимости» множества
q
во столько раз, во сколько площадь
области G
превышает площадь
области
q.
Поэтому естественно считать, что искомая
вероятность равна
.
Приведенные определения являются частными случаями общего определения вероятности. Если обозначить меру (длину, площадь, объем) области через mеs , то вероятность попадания точки, поставленной наугад (в указанном выше смысле) в область d – часть области D , равна
.
Следует отметить, что в случае классического определения вероятности, если вероятность достоверного (невозможного) события равна единице (нулю), справедливы и обратные утверждения. Например, если вероятность события равна нулю, то событие невозможно. При геометрическом определении вероятности обратные утверждения имеют место не всегда. Например, вероятность попадания поставленной наугад точки в одну определенную точку области D равна нулю, однако это событие может произойти, т.е. не является невозможным.
Аксиоматическое определение вероятности
Аксиомы Колмогорова
А1: Не отрицательность вероятности: каждому событию А соответствует неотрицательное число Р(А).
А2: Нормировка вероятности: вероятность достоверного события равна 1.
Р( ) =1
А3: Конечная аддитивность вероятности: для любых несовместных событий А и В
Вероятность суммы Р(А+В) равна сумме вероятностей этих событий Р(А)+Р(В).
Определение вероятности по Колмогорову:
Вероятностью события А называется функция Р(А), удовлетворяющая аксиомам (А1-А3)