Квантиль

Определение 1. Квантилью уровня p функции распределения F(x) СВ X называется минимальное значение x, при котором функция распределения F(x) не меньше p, т.е. , что показано на рис. 13.1.

Замечание 1. Если функция распределения строго монотонна и непрерывна, то квантиль является единственным решением уравнения F(x_p) = p, а по квантили x_p однозначно определяется вероятность p.

Определение 2. Квантиль уровня p = 1/2 называется медианой.

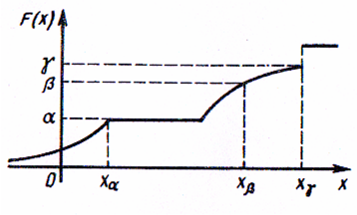
Рис. 13.1

Замечание 2. Если плотность распределения существует и симметрична относительно нуля, то x_p = -x_1-p.

Замечание 3. Квантиль, наряду с уровнем значимости p, является одной из основных статических характеристик, используемых в математической статистике.

Тема 7. Случайные последовательности и их сходимость Лекция 14 Виды сходимости последовательностей случайных величин

Пусть на вероятностном пространстве определены случайные величины со значениями

1. Говорят, что последовательность сходится по вероятности к , если

. (14.1)

Обозначим сходимость к по вероятности в виде .

2. Говорят, что последовательность с х о д и т с я к п о ч т и н а в е р н о е (с вероятностью единица, почти всегда, почти всюду на , mod ), если

. (14.2)

Здесь

. (14.3)

Обозначим эту сходимость в виде .

3. Говорят, последовательность сходится к в среднем квадратическом, если:

. (14.4)

Сходимость к в среднем квадратическом обозначают или .

4. Говорят, что последовательность сходится к по распределению с обозначением , если

. (14.5)

Здесь , - функции распределения и , причем сходимость к подразумевается для всех , за исключением, может быть, точек разрыва .

Теорема 14.1. Сходимости к , введенные определениями 1 – 4, связаны между собою отношениями, показанными на рис.14.1:

Рис.14.1.

Докажем вначале, что . Для этого рассмотрим события , , . Очевидно, что , где - множество элементарных событий, в котором не сходится к при . В самом деле, пусть , . Тогда если , то .

Отсюда , следовательно, , .

Таким образом,

.

Из правой части этой эквивалентности как раз и следует, что .

По определению сходимости почти наверное имеем:

. (14.6)

Отсюда и из условия находим . Событие есть предел невозрастающей последовательности событий .

Поэтому по аксиоме непрерывности

. (14.7)

Поскольку , то .

Отсюда, учитывая (14.7), найдем:

.

Последнее выражение, будучи справедливым для произвольного , означает, что имеет место .

Перейдем к доказательству .

Пусть , то есть имеет место (14.4). Записывая неравенство Чебышева для случая , получим:

.

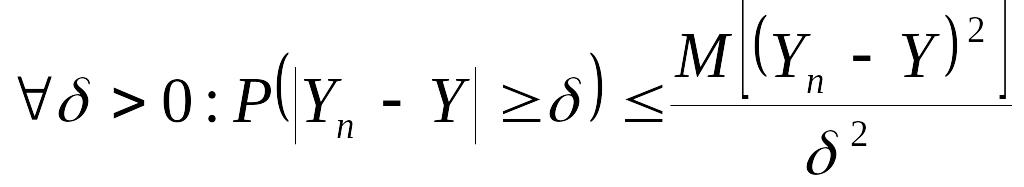Поскольку правая часть этого неравенства по условию стремится к нулю при , то в левой части его при имеем предел, равный нулю. Но это есть .

Докажем теперь предложение .

Пусть , т.е. выполнено условие (14.1). Зафиксируем произвольное . Тогда

. (14.8)

Очевидно, что

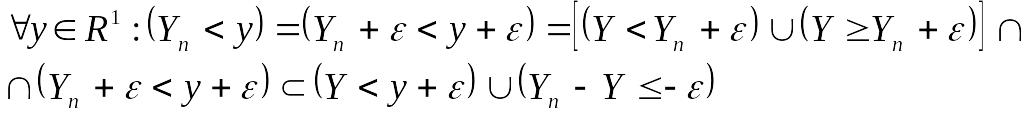
Отсюда имеем:

. (14.9)

Поскольку , то из (14.9) следует

.

Отсюда, принимая во внимание условие (14.8), найдем:

. (14.10)

Здесь и – функции распределения и .

Очевидно также, что

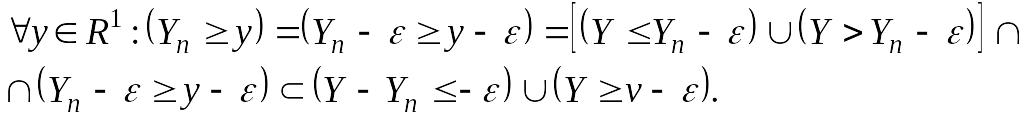
Отсюда следует

.

Таким образом,

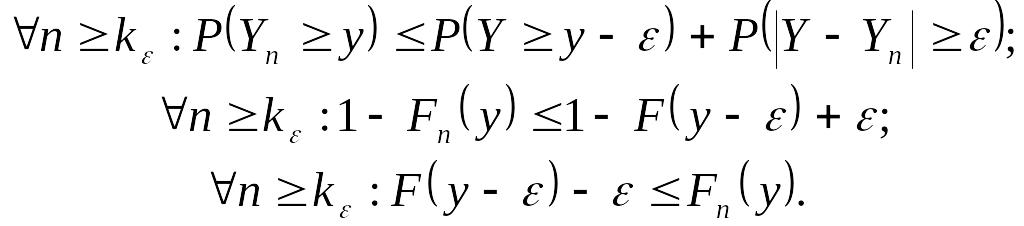(14.11)

Объединяя (14.10) и (14.11), найдем

. (14.12)

Пусть - точка непрерывности . Тогда для любого и сколь угодно малой имеем:

,

т.е. .

Отсюда и из неравенства (14.12) для всех начиная с достаточно большого номера будем иметь:

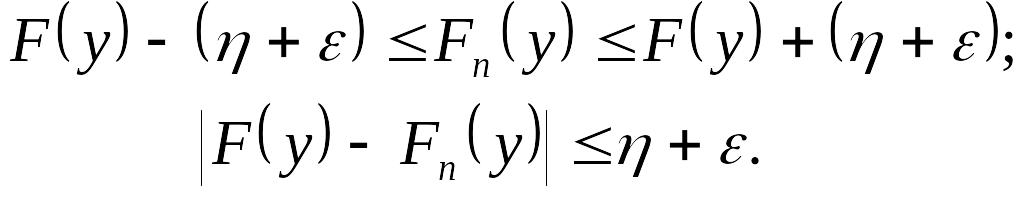
Поскольку здесь произвольна, а сколь угодно мала, то последнее предложение означает, что в точках непрерывности имеем при . Но это означает .

Теорема 14.2.

. (14.13)

Доказательство. Из условия следует:

. (14.14)

Здесь - функция распределения .

Из условия находим:

. (14.15)

Здесь - функция распределения .

Из (14.15) следует:

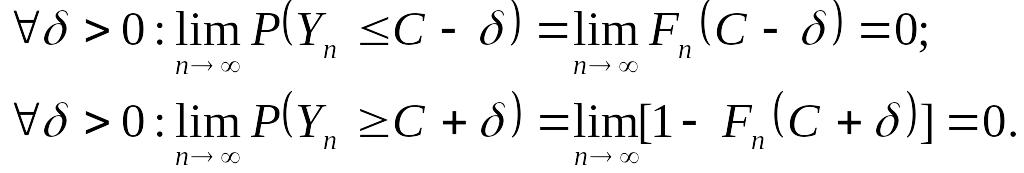(14.16)

Поскольку

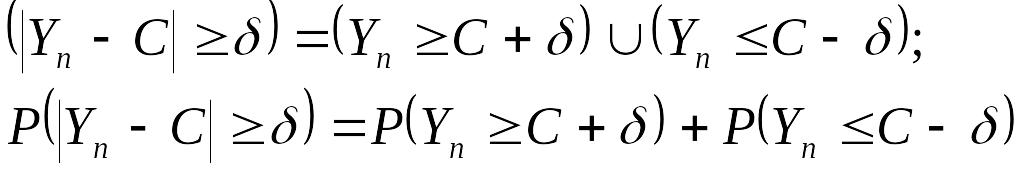
то, учитывая соотношения (14.16), найдем:

Следующая теорема решает вопрос о сходимости последовательности значений функции, соответствующих элементам сходящейся по вероятности последовательности случайных величин. Эта теорема, в частности, имеет важные применения в математической статистике.

Теорема 14.3. Если - непрерывная функция и , то .

Доказательство. Всегда можно найти , такое, что

. (14.17)

Поскольку на всякая непрерывная функция равномерно непрерывна, то для выбранных и имеем:

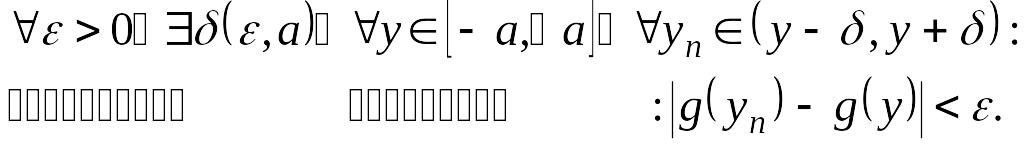(14.18)

Рассмотрим теперь события:

, , .

Из условия (14.18) следует:

Отсюда имеем:

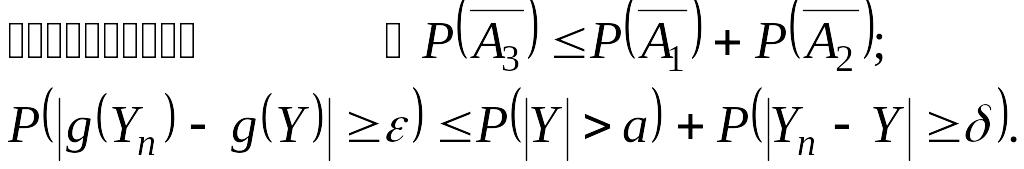(14.19)

По условию , поэтому для всех достаточно больших имеем:

.

Теперь, учитывая (14.17) вместо (14.19) получим:

.

Заметим, теорема справедлива и в случае, когда представляет собою непрерывную функцию более чем одного аргумента. Например, если - непрерывная функция двух аргументов, то

. (14.20)

Теорема 14.4. Пусть а) последовательность сходится по распределению к случайной величине с функцией распределения , б)последовательность сходится по вероятности к постоянной величине . Тогда последовательность , где 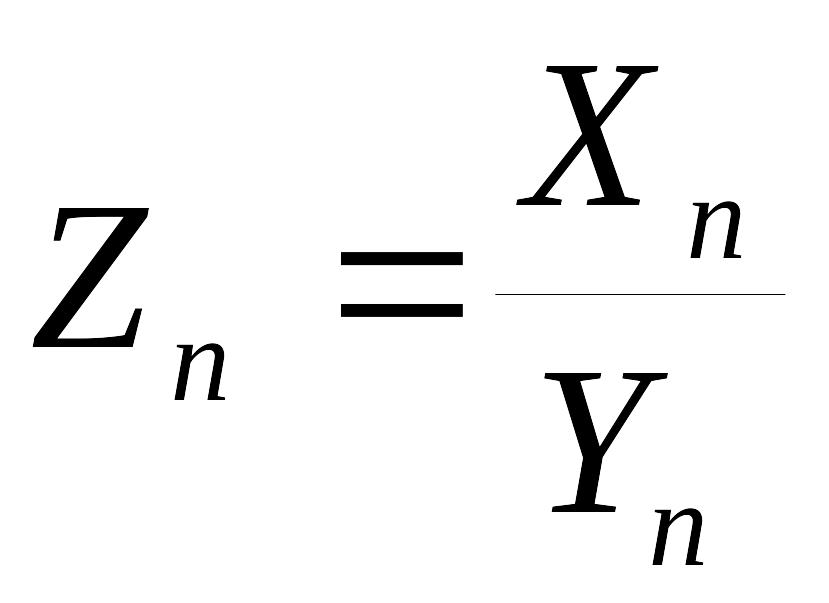, сходится по распределению к случайной величине с функцией распределения .

Для доказательства теоремы запишем вначале соотношения, справедливые при сколь угодно малых :

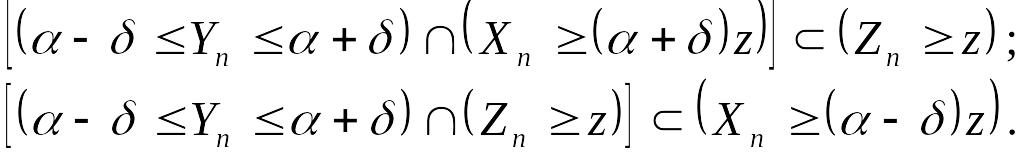(14.21)

Очевидность их при достаточно малых видна из рис.14.2.

Рис.14.2

Здесь области с горизонтальной и вертикальной штриховкой обозначают соответственно события и .

Из соотношения (14.21), учитывая закон контрапозиции математической логики и соотношения двойственности теории множеств, получим:

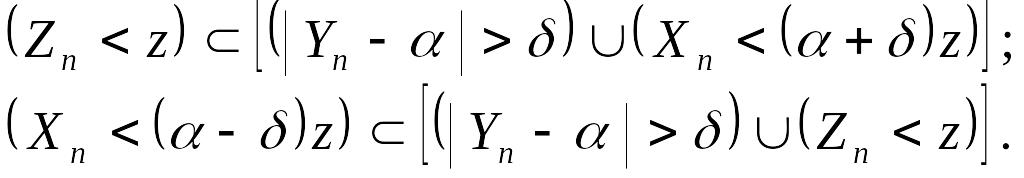
Теперь можно записать:

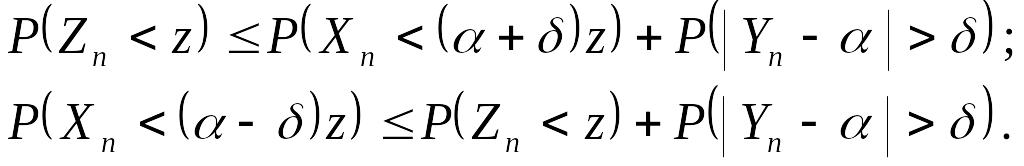
Следовательно,

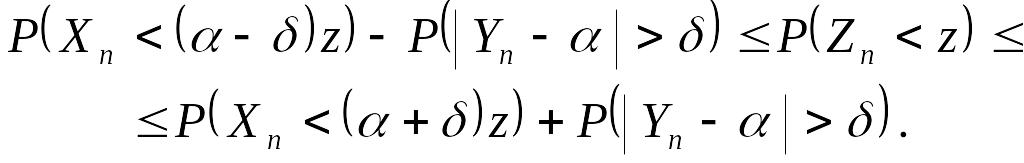(14.22)

По условию б) теоремы имеем:

. (14.23)

Поскольку всякая функция распределения имеет не более чем счетное множество точек разрыва, то для любой точки всегда можно найти сколь угодно близкие к ней точки и , в которых непрерывна. Поэтому по условию а) теоремы имеем:

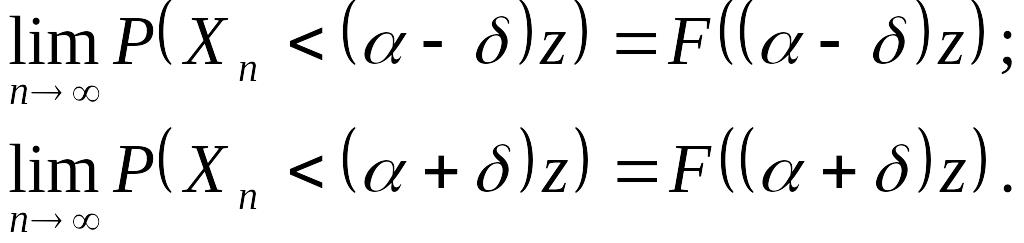(14.24)

Из соотношений (14.22)-(14.24) теперь находим:

.

Если - точка непрерывности , то

.

Отсюда

.